[수학] 컴퓨터와 수학 // 4색문제와 케플러의 추측

한동안 너무 계산거리들만 집중적으로 올린 것 같아서 조금 쉬어가자는 의미에서 이번 포스팅을 준비해 보았습니다. 요즘에는 공학, 자연과학 아니 거의 전반 분야에서 컴퓨터를 이용한 계산들을 많이 쓰곤 합니다. 그래서 특별히 컴퓨터와 수학이라는 제목으로 수학 난제 중 컴퓨터의 도움으로 해결한 두 문제를 소개하려고 합니다. 바로 4색 정리 와 케플러의 추측 문제를 다루어 볼까 합니다.

4색정리

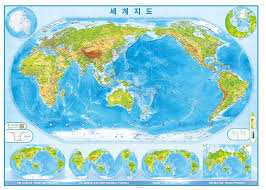
위 지도를 보면 여러 나라들이 나오는데요, 인접한 나라끼리 서로 색을 칠하는데 여기에 필요한 색이 몇가지면 될까 하는 문제입니다. 좀 더 엄밀하게 말해 2차원내의 모든 평면 지도는 최소한 몇가지의 색으로 다 칠할 수 있겠냐는 것을 물어보는 문제입니다. 문제 자체는 엄청 간단합니다.

일단 이런 도형을 가정해 볼까요

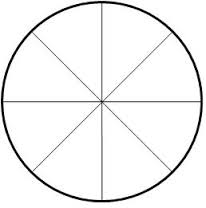
일단 당연히 한가지 색이면 안되겠죠

색이 두가지인 경우 A,B, A,B,A,B,A,B (시계 혹은 반시계로 칠하면 됩니다) 로 쪼개면 색을 칠할 수 있죠.
그런데 만약에 홀수개로 쪼개진다면 2가지 색으로 전체를 다 구분 할 수 없게 되어 버립니다. (연속으로 겹치는 색이 존재하게 됩니다 ) 이럴 때에는 3개만 있으면 충분하죠.

하지만 가운데에 구멍이 뚤려있다면? 이럴 때에는, 가운데에 색칠해야 되는 원이 있고 그 나머지 부분이 짝수개로 쪼개지면 3개 색으로 충분하지만 홀수개로 쪼개지면 4개가 필요합니다, 이렇듯 어떤 구조, 다이어그램을 가지느냐에 따라 최소한의 색이 달라집니다

---

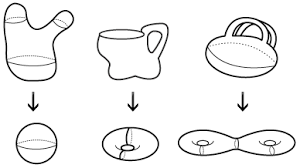
이런 문제를 일반화 하는 과정을 통해 위상수학은 많이 발전하게 됩니다. 흔히 말하는 이산수학의 개념들도 이때 많이 연구 된 것으로 압니다. 우리에게 잘 알려진 것으로는 다이어그램과 네트워크 이론, 오일러의 정리 등이 있습니다.

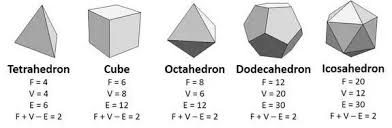
[ 그림출처 ]

6색 문제의 경우 오일러의 정리, v-e+f=2와 네트워크 이론을 이용하면 쉽게(?) 증명할 수 있고 5색 문제도 증명하는데 그리 오래 걸리지 않았다고 합니다. 문제는 바로 4색이었죠. 4가지 색으로 평면의 경계를 구분할 수 있을 것이냐

1976년 일리노이 대학교의 Appel 과 Haken 이 4가지 색으로 충분하다는 것을 증명하였습니다. 그들은 2차원 지도를 그 특징에 따라 1482개의 경우로 분류하고 대략 천여 시간동안 컴퓨터를 이용하여 모든 경우를 확인 하는 방식으로 이 4색 문제를 증명합니다.

처음에 이 결과가 나왔을 때 컴퓨터를 가지고 모든 경우의 수를 확인한 이런 방법의 증명은 아름답지 않다란 수학자들의 비판이 많았습니다. ㅋㅋㅋㅋ 가능한 모든 경우의 수를 체크하여 확인하였고 해당 과정 속에 반례가 없어 이 정리는 참이다. 이게 이 문제의 증명방법이었으니까요 ㅎㅎ

---

케플러의 추측

이 문제는 3차원 공간에 어떻게 공을 효율적으로 많이 집어넣느냐에 관한 문제입니다.

1611년 케플러는 3차원 공간, 박스에 동일한 크기의 구들을 가장 조밀하게 쌓는 방법은 FCC(Face-centered cubic packing) 즉 면심입방쌓기가 아닐까란 추측을 내어놓습니다.

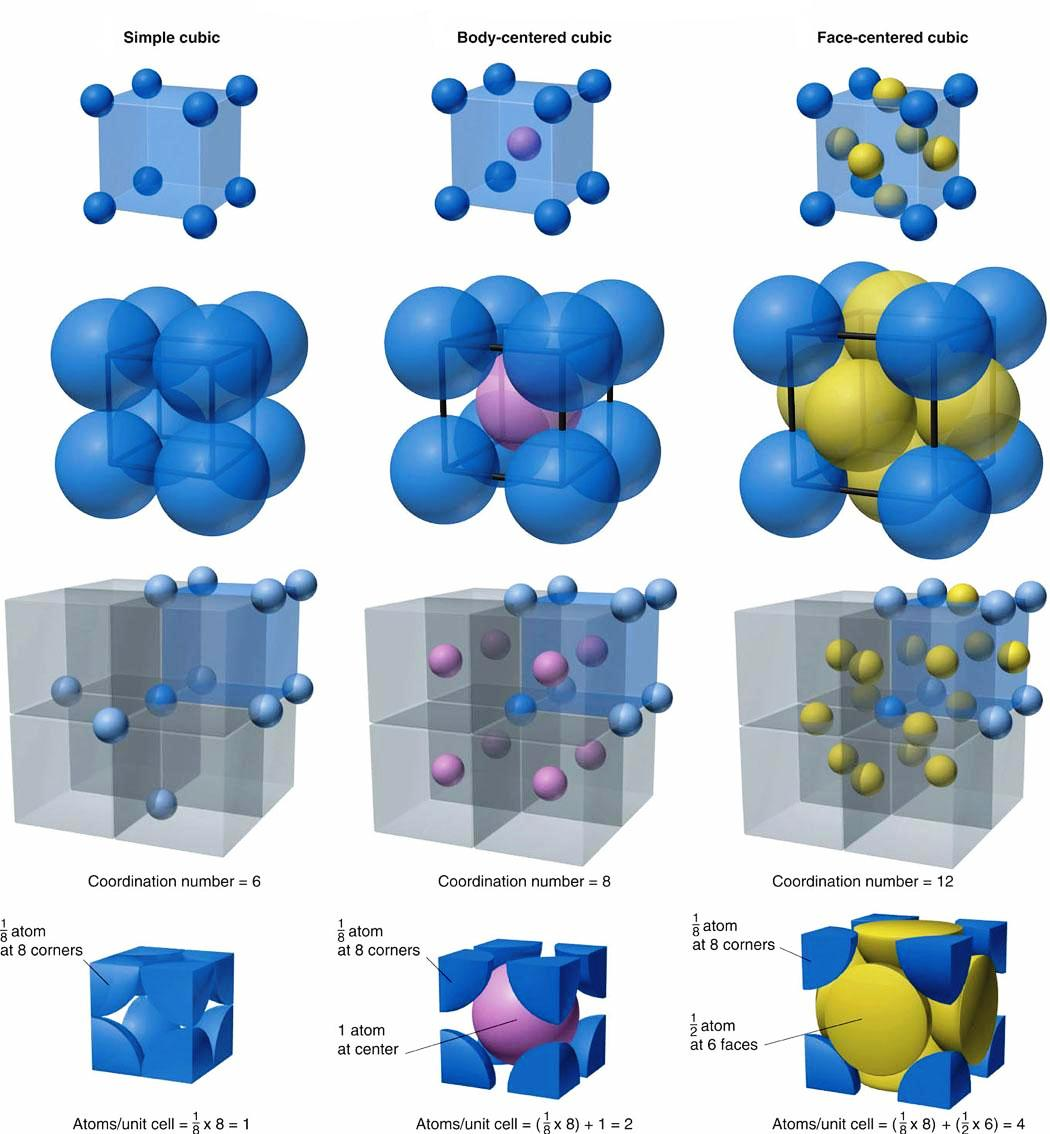
[그림참조, 화학, 재료공학 공부를 하다보면 많이 보게 되는 도형이죠 ㅎㅎ]

후에 2차원의 경우에는 가우스에 의해 해결이 되었는데 3차원의 경우에 따로 증명이 된 것은 없고 추측만 있었을 뿐이었습니다. [하지만 웃기게도 다른 고차원에서의 같은 문제가 풀리게 됩니다. ㅋㅋㅋ 4색 문제 역시 2차원 평면이 아닌 경우 대표적으로 7차원 torus 위에서의 색깔 문제가 풀린 것으로 알고 있습니다. ]

3차원의 경우, 이 문제는 Finite Lattice 위의 최적화 문제로 정의되어 컴퓨터 공학 문제로 바꾸게 됩니다.

여기서 핵심적인 역활을 한 것이 Thomas Hales으로 Linear programming 과 관련된 기법을 이용하여 이 문제를 해결하였다고 합니다만 저도 자세히 알지는 못합니다.

Hales 는 이런 프로젝트를 "Project FlysPeck" 라고 불렀습니다. 최초로 그가 증명한것은 1998년이었고

[이 시리즈의 논문을 통해서 1998년 처음 증명법을 공개 합니다 ]

그 뒤 새로운 증명(?) 을 몇번 더 보여줍니다.

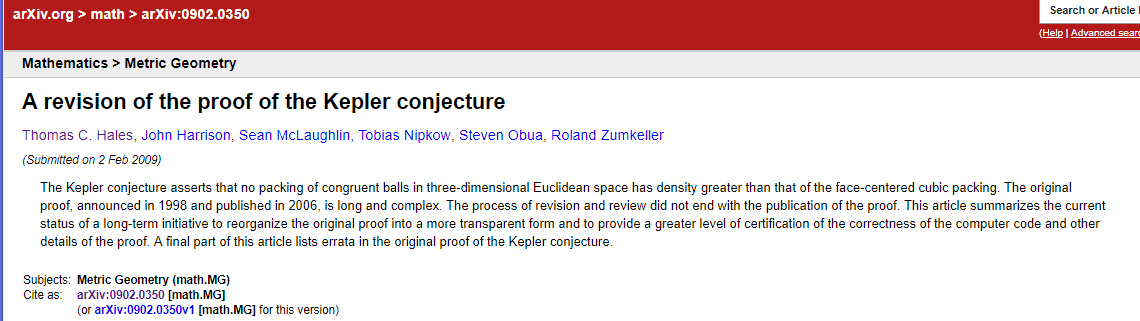
[98년과 2006년에 제공한 증명이 너무 길고 복잡했다고 2009년에 새로 논문을 내신... 이 때는 예전보다 공동연구자가 많아진 것을 볼 수 있습니다]

가장 최신의 케플러 추측과 관련된 Hales 의 논문, 이번엔 훨씬 더 많은 사람들이 참여했죠. 이 논문에서 그가 이끌어 왔던 FlysPeck project 를 드디어 끝을 냅니다.

---

이처럼 현대로 올 수록 컴퓨터와 수학은 빼놓을 수 없는 존재가 되어 버렸습니다. 이런 접근법의 장점은 모든 가능한 경우의 수를 하나씩 확인하여 찾는 것과 엄청난 계산을 통하여 확인하는 것입니다. 예전의 쉬운 모델링 문제들은 충분히 머리로 손으로 해결이 되었지만 수천가지 수만가지의 경우의 수들이 나오는 현대의 문제들은 더 이상 이런 주먹구구식의 접근 방법이 통하지 않아 많은 사람들이 기피하는 방법이 되어 버렸습니다. 하지만 컴퓨터의 출연으로 이런 일종의 노가다 방식의 증명들이 이루어 지고 있습니다. [즉 컴퓨터 코딩 공부를 열심히 합시다 ... ㅎㅎ;; ]

아직도 사색문제나 케플러의 추측 문제들이 수학적으로 증명되지 않았다고 보는 사람들도 있습니다. 이 들에게는 이런 접근법은 수학이 아니고 혹시 한 두개의 반례들이 빠지지 않았나의 가능성을 묻습니다.

여러분들은 이런 컴퓨터를 이용한 증명법에 대해서 어떻게 생각하시나요? ㅎㅎ