CONTEST // ∑∑Remembering MATH∑∑ and first ∑∑Problem#1∑∑
I have long wanted to do a math competition. And this task with its MANY solutions is just for that.
Побачив таку задачку, як каже автор її можна розв'язати багатьма способами, що якраз демонструє те, що не треба знати ВСЮ математику. Я сам наприклад в школі не пам'ятав всіх формул і часто виводив їх під час розв'язуванні задач. Наприклад висота рівностороннього трикутника, чи його площа...
I saw such a problem, as the author says, it can be solved in many ways, which just demonstrates that you do not need to know ALL the math. For example, at school I did not remember all the formulas and often deduced them when solving problems. For example, the height of an equilateral triangle, or its area ...
Увидел такую задачу, как говорит автор её можно решить многеством способов, и это как раз демонстрирует то, что можно и не знать ВСЮ математику. Я сам например в школе не помнил всех формул и часто выводил их при решении задач. Например, высота равностороннего треугольника, или его площадь ...
Давно хотів зробити математичний конкурс. А ця задача з її БАГАТЬМА розв'язками якраз для цього.
Конкурс/ CONTEST Remembering MATH
UA
- Відповіді надсилайте через 24 години, щоб дати змогу іншим, та й собі добре подумати над задачею. Відповідь - просто коментар чи коментар з посиланням на ваш пост-розв'язування задачі розміщуйте коментарем до цього посту.
- Оформлення розв'язування будь-яке: від GeoGebra до аркуша паперу з олівцем чи ручкою.
- Звісно що
требабажана аргументована відповідь, хоч всі були на уроці математики багато років тому. - Пост розмістити в спільноті Steem-BRU (BY-RU-UA), тег #rememberingmath
- У своєму пості запросити одного друга до розв'язку задачі та посилання на пост із задачею.
- Пост будь-якою мовою - головне мова математики.
- Дата проведення з 18.09.2021 по 24.09.2021 включно.
- Винагорода 10 STEEM буде розподілена між учасниками. За повноту, швидкість, оригінальність,...
EN
I have long wanted to do a math competition. And this task with its MANY solutions is just for that.
- Send the answers in 24 hours to allow others and to think well about the task. Answer - just post a comment or a comment with a link to your post-comment task.
- Design any solution: from GeoGebra to a sheet of paper with a pencil or pen.
- Of course,
you needthe desired argumentative answer, although everyone was in math class many years ago.- Post to the Steem-BRU community (BY-RU-UA), tag #rememberingmath
- In your post, invite a friend to solve the problem and link to the post with the problem.
- Post in any language - the main language of mathematics.
- Date from 18.09.2021 to 24.09.2021 inclusive.
- The 10 STEEM rewards will be distributed among the participants. For completeness, speed, originality, ...
RU
Давно хотел сделать математический конкурс. А эта задача с её МНОГИМИ решениями как раз для этого.
- Ответы присылайте через 24 часа, чтобы дать возможность другим, и себе хорошо подумать над задачей. Ответ - просто комментарий или комментарий со ссылкой на ваш пост-решения задачи размещайте комментарием к этому посту.
- Оформление розвязування любое: от GeoGebra к листу бумаги с карандашом или ручкой.
- Конечно что
надожелательно аргументовно ответ, хотя все были на уроке математики много лет назад.- Пост разместить в сообществе Steem-BRU(BY-RU-UA), тег #rememberingmath
- В своем посте пригласить одного друга к решению задачи и ссылку на пост с задачей.
- Пост на любом языке - главное речь математики.
- Дата проведения с 18.09.2021 по 24.09.2021 включительно.
- Вознаграждение 10 STEEM будет распределена между участниками. За полноту, скорость, оригинальность ...
Problem #1
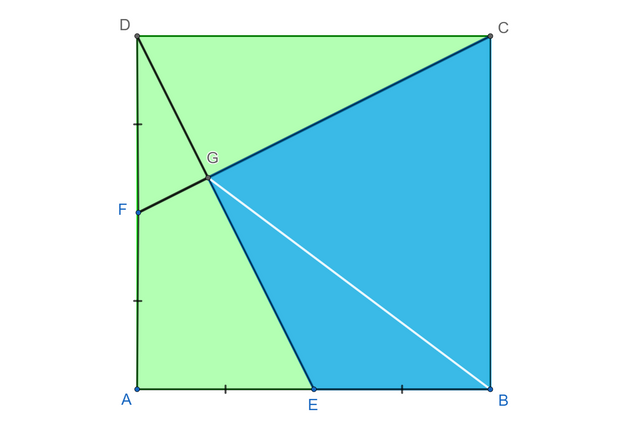
Дано: ABCD квадрат
Точка F серединаAD, точка E середина AB .
Відрізки DE і FC перетинаються в точці G.
а) Знайти довжину GB, якщо квадрат має сторону 10 см.
б) Довести що навколо чотирикутника CBEG можна описати коло.
Given: ABCD square
Point F midAD, point E mid AB.
The segments DE and FC intersect at the point G.
a) Find the length GB if the square has a side of 10 cm.
b) Prove that a circle can be described around the quadrilateral CBEG.
Sorry for the possible incorrect auto translation of mathematical terms
Дано: ABCD квадрат
Точка F серединаAD, точка E середина AB.
Отрезки DE и FC пересекаются в точке G.
а) Найти длину GB, если квадрат имеет сторону 10 см.
б) Доказать что вокруг четырехугольника CBEG можно описать окружность.
А как быть с явными математиками, отнестись построже)))? @allfabeta, @filinpaul, @ir3k
нужно именно математически? (невинный лукавый взгляд)
)))))))))) а как?? сначала чуть под стол не уполз.... а потом, может Вы какой секрет знаете? Я одним способом решил, а дальше..пока не вижу
В принципе любым - я свой задачник хочу сделать, типа избранное))
ну, историю-то о Нильсе Боре и барометре все знают.
так что матеематикам можно дать задание решить НЕ математическим путем.
Вообще же самое очевидное и простое решение это.... напишу после всех ответов))
#ContestAlerts
Этот конкурс включен в ежедневный Активный список конкурсов
👉 Contest Alerts: Active Contest List on 17th September 2021 – Win 2700+ STEEM
Следите за обновлениями и следите за новостями
Оформляю свои два решения в пост.
"Очевидное и простое решение" не буду писать)
Мои два решения длинные, без математической красоты - краткости и лаконичности)
Эти мои два решения немного по Стругацким, вернее, по Акико Ёсано:
"Кривые, глухие окольные тропы..." 😊 😃
очевидное и простое? - я наверное мистер сложность, не скажу что моё решение простое))) Ах да, всё же относительно....
На второй вопрос ответ нашёл быстро, а с первым пришлось топать долго через теорему косинусов. Получив ответ и на него и обнаружив равнобедренные треугольники, стал искать короткое решение, но, блин, не вижу его... Зато нашёл ещё одно длинное. Вопрос: есть короткое решение вообще?
Ага, я тоже - первый способ через теорему косинусов, а второй - через теорему Пифагора)
))))
все узнаем потом))) Надо как-то паузу держать с подсказками)) Да там есть равнобедренный...я без синусов косинусов решал... материал 7го класса, ну разве что описать вокруг четырех угольника окружность обсуждают в восьмом - за вермя работы в школе хоть по классам
полочкамматериал разложила теорема косинусов - девятый, но это не страшно - мне нужно разнообразие решений
последний день сегодня... мне же интересно)))
Ждём результатов конкурса!
И альтернативные решения тоже ждём)
Или я одна приняла участие и забираю всю награду? ))) 😊 😃 😊
Был только один участник!!))) Заочно поздравляю... я же в результатах хочу и своё решение вставить... а всё никак не докажу что он равнобедренный, то репетиторство, то иные посты... вот-вот будет
кстати прошлую задачу с квадратом я так чудно(сложно) решил....
:-))
Понятно. Жду) Уже - завтра - октябрь!
Ах..решил ползадачи, хожу по кругу(( опубликую итог без своего решения, а кто говорил что оно должно быть)) может там на уровне 7го класса и не решить))
Мои два решения, не использующие тот факт, что что треугольник BGC равнобедренный...
https://steemit.com/hive-171319/@ir3k/contest-sum-sum-remembering-math-sum-sum-and-first-sum-sum-problem-1-sum-sum-from-ir3k