Monte Carlo solution for Mathematics × Programming Competition #7 数学 × 程式编写比赛 (第七回) 蒙特卡罗撒点

@kenchung 's Contest #7 is fun. You can check the math solution from @tvb 's post

Bruteforce is the first programming approach that comes to my mind. It is easy to implement and straightforward. One thing to keep in mind is that the point cannot fall exactly on the edge of the square. The coordinates of x and y are incremented by a small number e.g. x+= 1e-5, y += 1e-5.

It is not exactly the bruteforce.. because you just can't simply bruteforce all points... We call it sampling bruteforce where you iterate nearly as many points as possible by a resolution.

Then the answer is just by counting all the valid points divided by total number of points (sampling)

To check if a point is valid, we can just connect (x, y) to four corners, and check these 4 triangles one by one. We need a cosine formula that computes the angles given three 3 sides.

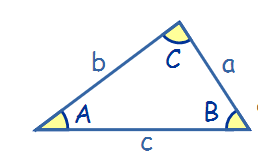
Image from: https://www.mathsisfun.com/algebra/trig-cosine-law.html

Known 3 sides, we use formula c2 = a2 + b2 − 2ab cos(C) to compute the cos values for 3 angles. Then you can compute the angle (in degrees) using the arc-cosine function. Alternatively, we can check the cos(angle) value larger than -0.5 because cos(120 degrees) = -0.5.

The following computes the side given 2 points:

function getSide(x1, y1, x2, y2) {
    return Math.sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2))
}

To check if a triangle has angles smaller or equal to 120 degrees.

function check(x1, y1, x2, y2, x3, y3) {
    var a = getSide(x1, y1, x2, y2);
    var b = getSide(x1, y1, x3, y3);
    var c = getSide(x2, y2, x3, y3);
    var cosc = (a * a + b * b - c * c) / (2 * a * b);
    var cosa = (b * b + c * c - a * a) / (2 * b * c);
    var cosb = (c * c + a * a - b * b) / (2 * c * a);
    return (cosc >= -0.5) && (cosb >= -0.5) && (cosa >= -0.5);
}

If you use Math.acos, the third angle can be computed by 180-A-B.

function check(x1, y1, x2, y2, x3, y3) {
    var a = getSide(x1, y1, x2, y2);
    var b = getSide(x1, y1, x3, y3);
    var c = getSide(x2, y2, x3, y3);
    var cosc = (a * a + b * b - c * c) / (2 * a * b);
    var cosa = (b * b + c * c - a * a) / (2 * b * c);
    angle_c = Math.acos(cosc);
    angle_a = Math.acos(cosa);
    angle_b = 180 - angle_c - angle_a;
    return (angle_c <= 120) && (angle_b <= 120) && (angle_a <= 120);
}

Now, the bruteforce sampling...

var total = 0;  // Total sampling points
var valid = 0;  //Valid points

for (let x = 1e-7; x <= 0.99999; x += 1e-4) {
    for (let y = 1e-7; y <= 0.99999; y += 1e-4) {
        total ++;
        if ( check(x, y, 0, 0, 0, 1) &&
            check(x, y, 0, 1, 1, 1) &&
            check(x, y, 1, 1, 1, 0) &&
            check(x, y, 1, 0, 0, 0)         
        ) {
            valid ++;
        }
    }
}

console.log(valid);
console.log(total);
console.log(Math.round(valid / total * 1000) / 1000);  // 3 decimal precisions.

The precison for 3 decimal places remain unchanged from incremental step 1-3 to 1e-6 at the cost of incrementing computational resources.

This method is deterministic i.e. if you run the program many times, you will still get exactly same output (answer).

The runtime complexity is O(xy) where x and y are the incrementing steps for x and y coordinate. How about we just want to know roughly probability (we don't need to know the 4-th or 5-th decimal precisionn)?

We can use the following Monte Carlo random sampling method. If we have enough sampling points, the probability will be very close to the actual answer.

const N = 10000000;

for (let i = 0; i < N; ++ i) {
    let x = Math.random(1.0);  // return  [0, 1)
    let y = Math.random(1.0);
    if ( check(x, y, 0, 0, 0, 1) &&
        check(x, y, 0, 1, 1, 1) &&
        check(x, y, 1, 1, 1, 0) &&
        check(x, y, 1, 0, 0, 0)         
    ) {
        valid ++;
    }
}

console.log(valid);
console.log(N);
console.log(Math.round(valid / N * 1000) / 1000);

Please note that Math.random(1.0) returns [0, 1) where 0 is inclusive, but the error may be negible because this entire method is based on random sampling, which has slight errors!

Even if you have 0.213 as answer, the valid points count may vary a little bit:

2126142
2127333
2125929
....

So, if you have a small N, the output answer may not be good enough which may be 0.212, 0.214 (the close numbers). The runtime complexity is O(N) where N is the number of sampling points.

If you need a quick answer which may not be that accurate, you may give a N=1e4 where it may output 0.200, 0.205, 0.216, 0.215 ... which is roughly 20%. The advantage is quick running time.

However, by incrementing N, you can run it in parallel, either distributed or multithreading/multicores. Using the C++ Parallel For, we might have such implementation.

int main() {
    srand(time(NULL)); // seed
    const int N1 = 1000;
    const int N2 = 100000;
    int n = 0;
    int c = 0;
    Concurrency::critical_section cs;
    Concurrency::parallel_for(0, N1, [&](int i) { // Parallel For
        int t = check(N2);  //  Parallel Blocks
        cs.lock(); // Race Conditions
        n += N2;   // Total Sampling points
        c += t;    // Total Valid Points
        cs.unlock();
    });
    cout < < "Probability ~= " << setprecision(9) << (double)c / n  << endl;
    return 0;
}

The Monte Carlo and the 'Sampling' bruteforce methods are all based on sampling..

Designed by @nicolemoker

@tvb 在她的方案中 讲了的数学方法需要用到各种三角公式来计算面积，我数学功底不行，这种方法对我来说太麻烦（虽然算面积这种想法我也想到了）。

暴力，我想大家都会首先想到，而且程序好写，需要注意的一点就是你起始点不能在正方形边上，然后 x 和 y 坐标 都以一个非常小的 步长 增量，比如 x += 1e-5, y += 1e-5。

补一句：这里的暴力并不是真的暴力，因为你无法穷举所有的点，这里只是尽可能的穷举“所有”，有一点小误差。

这样一来，程序的思路就非常明确了，只需要判断一下是否是有效点，然后统计一下除于总个数就是概率。

判断逻辑也较为简单，根据 (x, y) 连接四个点，然后得到4个三角形，依次对每个三角形进行判断内角，这里我们需要用到一个三角公式。

图片来自：https://www.mathsisfun.com/algebra/trig-cosine-law.html

已知 三边长，可以通过 公式: c2 = a2 + b2 − 2ab cos(C) 来推导三个角的 cos 值，然后你可以 反余玄来获取角度，但也可以直接 判断 是否大于 -0.5。因为 cos(120度)=-0.5，余玄值若是大于 -0.5 则角度小于 120度。

假设给定两个点的坐标，我们算出边长：

function getSide(x1, y1, x2, y2) {
    return Math.sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2))
}

所以判断逻辑为：

function check(x1, y1, x2, y2, x3, y3) {
    var a = getSide(x1, y1, x2, y2);
    var b = getSide(x1, y1, x3, y3);
    var c = getSide(x2, y2, x3, y3);
    var cosc = (a * a + b * b - c * c) / (2 * a * b);
    var cosa = (b * b + c * c - a * a) / (2 * b * c);
    var cosb = (c * c + a * a - b * b) / (2 * c * a);
    return (cosc >= -0.5) && (cosb >= -0.5) && (cosa >= -0.5);
}

如果你是用 Math.acos 算出角度，可以变成：

function check(x1, y1, x2, y2, x3, y3) {
    var a = getSide(x1, y1, x2, y2);
    var b = getSide(x1, y1, x3, y3);
    var c = getSide(x2, y2, x3, y3);
    var cosc = (a * a + b * b - c * c) / (2 * a * b);
    var cosa = (b * b + c * c - a * a) / (2 * b * c);
    angle_c = Math.acos(cosc);
    angle_a = Math.acos(cosa);
    angle_b = 180 - angle_c - angle_a;
    return (angle_c <= 120) && (angle_b <= 120) && (angle_a <= 120);
}

接下来撒点就是水到渠成的事了：

var total = 0;  // 所有点数
var valid = 0;  // 符合条件的点

for (let x = 1e-7; x <= 0.99999; x += 1e-4) {
    for (let y = 1e-7; y <= 0.99999; y += 1e-4) {
        total ++;
        if ( check(x, y, 0, 0, 0, 1) &&
            check(x, y, 0, 1, 1, 1) &&
            check(x, y, 1, 1, 1, 0) &&
            check(x, y, 1, 0, 0, 0)         
        ) {
            valid ++;
        }
    }
}

console.log(valid);
console.log(total);
console.log(Math.round(valid / total * 1000) / 1000);  // 保留三位精度

增量试着从 1e-3 到 1e-6，因为小数点需要3位，所以 1e-3 之后精度就没有再变化了（天啊撸，我提交答案的时候以为需要的三位数是（乘以100后的） 21.255% 所以花了不少时间做了无用工，而且提交上去答案还算是错的了）

以上方法，不管你跑多少次，输出的结果一定是一样的，计算机学上我们称这种算法为 确定型 (Deterministic)

这种方法的复杂度是 O(xy)，当步长很小的时候需要的时候很不环保，我们可以试着用蒙特卡罗防真的方法：当我们随机往正方形内撒点的时候，撒足够多的点，那么符合条件的点除于总点数就是答案要的概率。

撸起袖子就是干：

const N = 10000000;

for (let i = 0; i < N; ++ i) {
    let x = Math.random(1.0);  返回【0，1） 闭包
    let y = Math.random(1.0);
    if ( check(x, y, 0, 0, 0, 1) &&
        check(x, y, 0, 1, 1, 1) &&
        check(x, y, 1, 1, 1, 0) &&
        check(x, y, 1, 0, 0, 0)         
    ) {
        valid ++;
    }
}

console.log(valid);
console.log(N);
console.log(Math.round(valid / N * 1000) / 1000);

注意：Math.random(1.0) 返回【0，1）闭包区间的随机值，我们不是说过不能等于0嘛，不能在正方形边上，不过没关系，这个误差可以忽略不计，因为本身这个模型就是随机采样的，本身就有少量误差！

跑几次的结果虽然都是 0.213 但是前面有效的点数会有小范围浮动，比如：

2126142
2127333
2125929
....

如果你的N少写几个零，那么精度就很有可能不够了，可能会输出 0.212, 0.214 这样很接近的值。这种方案的时间复杂度是 O(N) ，N也就是你的采样点数，可以根据需求调整，比如我只想大概知道概率，不需要很精确，那么我的N可以是1e4，这样也大概给出了 0.200， 0.215， 0.216， 0.204 这样的概率 （20%左右），而实现起来相当的快，运行速度也是秒出结果。有它的优势。

当然，如果你硬是说获取精度若是太高则需要的N很大，速度很慢，你是对的，但我们可以用并行计算来完成，比如 C++里，我们可以这么写：

int main() {
    srand(time(NULL)); // seed
    const int N1 = 1000;
    const int N2 = 100000;
    int n = 0;
    int c = 0;
    Concurrency::critical_section cs;
    Concurrency::parallel_for(0, N1, [&](int i) { // 并行 
        int t = check(N2);  //  并行小块分别统计
        cs.lock(); // 避免同时更新这个变量
        n += N2;   // 总样本
        c += t;    // 有效值
        cs.unlock();
    });
    cout < < "概率 ~= " << setprecision(9) << (double)c / n  << endl;
    return 0;
}

不止C++，其它语言 如C#里也有 Parallel For, 思路都是一样的，这里就不具体说了，可以看我之前写的相关C++博文（英文）: C++ Coding Exercise – Parallel For – Monte Carlo PI Calculation

---

@justyy 是CN 区的点赞机器人，对优质内容进行点赞，只要代理给 @justyy 每天收利息(100 SP 每天0.04 SBD)并且能获得一次相应至少2倍的点赞，可以认为是VP 200%+ ，详细请看：

• cn区最低保障系统 上线了!
• 虽然不挣钱，但是CN区低保计划还会继续下去

---

• Monte Carlo solution for Mathematics × Programming Competition #7
• 数学 × 程式编写比赛 (第七回) 蒙特卡罗撒点

欢迎你发表你的见解和看法，特别有意思的评论我可能会奖励你1 SBD哦。
Interesting Comments might be rewarded with 1 SBD.