Aplicación de modelos matemáticos en el campo de la física usando como herramienta ecuaciones diferenciales
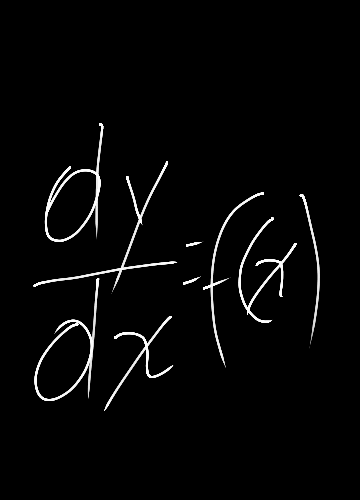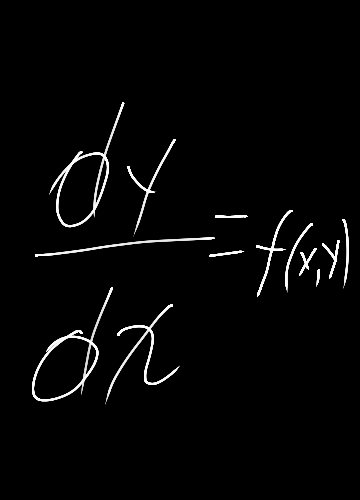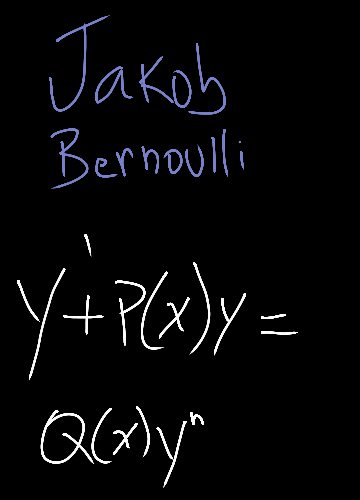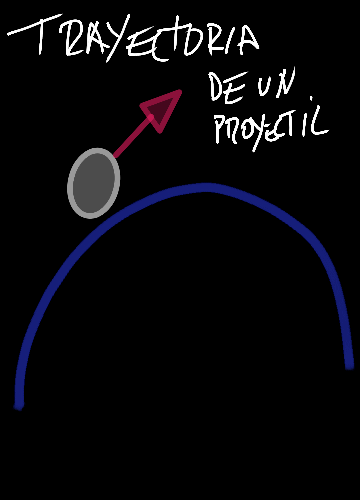
Con la información aportada por medio del vídeo introductorio tenemos entonces, que una ecuación diferencial es una ecuación matemática que relaciona una función con sus derivadas, el cual son de utilidad en la modelización y resolución de problemas que plantea dicha disciplina científica como en este caso en el campo de la física.
Puesto que la derivada dxldt= f`(t) de la función f es la razón a la cual la cantidad x = f(t)está cambiando con respecto a la variable independiente t, es natural que las ecuaciones que incluyan derivadas se usen con frecuencia, para describir el universo cambiante. Una ecuación que relaciona una función desconocida y una o más de sus derivadas se llama ecuaciones diferencial.Información consultada en Ecuaciones diferenciales por C. Henry Edwards, David E. Penney – 2000.

Una representación donde incluyen tanto a la función desconocida x(t), como a su primer derivada x´(t) = dx/dt, es importante también mencionar que lo primordial de la ecuaciones diferenciales, es esta va depender de la solución que se encuentre, con el fin de descubrir la ecuación diferencial en forma en que está descrita y aparte también, para determinar la solución bien sea exacta o aproximada de dicha ecuación en estudio.
Ya entrando en materia del campo de la física hay que tener las siguientes consideraciones, debido a que en parte del conocimiento científico se basa en estudiar los fenómenos físicos de manera muy general , con el fin después estudiarla de manera individual, ya que existen leyes que se manejan una series de magnitudes y unidades, lo que describen o caracterizan a los fenómenos en estudio, es por ello que se trata de aplicar la herramienta de modelo matemático que vincule las magnitudes o unidades y sus respectivas derivadas.
La segunda ley de Newton para una partícula de masa constante m, que se mueve en una dimensión espacial bajo la acción de una fuerza F. Si x denota la posición de la partícula y la fuerza F depende del tiempo t, de la posición x y de la velocidad v= dx/dt de la partícula, la ley F= ma, con a = d^2x/dt^2 la aceleración de la partícula.Información consultada en Ecuaciones diferenciales en física por Carlos María Naón, Raúl Dante Rossignoli, Eve Mariel Santangelo, 2014.

En el video introductorio mencionó el ejemplo cuando se la lanza un proyectil, donde este tiene una trayectoria cuya forma geométrica la cual esta origina es una curva, para definir este tipo de fenómeno es conveniente usar una ecuación diferencial ordinaria, de tal manera esta se obtiene a partir de la segunda ley de Newton. Adicional a esto es conveniente conocer, si en la ecuación diferencial la incógnita esta descrita por una función de una sola variable o que contiene una función de una variable independiente, adicional a esto esta se puede considerar lineal siempre y cuando su solución sea inmediata, donde dicha solución se pueden cumplir a sumarse y ser multiplicadas por coeficientes, lo cual está definida por la propia ecuación.
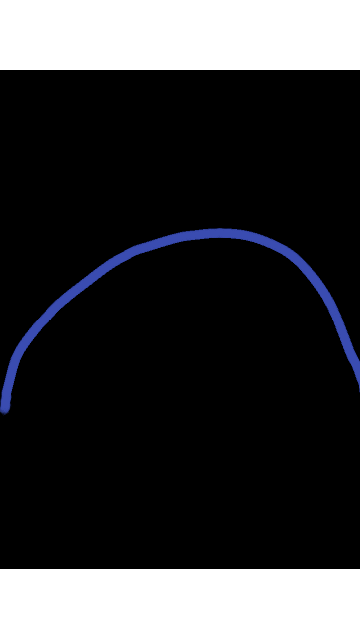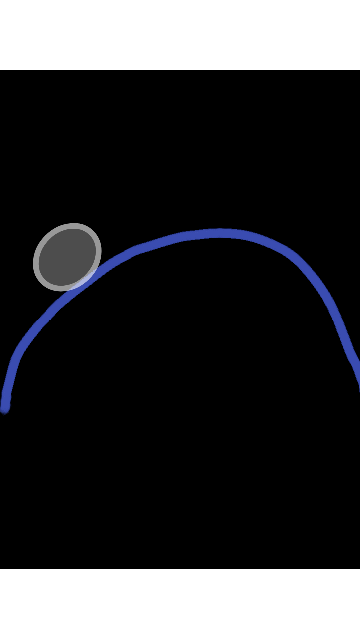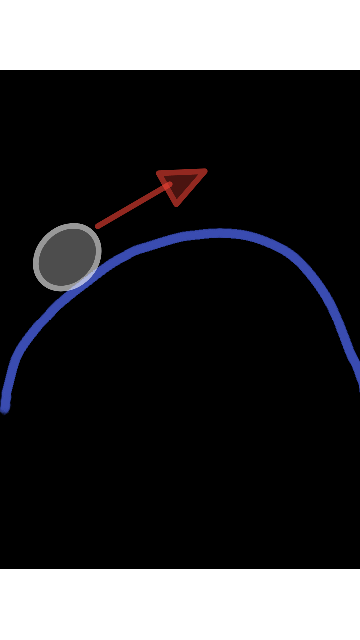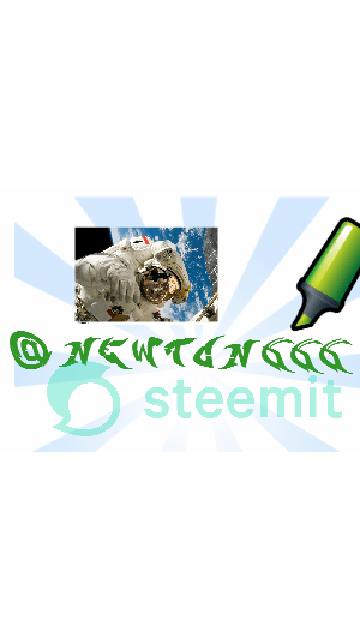
Una representación de la una curva definida por una ecuación diferencial ordinaria, que se obtiene a partir de la segunda ley de Newton, a partir de una trayectoria ejercida por un cuerpo o proyectil lanzado. En el campo de la física se evidencia el estudio de sistemas con número finito de grados de libertad, de tal manera propia para las ecuaciones de orden ordinaria.
Ecuación diferencial lineal de orden n: Una ecuación diferencial en ordinaria lineal de orden n, es una ecuación en la que la derivada n –sima de la variable y es una función lineal de las demás derivadas y de la propia función y, es decir de la forma:Información consultada en Ecuaciones diferenciales. Teoría y problemas por Ignacio Acero – 2007.
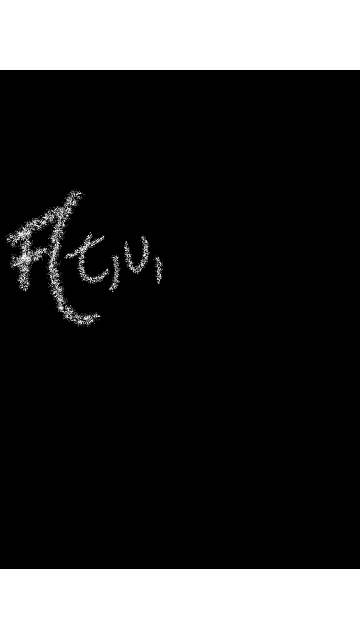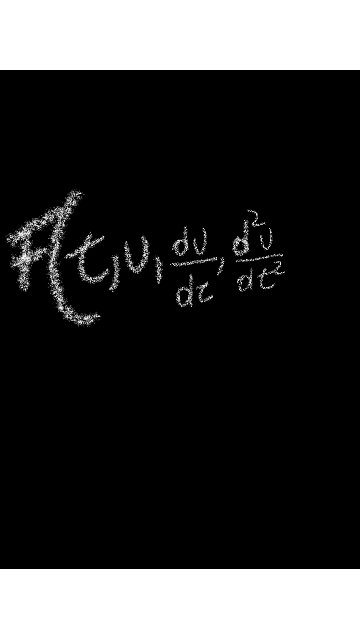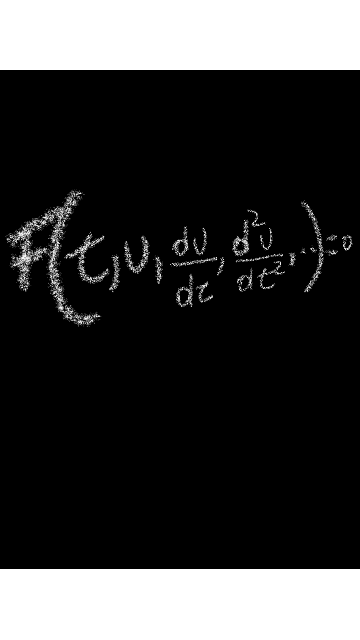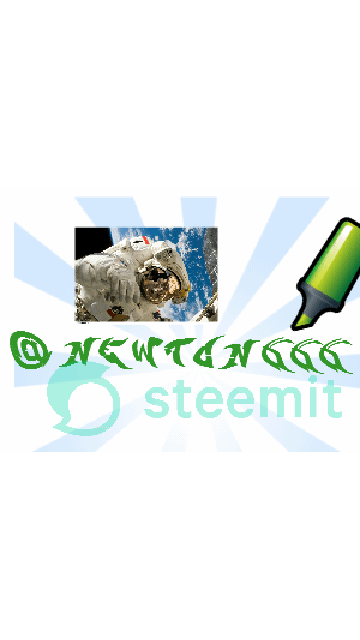
Parece mentira pero la realidad en el campo de física, se apoya mucho usando como herramienta de las ecuaciones diferenciales en el caso más de la lineares, saben compañeros lectores el porqué, por la manera de manejar las variables y sus incógnita en materia de la mecánica, circuitos cerrado, cambio s de temperatura bajo el esquema bidimensional.
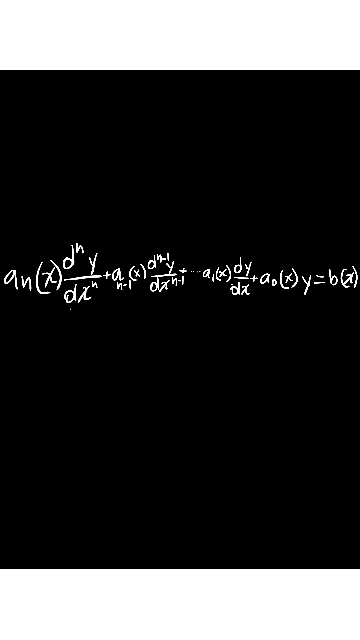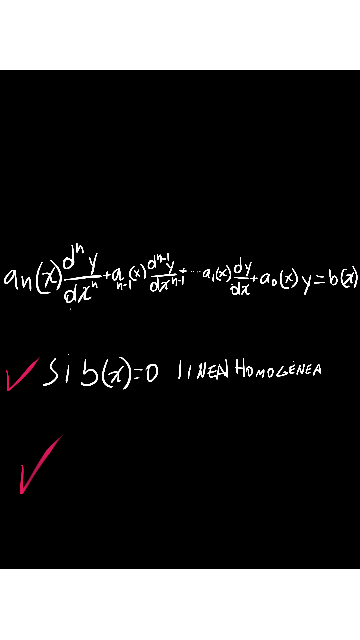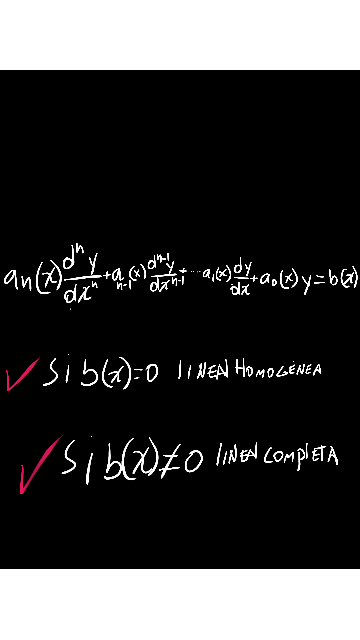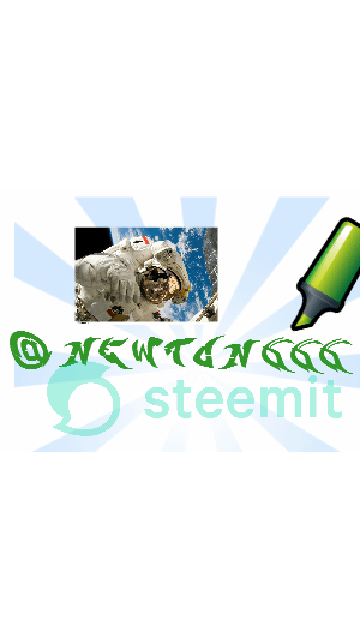
Ahora tenemos el siguiente caso donde tiene que ver oscilador armónico, dentro del campo de la energía cinética, ya que dentro de este sistema donde se puede evidenciar un fenómeno en libertad fuera de su posición de equilibrio, vuelve hacia ella describiendo oscilaciones sinusoidales hasta llegar la posición estable, dicho fenómeno físico nos muestra como toda la energía cinética se transforma en una energía potencial por medio de la oscilación, donde está alcanzaría con la misma amplitud, el cual se caracteriza por su frecuencia mediante su período, qué es el tiempo necesario para un ciclo completo del movimiento, es por ello que una oscilación libre es que la amplitud se mantiene constante y dicha energía total se mantiene constante también.

Una representación de la ecuación diferencial en el medio de oscilación, también considerando la segunda ley de Newton, bajo el esquema de movimiento armónico simple donde (y), es la distancia entre la posición de equilibrio y la masa (m), ya que la que la fuerza del resorte es estrictamente proporcional al desequilibrio: F = − k y, bajo el concepto de la ley de Hooke, de tal manera que (F), es la fuerza y (k ) la constante elástica del resorte, considerando también en cuanto la el signo negativo, nos indicara cuando (y), es positiva la fuerza está dirigida hacia las (y ), ahora bien en referencia de la ley de Hooke compañeros lectores, esta modeliza para casos de fenómenos físico que tiene la singularidad de estiramiento longitudinal, donde se evidencia que el alargamiento unitario el cual experimenta un material o cuerpo elástico, este es directamente proporcional a la fuerza aplicada sobre el mismo, en referencia del fenómeno de movimiento ejercido en él.


[1]-Ecuaciones diferenciales por C. Henry Edwards, David E. Penney – 2000.
[2]-Teoría y problemas por Ignacio Acero – 2007.
[3]-Ecuaciones diferenciales en física por Carlos María Naón, Raúl Dante Rossignoli, Eve Mariel Santangelo, 2014.

Muy educativo tu artículo @newton666, para los físicos en la edad antigua era muy importante establecer estas ecuaciones diferenciales, ya que muchos fenómenos de la naturaleza tienen un proceso cambiante en donde la derivada juega un papel primordial para darle solución al curso normal de estos fenómenos.
Tal es el caso de la velocidad instantánea, la cual se consigue con la primera derivada, la derivada de la posición con respecto al tiempo me da la velocidad, pero si derivamos la velocidad en un punto específico con respecto al tiempo encontramos la aceleración.
En unos de mis post tambien trate la importancia de las ecuaciones diferenciales en la interacción de las poblaciones, por lo que para mi resulta muy motivante leer artículos de esta índole, felicidades y gracias por contribuir con tan buen material.
Saludos @carlos84 gracias por compartir tus conocimiento esa es la dimanica de manejar este tipo de contenido, ya que los modelos matematicos han sido una herramienta muy fundamental en nuestra vida cotidiana
¡Felicitaciones!
Estás participando para optar a la mención especial que se efectuará el domingo 8 de septiembre del 2019 a las 8:00 pm (hora de Venezuela), gracias a la cual el autor del artículo seleccionado recibirá la cantidad de 1 STEEM transferida a su cuenta.
¡También has recibido 1 ENTROKEN! El token del PROYECTO ENTROPÍA impulsado por la plataforma Steem-Engine.
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Contáctanos en Discord.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Gracias @entropia por su apoyo y de valor mi post
Cool blog on math
Gracias por su valioso apoyo @ramonycajal y la comunidad de cervantes
Saludos! El vídeo está privado y no se puede visualizar!
buenas noches saludos @alexaivytorre ya puedes disfrutar del video introductorio de este post, ya se resolvió el inconveniente
Los temas de curvas en Steem han sido mencionado mucho estos días!
Saludos y gracias por su valioso apoyo @team-mexico
Saludos! buen material académico-audiovisual. Te invito a colocar el nombre del programa donde fueron realizados los gifs animados.
Gracias por el apoyo y la sugerencia @alexa.ciencia
Curamos la etiqueta #spanish con el token SPACO de la Comunidad de Hispano Hablantes, te invitamos a formar parte de nuestra comunidad.
Es un valioso saber de tener su apoyo @sinergica
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having added @steemstem as a beneficiary to your post. This granted you a stronger support from SteemSTEM.
Thanks for having used the steemstem.io app. You got a stronger support!
Gracias @steemstem por su valiosos apoyo y de valorar mi post
¿Al diferencial también se lo puede llamar Delta (delta y (dy), delta x (dx))?
Es una pequeña duda.