Reología del fluido de perforación. II parte
En esta segunda parte dedicada a la reología del fluido de perforación, quiero dar continuidad al flujo laminar, esta vez explicando los aspectos más relevantes del modelo de flujo plástico de Bingham. Teniendo en cuenta que los fluidos de flujo laminar tienen una diversidad en sus modelos, resulta necesario ir realizando una descripción a detalle de los mismos, en el post anterior estudiamos el modelo Newtoniano, del cual podemos resaltar que tiene un comportamiento lineal si lo analizamos en un gráfico de esfuerzo cortante versus tasa de deformación, y que si calculamos la pendiente de esta recta, estaríamos calculando la viscosidad del fluido.
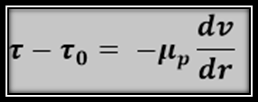






Introducción
Los fluidos que tenían un tipo de comportamiento en particular, al principio los reconoció fue Bingham, fueron llamados fluidos plásticos, para posteriormente ser llamados fluidos plásticos de Bingham. Cuando estudiamos el comportamiento que sigue un fluido bajo los estándares de este modelo, el modelo plástico de Bingham se diferencia notablemente de los fluidos Newtonianos, la diferencia es marcada en el hecho de que los fluidos cuyo comportamiento sea el modelo plástico de Bingham, necesitan un esfuerzo finito para poder iniciar su flujo.
En base a las conjeturas que se puedan hacer del modelo plástico de Bingham, en base a lo que es su comportamiento, modelos matemáticos, análisis de flujo, resulta necesario realizar una descripción en base a las ecuaciones que rigen su comportamiento junto con las gráficas que soporten estos comportamientos. Todos estos puntos serán abordados en el presente artículo, sin dejar de lado las aplicaciones e implicaciones que este modelo pueda tener con el transporte de fluidos empleados en la industria petrolera.
Ecuaciones que modelan el comportamiento del modelo plástico de Bingham
Si tomamos en cuenta que el modelo plástico de Bingham requiere un mínimo esfuerzo para iniciar su movimiento, y que existe una viscosidad plástica definida como el esfuerzo cortante en exceso, podemos definir la siguiente ecuación:
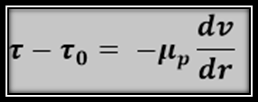
Esta ecuación modela el comportamiento de flujo plástico de Bingham, del cual el término tao sub cero representa el esfuerzo mínimo requerido para poder iniciar el flujo, y μ_p es la viscosidad plástica, si despejamos μ_p de la ecuación Nº1 obtenemos la siguiente ecuación:

Como el modelo que se está analizando es el plástico de Bingham, la resistencia que tenga cualquier fluido a poder fluir y que esté fluyendo bajo este modelo será una resistencia plástica, es decir una viscosidad plástica. La resistencia total a la deformación de un fluido plástico de Bingham, se puede expresar en términos de la viscosidad efectiva a una tasa de corte especificada.
Antes de poder expresar la resistencia total a la deformación en términos de la viscosidad efectiva, resulta necesario entender lo que es la viscosidad efectiva. La viscosidad efectiva se puede conceptualizar como la viscosidad que tiene un fluido newtoniano pero exhibiendo el mismo esfuerzo cortante a la misma tasa de corte, por lo que definir la resistencia total a la deformación en términos de la viscosidad efectiva se puede modelar con la siguiente ecuación:

Con esta ecuación podemos deducir que, la viscosidad efectiva se puede considerar como un tipo de viscosidad comprendida por dos factores: la viscosidad plástica, la cual corresponde a la viscosidad de un fluido newtoniano, y la otra es la viscosidad estructural, la cual representa la resistencia al corte del fluido, originada por la tendencia de las partículas a construir una estructura.
Análisis e interpretación del gráfico de la disminución de la viscosidad efectiva con incremento en la tasa de deformación

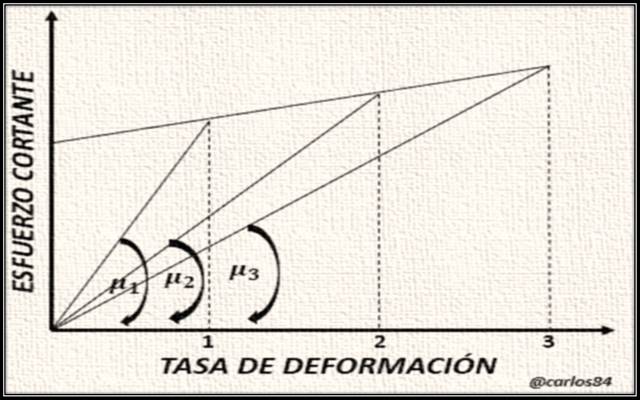
En el gráfico Nº1 tenemos varias viscosidades efectivas, a diferentes tasas de deformación: en la primera tasa de deformación podemos ver una viscosidad efectiva mayor, ya que el ángulo de inclinación de la primera recta es mayor. La segunda recta disminuye su ángulo respecto a la tasa de deformación, por lo que la viscosidad a la segunda tasa de deformación disminuye en comparación a la primera viscosidad. En la tercera tasa de deformación podemos observar que con un pequeño aumento del esfuerzo cortante obtenemos una tasa de deformación mayor, por ende una viscosidad del fluido menor que el expresado por la tasa de deformación 1 y 2.
En la figura también se observa que el cociente entre un esfuerzo inicial (tao sub cero) y la tasa de formación (gamma), va formando una proporción decreciente de lo que es una tasa de resistencia total al corte, todo esto ocurre a medida que la tasa de corte aumenta, de modo que la viscosidad efectiva va disminuyendo conforme aumenta la tasa de corte o deformación.
Todo esto se traduce en la vida real, en que a medida que aplicamos una mayor fuerza para que un fluido que ofrece resistencia se pueda mover, la resistencia a moverse de ese fluido disminuye, en la perforación de pozos el fluido de perforación ofrece una resistencia a desplazarse producto de los aditivos químicos que se le incorporan para que puedan mantener los recortes de la mecha en suspensión, pero a medida que la presión de la bomba de lodo aumenta, esta resistencia disminuye, y cuando se paga la bomba esa capacidad gelatinosa del fluido se activa nuevamente para mantener los recortes en suspensión.
Las bondades de entender este comportamiento del modelo plástico de Bingham es que un fluido que siga este comportamiento va disminuyendo su viscosidad efectiva a medida que es sometido a esfuerzos mayores.
Debo acotar que el valor de la viscosidad efectiva no llega a tener ningún significado salvo que se especifique la tasa de corte a la cual fue medida. La viscosidad efectiva no es un parámetro exacto para que se pueda comparar las propiedades viscosas de dos fluidos, si eso es lo que se quisiera, se requiere que por lo menos dos parámetros, sin embargo, la viscosidad efectiva es un parámetro muy útil cuando se utilizan ecuaciones hidráulicas en las que se conozca la tasa de corte.
El comportamiento de flujo plástico que se puede observar en el gráfico de la figura Nº1, es muy raro verlo en la práctica exacto con todas esas características que se ilustra en el gráfico, lo que puede pasar en la realidad con un fluido que siga el comportamiento plástico de Bingham tal y como lo indica la figura, es que el fluido cuando se encuentre a presiones por debajo del punto de cedencia, se puede llegar a observar un deslizamiento lento.
En el modelo plástico de Bingham se propone la existencia de un punto de cedencia del fluido, sin embargo Green logró demostrar que en este tipo de flujo, no estaba envuelta ninguna acción cortante, la suspensión fluía como un tapón sólido lubricado por un película delgada de líquido en las paredes del capilar, las partículas se mantienen juntas por las fuerzas atractivas entre ellas, por lo que Green concluyó que no existía punto cedente absoluto, por lo que tuvo que redefinir el concepto de punto cedente de Bingham de la siguiente manera: “es el esfuerzo cortante requerido para iniciar flujo laminar en la suspensión”.
Con lo mencionado anteriormente, Green demostró que el flujo plástico de Bingham en una tubería tiene el siguiente comportamiento: “si la presión es gradualmente aumentada desde cero, la suspensión al principio fluye como un tapón, y el perfil de velocidad es como una línea recta normal al eje central de la tubería tal y como lo muestra el gráfico de la disminución de la viscosidad efectiva con incremento en la tasa de deformación”.
Análisis de la ecuación del flujo laminar en las paredes de una tubería
Ya que, el esfuerzo cortante es igual a rP/2L el flujo laminar comienza en las paredes de la tubería cuando el fluido modela su flujo bajo la siguiente ecuación:

Donde Po es la presión requerida para iniciar el flujo del fluido plástico a presiones mayores Po, el flujo laminar progresa hacia el eje central de la tubería, de forma tal, que el flujo consiste de un tapón en el centro de la tubería, de tal forma que el flujo consiste de un tapón en el centro de la tubería rodeado por una zona de flujo laminar, y el perfil de velocidad es como el mostrado en el gráfico de la figura Nº1.
Sin importar cuán grande sea la presión, este tapón nunca puede ser enteramente eliminado, debido a que a medida que r se vuelve muy pequeño, P se tiende a volver muy grande, e infinito cuando r= O, así que la curva de consistencia para el flujo de un fluido plástico de Bingham en una tubería es, estrictamente no lineal, sin importar cuán grande sea la tasa de corte.
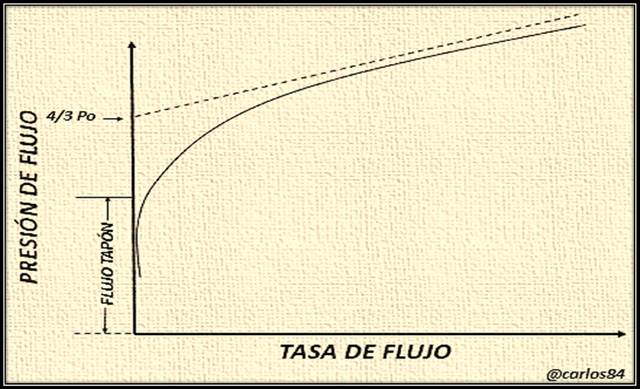
Análisis del gráfico presión de flujo versus tasa de flujo

Este gráfico expresa una curva de consistencia, la cual se observa en un fluido que siga el comportamiento plástico de Bingham, donde Po es el punto cedente real, mientras que 4/3 Po es el punto cedente aparente.
También es importante resaltar que existe una relación aproximada entre presión y tasa de flujo, los cuales se derivan de la asíntota de la curva mostrada en el gráfico. En este gráfico se representan una serie de variables que no están explícitas en sí, pero que si se correlacionan con un modelo de ecuaciones deben de involucrar variables como el área existente entre la curva total y la asíntota.
Utilidad de emplear el viscosímetro rotatorio cilíndrico concéntrico
La viscosidad plástica es el tipo de viscosidad que presentan los fluidos que siguen el comportamiento de flujo del modelo plástico de Bingham, y que junto al punto cedente son dos propiedades de suma importancia al momento de estudiar y analizar el transporte de fluidos. Es por ello que resulta conveniente obtener las lecturas de estas dos propiedades con el viscosímetro cilíndrico rotatorio concéntrico. La principal ventaja de este instrumento es que a una cierta velocidad del rotor, se elimina el flujo tapón, haciendo que la curva de consistencia se transforme en lineal.
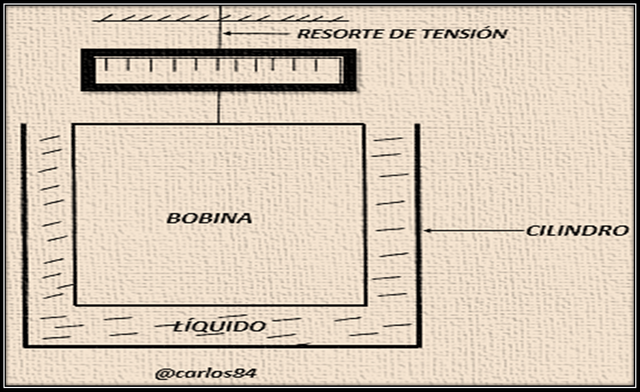
Dentro de los elementos esenciales del viscosímetro, tenemos un cilindro exterior que gira concéntricamente alrededor de un cilindro interior o bobina, la cual está suspendida de un resorte de torsión.
El espacio anular entre la bobina y el cilindro exterior es angosto, alrededor de 1 milímetro aproximadamente. Una escala fijada al soporte de torsión y un indicador fijo, lo capacita para medir el ángulo de torsión del resorte cuando da vuelta.
Cuando el cilindro exterior rota, la bobina rota con él, ocurriendo un deslizamiento menor, hasta que el torque en el resorte crea un esfuerzo cortante en la superficie de la bobina, mayor que la resistencia cortante de la estructura plástica, es en ese momento donde podemos aplicar la siguiente ecuación:

En donde To es el torque que se obtiene a la lectura del punto cedente, Rb es el radio de la bobina, y h es la altura efectiva de la bobina, es decir, la altura real de la bobina más una corrección para el efecto de extremo del fondo de la bobina. El flujo laminar, ahora comienza en la superficie de la bobina y progresa hacia afuera con la continuación de la rotación hasta que todo el fluido en el anular está en el flujo laminar. A continuación se muestra la figura donde se detallan las partes de un viscosímetro de torsión:

Aporte de esta publicación a la ingeniería y perforación de pozos
El estudio y rango de viscosidades es muy importante en el transporte del fluido de perforación, ya que los valores de viscosidad deben tener un equilibrio donde no sean tan alta como para que necesiten altos valores de presión de bomba, pero a su vez que sea lo suficientemente alta para lograr mantener los recortes en suspensión cuando la circulación de lodo se pare.
Como está claro, que los valores y lectura de las viscosidades del fluido de perforación son de suma importancia, entonces la técnica empleada para medir la viscosidad depende del viscosímetro y la toma de las lecturas.
Por ejemplo en la evaluación de los lodos de perforación, es muy común para los ingenieros de lodo de perforación reportar la viscosidad efectiva a una lectura de 600 revoluciones por minuto (RPM). Esta cantidad es la llamada viscosidad aparente (VA) y está dada por la siguiente ecuación:

Es importante mencionar que la viscosidad aparente se puede obtener con la lectura del viscosímetro rotacional con solamente la lectura a 300 RPM, en caso tal de que se tenga a mano la lectura de 600 RPM, es necesario que ese valor que se tenga de viscosidad con la lectura de 600 RPM se divida entre dos.
En la industria petrolera, y en especial en perforación de pozos, el término viscosidad aparente es usado para que en un sentido más general exista una alternativa para el término viscosidad efectiva.
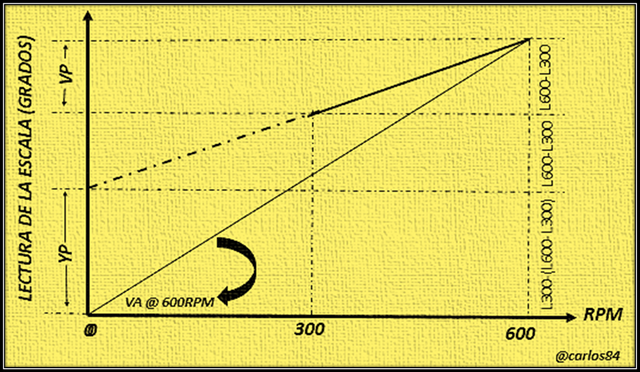
La base para la determinación de la viscosidad plástica, punto cedente y viscosidad aparente, se muestra continuación el siguiente gráfico:

La importancia de la interpretación de este gráfico está en que si calculamos las pendientes de las rectas, podemos obtener los cálculos de tres tipos de viscosidades distintas, las cuales cumplen con funciones específicas en el fluido de perforación, estas viscosidades son:
[1] Viscosidad aparente: esta viscosidad, como se puede observar en el gráfico se obtiene de la lectura a 600 RPM/2 del viscosímetro rotacional.
[2] Viscosidad plástica: Lectura a 600 RPM – Lectura a 300 RPM
[3] Punto cedente (YP): Lectura a 300 RPM – Viscosidad plástica = L300 – (L600 – L300).
Cualquier interpretación o análisis realizado en base al gráfico de determinación de parámetros de flujo como viscosidad aparente, viscosidad plástica y punto cedente (YP) en un viscosímetro rotacional, es necesario que este viscosímetro tenga un indicador de dos velocidades, una velocidad a 300 RPM y a 600 RPM.
En conclusión, con el aporte de este artículo podemos establecer la base para poder comprender las deducciones de las ecuaciones que rigen el comportamiento de un fluido plástico, a medidas que avancemos en el estudio de la reología e hidráulica del fluido de perforación es necesario que se tengan consolidados los modelos de flujo de fluidos como newtonianos, plástico de Bingham y ley de potencia.
Nota: La elaboración de las imágenes y ecuaciones son de @carlos84 empleando las herramientas de Microsoft PowerPoint.
Referencia consultada
Perforación de pozos. Programa de postgrado en Ingeniería de Petróleo. Centro de Formación y Adiestramiento de Petróleos de Venezuela y sus filiales.Referencias recomendadas
[1] ESTUDIO DE UN LODO DE PERFORACIÓN DENSIFICADO por @ennyta en steemit.[https://steemit.com/stem-espanol/@ennyta/estudio-de-un-lodo-de-perforacion-densificado]
[2] Viscosidad del lodo de perforación por scribd.[https://es.scribd.com/document/287012689/Viscosidad-Del-Lodo-de-Perforacion]
[3] Punto cedente por perfoblogger.[http://perfob.blogspot.com/2015/07/que-es-el-punto-cedente.html]
_____________________________________________________
"Para toda aquella persona que le apasiona la matemática, física, química, biología, educación e ingeniería, le recomiendo la etiqueta de #stem-espanol, es una comunidad que valora el contenido intelectual y académico de calidad, conservando siempre la originalidad de las publicaciones, por lo que se recomienda a todos aquellos amigos de steemit que deseen publicar utilizando esta etiqueta a no cometer plagio."

¡Felicitaciones!
Estás participando para optar a la mención especial que se efectuará el domingo 14 de julio del 2019 a las 8:00 pm (hora de Venezuela), gracias a la cual el autor del artículo seleccionado recibirá la cantidad de 1 STEEM transferida a su cuenta.
¡También has recibido 1 ENTROKEN! El token del PROYECTO ENTROPÍA impulsado por la plataforma Steem-Engine.
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Contáctanos en Discord.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @utopian-io.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness and utopian-io witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having added @steemstem as a beneficiary to your post. This granted you a stronger support from SteemSTEM.
Thanks for having used the steemstem.io app. You got a stronger support!
Hi @carlos84!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV