Crystal structures: understanding the strength of materials from "first principle"
Matter can be defined in straight terms as anything that has inertia and occupies space (not space, as in astronomical space, lol). It exists in four basic form; the liquid, solid, gas and plasma. The major focus of this work is on the incompressible state of matter, the solid. Ever wondered why two different solids have different strengths? ever wondered why solid with the same chemical makeup would have different physical strengths and possibly appearance? Well, we're here to find out and more.
Image source Publicdomainpictures. CC0 public domain license.
The first time I heard about crystals (or better still saw crystals) I was around the age of 8. I always hate carrying out instructions just the way they were given to me and on this very day, my mother told me never to leave the house for any reason and of course she knew I would disobey. I came back later in the day to discover she came home before me, I received the dirtiest slap of my life that day and as I was trying to process the stars in my head, I heard her yelling at me "I hope I've made myself crystal clear", that was when I knew the stars in my head actually was crystals and I never forget the word, lol.
Solids are made up of atoms and these atoms have electrons revolving around them in a definite path known as orbit, different layers of these orbits are known as shell(s). Just as there're varieties of atoms, there are also different amount of electrons that can be accommodated in the respective shell of these atoms. While some atoms have their shells filled with electrons, some atoms have their shells half or partially filled with electrons and this in turn account for their physical characteristics, hence, solids are broadly classified as either crystalline solids or amorphous solids.
Any solid in which its atoms are arranged orderly is regarded as crystals, conversely, any solid that has its atoms arranged randomly is regarded as amorphous solid.
Unit cell and the lattice
No doubt, diamond is the hardest solid known to man but what if I tell thee that it has something in common with the salt we take everyday? Well, look no further, they both are made up crystals, the atoms making up these solids are arranged in an orderly manner maintaining the space between each other and repeating the same pattern to form a perfect three dimensional structure.
))
Lattice represents the orderly distribution of atom within solids. Image credit Wikimedia. CC0 Creative Commons license.
Lattice is a word used to describe these perfect arrangement of atoms in crystalline solids. In order to better study crystals, a point or a dot is used to represent a particular atomic distribution, this dot is known as the lattice point.
A collection of these points forms what is known as lattice site and these lattice sites are highly symmetrical. When I say that the lattice sites are symmetrical, it means that each of the sites are similar in all aspects which include the composition and arrangement of atoms within them. Let's zoom in on the concept of symmetry.
Symmetry in crystalline solids
As stated earlier, the atoms of crystalline solids are arranged in a definite an repetitive and spread out in a three dimensional manner and we refer to these different orderly arrangement as the crystal lattice. A careful examination of the surface of any crystal will reveal the internal structure of such crystal and this is because, in the absence of defects, the formation of a crystal starting from the atomic level repeats the same pattern up to its surface.
Consider a single square lattice site which of course is composed of perfect arrangement of atoms, when we place this imaginary lattice site in a perfect horizontal position and rotate it at an angle of 90o, 180o, 270o and 360o, we would notice that this crystal lattice will still look perfectly the same whether the rotation was done clockwise or in ant-clockwise direction. This is the manifestation of the concept of symmetry and crystals that exhibit such arrangement is said to have rotational 4 fold symmetry.
Illustration by @henrychidiebere
The characteristic symmetry described above depicts one out of three broad symmetries exhibited by crystalline solids at their surface (this is internally the same), the other two being inversion symmetry and reflection symmetry. Reflection symmetry which is also known as mirror symmetry and a crystal is said to exhibit a reflection symmetry if exposing half of the lattice plane to an imaginary mirror produces exact image of the other half.
The concept of symmetry is a very interesting one generally because every symmetrical operation posses no physical threat to the crystal as we can see in the example of 4 fold symmetry of a square lattice. But then, one might ask, of what importance is this since it have no physical effect on the crystal? Well, symmetrical operations help us to predict the molecular behaviors of crystals (including their interactions with light which is of high importance in producing imaging equipment), the possible movements of atoms making up the crystals, studying the atomic and molecular bonding of the crystals and so much more.
The Unit Cell
In our quest to further understand and simplify the underlying concept of crystals, we stumble upon the unit cell. As stated above, lattices or lattice points help us in the description of atomic distribution of crystals.
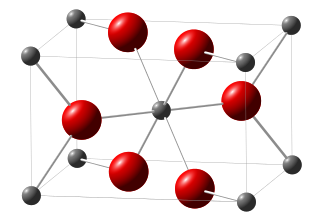))
A unit cell belonging to titanium dioxide. Image credit Wikimedia. CC0 creative commons license.
Also as stated earlier, just as there are many distributions of crystals, there are also many distributions of lattice structures and at some point, differentiating between these lattice structures became very difficult, hence, there was a need to come up with a generally accepted conventions for describing different lattice structures.
A unit cell can be in two dimensions and or in three dimensions. In three dimensions, it is a parallelopiped structure while in two dimensions, it is a parallelogram. In either of the shapes, their vertices represents lattice points. The symmetry of a unit cell represents the symmetry of the entire crystal, this shows how the concept of a unit cell simplifies crystallography. We can represent a complete crystal structure by repeating unit cells, in fact, different crystals are made up of different repeating unit cells.
Primitive Unit Cell
The unit cell is broadly classified as primitive and non-primitive cell. I would like us to consider a very popular geometrical shape, the cube. A cube clearly contains eight vertices (i.e, eight pointy sides), with the cube in mind I'll say that the simplest unit cell is the simple cubic cell. This type of unit cell is known as a primitive cell, let me explain why.
))
A tetragonal unit cell of the primitive type. Image credit Wikimedia. Creative Commons Attribution 3.0 Unported license.
As stated above, the vertices of these unit cells represents a lattice point but in real sense, the simple cubic with eight vertices has a single lattice point; someone might say that I've lost it but yeah, it contains just a single lattice point and here's why;
though the cube has eight vertices, each of the point on the vertex represents 1/8 of the lattice point and summing these lattice points give us a single lattice point this is because each of the lattice point "representation" is shared by other eight unit cells, remember, a unit cell is just one out of many.
Hence, a primitive cell is any cell whose summation of lattice points equals a one and is therefore the smallest obtainable cell.
The non-primitive unit cell
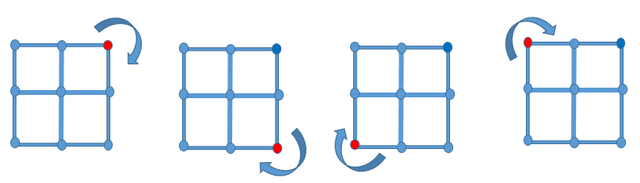
From the definition above, the concept of non-primitive cell is obvious; any cell whose summation of lattice points is greater than one. For a better understanding of the concept above, consider the diagram below,
))
Image designed by @henrychidiebere using MS word
we can observe four squares with different colors for better visuals, the points represent lattice points. At the center of these squares is a lattice point which is clearly being shared by these four squares, hence for this type of lattice structure, each point on the square represents 1/4 lattice point for that particular square and summing the points on the vertex would give a one (1/4*4).
Hence, the lattice structure represented by each of the unit cell is a primitive unit cell. Now, consider the parallelogram shown below with lattice points at the vertices colored in red for visibility. The sector of the lattice point covered by this particular parallelogram are labelled A to D. Clearly, A is equal to D and B is also equal to C. Applying simple geometry to the areas of the lattice points, we will realize that area A is equal to 1/3 of the whole lattice point while area B is equal to 1/6 of the whole lattice point.
))
Image designed by @henrychidiebere using MS word
Since A is equal to D and is also equal to 1/3, hence, A + D is equal to 1/32 which is equal to 2/3. Similarly, B is equal to C and is also equal to 1/6, hence, B+C is equal to 1/62 which is equal to 1/3.
Summation of the surface lattice for this parallelogram implies adding 1/3 and 2/3 which will be equal to 1. Did you observe the lattice point in the middle colored differently? Hence, the total lattice point for this type of lattice structure is 2. This type of lattice structure is known as body centered lattice structure.
Lattice system
Since we've understood the concept of lattice and unit cell, we can now discuss the lattice system. Lattice system simply mean the classification of lattices in accordance with the shape of their unit cell. A French physicist known as Auguste Bravais was popularly known for his work in the study of crystal especially in classifications of crystals. According to Bravais who put forward 14 different shapes of lattices called Bravais Lattices, these shapes are only possible in three dimensional space.
We have seven crystal systems which are cubic, monoclinic, triclinic, orthorhombic, trigonal, hexagonal and tetragonal crystal classes or families. The cubic crystal is characterized by equal length of sides and equal angle between each of these sides. It is the simplest of all cubic families. From the bravais perspective, the cubic crystals consists of face centered cubic and body centered cubic.
))
In accordance with appearance; Cubic P(1), Cubic I(2), Cubic F(3), Tetragonal P(4), Tetragonal I(5), Orthorhombic P(6), Orthorhombic C(7), Orthorhombic I(8), Orthorhombic F(9), Monoclinic P(10), Monoclinic C(11), Triclinic(12), Rhomboedral(13), Hexagonal(14). Image credit Wikimedia. Image by BruceBlaus. Creative Commons Attribution 3.0 Unported license.
The body centered cubic (because of the presence of a lattice point in its center) is very similar to the second illustration I gave under the non-primitive unit cell, the only difference is that for the cubic crystals, the angles and the sides are equal, hence the lattice point at any of the eight vertex is 1/8 and the summation of the eight vertices gives a unity plus the single lattice point in the center. Hence, the body centered cubic has 2 crystal points.
The face centered cubic crystal lattice structure unlike the body centered crystal has lattice points both at its vertices and also a single point at the center of each face. Since the lattice at the center is share by only two lattice structures, each of the point at the center is equal to 1/2 lattice point while each of the point at the vertex is shared by eight crystal lattice structure and is equal to 1/8. Since the cube has six sides, the total lattice point at the sides is equal to 1/2 6 while the total lattice point at the vertices is equal to 1/88 this gives a total lattice points of 4 for the face centered cubic
I'll stop at the cubic crystal system so this work won't be too lengthy but the concept is almost the same just that the rest of the lattice systems have varying angles between the sides of these shapes and varying angles between them.
Crystal Defects
The descriptions of crystal above was done with the assumption that many factors were kept constant but in reality, it is extremely difficult or impossible to grow a crystal that is 100% pure and free from defects, this is just like saying that there are no ideal gas in reality. In our discussion above, we described crystals as having a perfect arrangement of atoms but in reality, due to some, factors which could be intentionally introduced, crystals does not have perfect atomic distribution or perfect lattice structure.
))
Different forms of point defects. Image credit Wikimedia. Creative Commons Attribution 3.0 Unported license.
One of our own @rharphelle loves and talks about anything resting on a wheel and we know what 90% of today's wheels are made of; alloys. Alloys are produced by carefully and intentionally introducing impurities during the formation of crystals. Though imperfections naturally occur in crystals that were intended or targeted to be perfect. Silicon wafers used in creating computer chips are one of the crystals that are made with the target of 100% purity but they're never 100% pure crystals.
There are three basic crystal defects which include planar defects, point defects and linear defects. These terms are used to describe whether the defect is located in the whole volume of the crystal (planar defect), located at a restricted point or points (point defect) or located along a line or lines on the material in question. In the case of alloy stated above, imperfections were created intentionally in order to increase the strength of the material, hence, defects are not always bad for us.
Applications and summary
The study of crystals and their properties have led to tremendous development in the field of material sciences. The czochralski process which is a very popular method for growing high quality silicon crystals for making computer chips was developed through the study of crystals. Also metal alloying which has redefined today's motoring was developed through the knowledge and study of crystals.
From a scientific point of view, the study of crystals has resulted in over 27 Nobel prices which exceeds any other field and this shows its impact to humanity.
REFERENCES
- Crystal structure ~Wikipedia
- Unit cells ~chemed
- The symmetry of crystals ~xtal
- Crystal system ~wikipedia
- Bravais lattice ~wikipedia
- Crystal defects ~nde-ed
If you write STEM (Science, Technology, Engineering, and Mathematics) related posts, consider joining #steemSTEM on steemit chat or discord here. If you are from Nigeria, you may want to include the #stemng tag in your post. You can visit this blog by @stemng for more details. You can also check this blog post by @steemstem here and this guidelines here for help on how to be a member of @steemstem. Please also check this blog post from @steemstem on proper use of images devoid of copyright issues here.


This reminds me of my crystallography class many years ago. Thanks for sharing!
Thanks @irelandscape same here, this is my first material sciences post. I wanted to feel the good old days again
This reminds me of material science and engineering, one of the first topics we dealt with in the course. Lattices, BBC,FCC, the phase angles etc.
However, do you know that there are more states of matter? not just four
More than 4 states? Please help me with the remaining states. I though I mentioned them all.
The post wasn't exhaustive, I thought about talking about miller indices and all that but things were getting too long. As always, thanks @rharphelle
well, saying four states is actually fine but if you tell that to particle physicist, he would disagree.
you can check here to see the other states.
Crystals and solid molecule structure has been in our science books. You reminds me of my school days when science was my favorite subject. Nice post with lot of information.
Thank you so much man.
You are welcome dear!
Good post, congratulations. Are you physicist?
Not really, I'm more of network and computer technology person but as an advanced engineer, I have good knowledge of these fields
That is good. In physics, the structural properties are very important, principally in materials technology. Respects my friend.
Great part here everything to understand the atomic structure of each material, the physics of the solid state is fantastic.
thanks buddy
This reminds me of my undergraduate chem classes. This stuff was always fascinating, even though it never ended up being too useful after I moved into molecular biology. Thanks for the reminder!
Congratulations! Your post has been selected as a daily Steemit truffle! It is listed on rank 4 of all contributions awarded today. You can find the TOP DAILY TRUFFLE PICKS HERE.
I upvoted your contribution because to my mind your post is at least 23 SBD worth and should receive 163 votes. It's now up to the lovely Steemit community to make this come true.
I am
TrufflePig, an Artificial Intelligence Bot that helps minnows and content curators using Machine Learning. If you are curious how I select content, you can find an explanation here!Have a nice day and sincerely yours,

TrufflePigHi @henrychidiebere!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Congratulations @henrychidiebere! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard!
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes