Aplicación de las Ecuaciones Diferenciales Ordinarias en la Datación de Fósiles mediante el Isótopo Radiactivo Carbono-14 y su resolución mediante el Método de Runge-Kutta de 4° orden

Fuente: Kkorvin, Imagen de Dominio Público CC0. Disponible en Pixabay

Hola estimados lectores de Steemit y miembros de la comunidad científica #stem-espanol el día de hoy abordaré en mi artículo una de las aplicaciones de las Ecuaciones Diferenciales Ordinarias, específicamente la relacionada con la datación (determinación de la antigüedad) de fósiles mediante el uso del isótopo radiactivo del carbono-14, para lo cual en primer lugar se explicarán algunos conceptos previos.

El término vida media de un isótopo se usa para medir la estabilidad de una sustancia radiactiva, específicamente, la vida media es el tiempo que tardan la mitad de los átomos presentes en una cantidad de sustancia en desintegrarse. Si una sustancia tiene una vida media más larga que otra significa que su isótopo es más estable. Por ejemplo, el isótopo de Uranio que con mayor frecuencia se presenta en la naturaleza el U-238 tiene una vida media de aproximadamente 4.500 millones de años, esto quiere decir que en este periodo de tiempo la mitad de los átomos de Uranio U-238 se desintegran y producen como resultado otra sustancia (en este caso Plomo Pb-206).

La vida media de una sustancia radiactiva puede ser modelada mediante una ecuación diferencial ordinaria teniendo en cuenta que la razón a la que disminuye la cantidad de una sustancia radiactiva dA/dt es proporcional a la cantidad de sustancia radiactiva A, se establece el siguiente problema de valor inicial (P.V.I.):

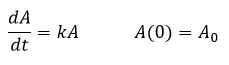
Donde A₀ es la cantidad original de la sustancia. Esta ecuación diferencial es muy fácil de resolver utilizando el método del factor integrante. El procedimiento para resolver una Ecuación Diferencial Ordinaria lineal de 1° orden es el siguiente, dada una E.D.O de la forma:

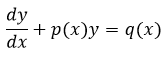
Se encuentra el factor integrante

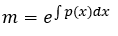
Luego la solución de la ecuación diferencial ordinaria lineal de 1° orden viene dada por la siguiente fórmula

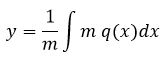
Aplicando estas fórmulas a la ecuación diferencial para la desintegración radiactiva se obtiene

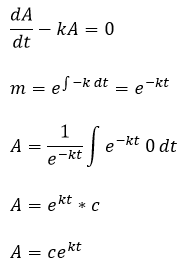
Sustituyendo la condición inicial se obtiene

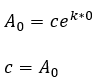
Es decir, la solución particular de la E.D.O. es

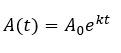
Esta ecuación diferencial ordinaria puede ser utilizar para el fechado por carbono-14, el fundamento de este método se basa en el hecho de que en la atmósfera terrestre ocurre una reacción química de gran relevancia tal como plantea Chang (2003)

“Una de las reacciones importantes entre la atmósfera y los rayos cósmicos es la captura de neutrones por el nitrógeno atmosférico (el isótopo nitrógeno-14) para producir el isótopo radiactivo carbono-14 e hidrógeno…”

La proporción entre el carbono-14 y el carbono ordinario de la atmósfera terrestre es constante y en general la proporción de carbono-14 presente en cualquier organismo vivo es similar a la de la atmósfera, sin embargo, cuando un organismo muere deja de absorber carbono-14, debido a esto al transcurrir los años la proporción de carbono-14 presente en el fósil del organismo tiende a disminuir este hecho es usado por los científicos para establecer la fecha en la que murió el organismo.

El método para fechar mediante el uso de carbono-14 fue desarrollado por Willard F. Libby en el año 1955 (este trabajo le hizo ganar el premio Nobel de química en el año 1960), para aplicar el método descrito se debe tener en cuenta que la vida media del isótopo carbono-14 es de aproximadamente 5.600 años.

Por ejemplo, si se encuentra un fósil que tiene un 1% de la cantidad original presente en la atmósfera de C-14, se puede determinar la edad de dicho fósil mediante la siguiente ecuación diferencial ordinaria

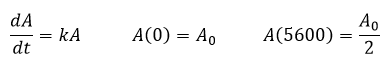
Se estableció la condición inicial

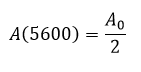
Debido a que en 5.600 años la cantidad de C-14 presente en el fósil se habrá reducido a la mitad. Teniendo en cuenta que, según se demostró al principio de este artículo la solución general de esta ecuación diferencial es

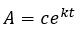
Sustituyendo la primera condición inicial

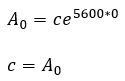
Es decir:

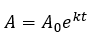
Sustituyendo la condición

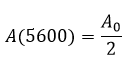
Se obtiene

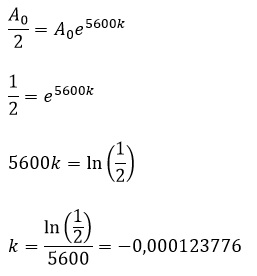
Es decir,

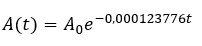
Como la proporción de carbono-14 es el 1% de la concentración original, reordenando se cumple que

Es decir, el fósil tiene una edad aproximada de 37.206 años.

Método de Runge-Kutta de 4° orden

Muchas veces los métodos analíticos utilizados para resolver Ecuaciones Diferenciales Ordinarias no son suficientes para encontrar una solución exacta, en estos casos se suelen aplicar métodos numéricos basados en aproximaciones, en un artículo anterior se abordó uno de estos métodos, el método de Euler el cual es la base de la mayoría de métodos numéricos utilizados para resolver Ecuaciones Diferenciales Ordinarias.

Uno de los métodos más utilizados para abordar este tipo de problemas de forma numérica es el denominado Método de Runge-Kutta de 4° orden (abreviado comúnmente como RK4), el cual pertenece a una conocida familia de métodos iterativos desarrollados en los años 1900 por los matemáticos alemanes Carl David Tolmé Runge y Martin Wilhelm Kutta.

El método de Runge-Kutta de 4° orden ha alcanzado gran popularidad debido a su gran precisión y a la simplicidad con la que es programado, adicionalmente el método solamente requiere una condición inicial, las fórmulas utilizadas en este método son las siguientes:

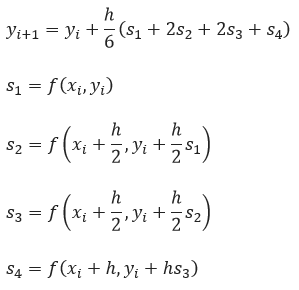
Básicamente se trata de estimar el valor de Y_i+1 mediante el valor anterior Y_i al cual se le suma el tamaño del intervalo h multiplicado por el promedio ponderado de la pendiente de f(x,y) en dicho intervalo permitiendo de esta forma obtener una aproximación bastante precisa a la solución de la ecuación diferencial ordinaria en el nuevo punto.

Este método puede ser aplicado al problema mostrado en el presente artículo, expresando la cantidad de carbono-14 de forma porcentual, se puede establecer que un organismo vivo al momento de morir posee una concentración de 100% la cantidad de C-14 presente en la atmósfera y utilizando el valor de k obtenido anteriormente

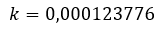
Se puede expresar la ecuación diferencial ordinaria como

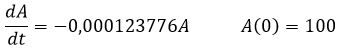
Se aplicará el método de Runge-Kutta para determinar cómo evoluciona la concentración de C-14 los primeros 200 años tras la muerte del organismo utilizando para ello el sistema de Álgebra Computacional (CAS) wxMaxima mediante el siguiente código fuente:


/******************************/
/* MÉTODO DE RUNGE-KUTTA /
/ Licdo Ysmael González /
/ STEM-ESPANOL /
/ STEEMIT 2018 /
/******************************/
f(x,y):=-0.000123776x$ /Ecuación diferencial a resolver/
x0:0$ y0:100$ /Condición inicial X0 y Y0/
xf:200$ deltax:5$ /Valor final del intervalo Xn y tamaño de paso/
sol(x):=100exp(-0.000123776x)$ /Solución analítica de la EDO/
fpprintprec:9$ /Número de cifras decimales/
xn:x0$ n:0$ yn:y0$ iter:(xf-x0)/deltax$
while n<=iter do
(
s1:float(f(xn,yn)),
s2:float(f(xn+(deltax/2),yn+(s1deltax/2))),
s3:float(f(xn+(deltax/2),yn+(s2deltax/2))),
s4:float(f(xn+deltax,yn+(s3deltax))),
g:float(sol(xn)),
ep:float(abs((g-yn)100/g)),
print("",n,"",float(xn),"",float(yn),"",float(g),"",float(ep),""),
n:n+1,xn:xn+deltax,yn:float(yn+(deltax/6)(s1+2s2+2*s3+s4))
);


Generando los siguientes resultados

Iter.	Año	% de C-14 (RK4)	Val. Exacto	Error %
0	0.0	100.0	100.0	0.0
1	5.0	99.9984528	99.9381311	0.060358997
2	10.0	99.9938112	99.8763006	0.11765617
3	15.0	99.9860752	99.8145082	0.17188578
4	20.0	99.9752448	99.7527542	0.22304211
5	25.0	99.96132	99.6910383	0.27111938
6	30.0	99.9443008	99.6293606	0.31611187
7	35.0	99.9241872	99.567721	0.35801379
8	40.0	99.9009792	99.5061196	0.39681939
9	45.0	99.8746768	99.4445563	0.4325229
10	50.0	99.84528	99.3830311	0.46511852
11	55.0	99.8127888	99.321544	0.49460047
12	60.0	99.7772032	99.2600949	0.52096296
13	65.0	99.7385232	99.1986838	0.54420017
14	70.0	99.6967488	99.1373107	0.56430631
15	75.0	99.65188	99.0759756	0.58127554
16	80.0	99.6039168	99.0146784	0.59510205
17	85.0	99.5528592	98.9534192	0.60578001
18	90.0	99.4987072	98.8921978	0.61330356
19	95.0	99.4414608	98.8310144	0.61766688
20	100.0	99.38112	98.7698687	0.6188641
21	105.0	99.3176848	98.708761	0.61688936
22	110.0	99.2511552	98.647691	0.61173679
23	115.0	99.1815312	98.5866588	0.60340053
24	120.0	99.1088128	98.5256643	0.59187467
25	125.0	99.033	98.4647076	0.57715334
26	130.0	98.9540928	98.4037887	0.55923064
27	135.0	98.8720912	98.3429074	0.53810066
28	140.0	98.7869952	98.2820637	0.51375749
29	145.0	98.6988048	98.2212578	0.48619521
30	150.0	98.60752	98.1604894	0.45540789
31	155.0	98.5131408	98.0997586	0.4213896
32	160.0	98.4156672	98.0390654	0.3841344
33	165.0	98.3150992	97.9784098	0.34363634
34	170.0	98.2114368	97.9177917	0.29988947
35	175.0	98.10468	97.857211	0.25288781
36	180.0	97.9948288	97.7966679	0.2026254
37	185.0	97.8818832	97.7361622	0.14909627
38	190.0	97.7658432	97.675694	0.092294417
39	195.0	97.6467088	97.6152632	0.03221386
40	200.0	97.52448	97.5548697	0.031151405

Tabla N°1 Disminución de la concentración de carbono-14 en un fósil en los primeros 200 años después de la muerte del organismo, Fuente: Elaboración propia.

En la tabla N°1 se evidencia como disminuye la concentración porcentual de C-14 respecto al C-14 presente en la atmósfera en los primeros 200 años del fósil, se observan los valores obtenidos mediante el método numérico de Runge-Kutta de 4° orden (RK4) y su comparación con la solución exacta obtenida al resolver la ecuación diferencial ordinaria mediante el análisis matemático, la última columna muestra el error porcentual de la aproximación mediante el método numérico; según los datos se puede observar que el método RK4 tiene un alto grado de precisión pero a medida que nos vamos alejando de la fecha de origen el error porcentual tiende a crecer. Gráficamente este hecho puede observarse en la siguiente imagen:

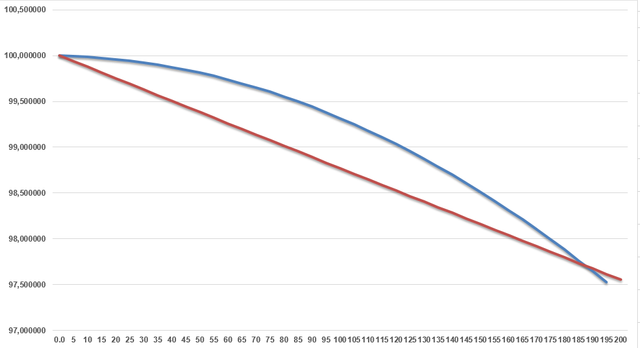
Disminución en la concentración de C-14 en los primeros 200 años del fósil. Comparación entre la solución exacta (Rojo) y las solución numérica (Azul). Fuente: Elaboración propia.

CONCLUSIONES Y OBSERVACIONES

1. El fechado mediante la técnica del isótopo carbono-14 es una de las técnicas clásicas de datación de fósiles, sin embargo, en la actualidad se han desarrollado nuevas técnicas isotopicas que utilizan al argón-40 y al potasio-40 obteniendo niveles de precisión más elevados.

2. En ciertos casos se pueden utilizar técnicas de datación de fósiles no isotopicas basadas en el uso de aminoácidos (racemización de aminoácidos).

3. El método numérico de Runge-Kutta de 4° Orden (RK4) tiene una gran precisión a la hora de obtener aproximaciones numéricas a los resultados de una ecuación diferencial ordinaria, muchas veces en la práctica estas aproximaciones son suficientemente cercanas para ser usadas como valores reales.

4. El método de Runge-Kutta de 4° Orden (RK4) tiene un grado de precisión mayor que el método de Euler debido a que utiliza el promedio ponderado de 4 pendientes en lugar del valor de una sola pendiente.

REFERENCIAS BIBLIOGRÁFICAS Y MATERIAL CONSULTADO PARA LA ELABORACIÓN DE ESTE ARTÍCULO

1. Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editoria Limusa Willey.

2. Chang (2003) Química 7° Edición, Editorial McGraw-Hill pág. 530 y 919

3. González (2018) Modelado matemático mediante ecuaciones diferenciales ordinarias aplicado al estudio de la dinámica de poblaciones de un sistema depredador-presa (especies presentes en el cerro Santa Ana). Disponible en el siguiente enlace.

4. Sauer (2013), Análisis Numérico. 2da edición Editorial Pearson.

5. Zill y Cullen (2008) Ecuaciones Diferenciales, 3° Edición, Editorial McGraw-Hill pág. 95-98.

Imagen de Dominio Público. Elaborada por @carloserp-2000 y @iamphysical.