La formación de ondas estacionarias está presente en una gran variedad de fenómenos físicos que abarcan distintas disciplinas como la acústica, la óptica, la electrodinámica y fenómenos cuánticos. Su análisis y comprensión permiten explicar y modelar sistemas en los que encontramos patrones ondulatorios definidos por este comportamiento.
Introducción
Cuando dos o más ondas se desplazan en un medio, la onda resultante en esa región es obtenida a partir de la suma de las funciones individuales que describen el comportamiento ondulatorio de cada una de ellas. Esta operación de suma es conocida como el principio de superposición, cuya aplicación es válida siempre que las ecuaciones que gobiernan el fenómeno sean de tipo lineal.
En esta oportunidad analizaremos el caso particular de la superposición de ondas atrapadas entre dos puntos conocidas como ondas estacionarias, las cuales son originadas por incidencias y reflexiones múltiples entre dichos puntos y donde el fenómeno de interferencia constructiva y destructiva determina los máximos y mínimos de la onda resultante.
Para esta demostración recrearemos el Experimento de Melde que se ilustra en la siguiente imagen.
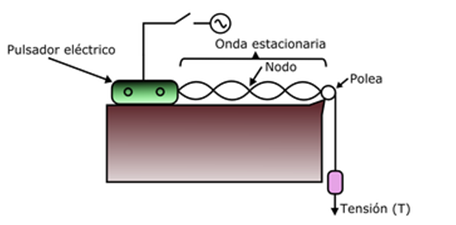 Figura 1. Experimento de Melde
Figura 1. Experimento de Melde
A continuación se muestra un análisis teórico y experimental donde se describen y comparan las variables presentes de una onda estacionaria.
Fundamentos teóricos
Para el desarrollo teórico se considera el caso de una región limitada por dos extremos fijos separados una longitud “L”, donde la onda incidente en uno de sus extremos genera una onda reflejada invertida con características idénticas.
Las funciones de onda y1 y y2 representan la onda incidente y reflejada:
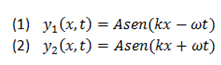
Según el teorema de superposición:
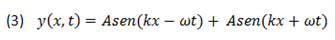
La onda resultante es de la forma:
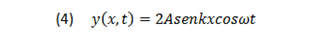
A→ Amplitud de las ondas
k→ Numero de onda
ω→Frecuencia angular
En la onda resultante obtenida se puede apreciar que su amplitud definida por el término "2Asenkx" indica que cada punto del medio oscila con una amplitud distinta, en el que sus desplazamientos máximos y mínimos cumplen con las siguientes condiciones:
- Condición de Puntos Mínimos (también llamados nodos):
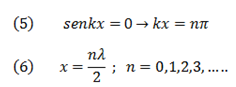
- Condición de Puntos Máximos (también llamados antinodos):
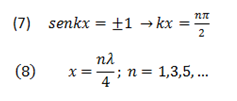
En los límites de la región seleccionada existe una condición de mínimo (nodo) en los extremos.
Si x = L , la ecuación (6) se expresa como:
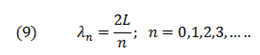
La ecuación (9) permite obtener los patrones de onda o modos de vibración para los distintos valores de “n” que se observarán en la longitud “L”.
Dado que la frecuencia es una función de la velocidad y de la longitud de onda podemos determinar las frecuencias asociadas a los distintos modos a partir de la ecuación:
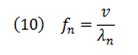
Donde la velocidad en un medio lineal está dada por:
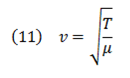
T→ Tensión aplicada
μ→densidad lineal del medio

De las ecuaciones (9), (10) y (11) se obtiene:
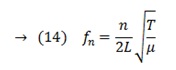
Las frecuencias obtenidas por la ecuación (14) genera una serie armónica en el que cada frecuencia es un múltiplo de la frecuencia correspondiente a n=1.
Parte experimental (formación de ondas estacionarias en el laboratorio)
Materiales y equipos utilizados
- Generador de señales
- Vibrador
- Cuerda elástica
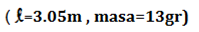
- Masa colgante (M=100 gr)
- Soportes
- Poleas
- Osciloscopio
- Cables coaxial caimán
Metodología utilizada
En el montaje que se muestra en la figura 2, el generador de señales se conecta al amplificador y al vibrador en el que se producen pequeñas perturbaciones a una frecuencia determinada. Estas perturbaciones se propagan a lo largo de la cuerda recorriendo una distancia “L” hasta el otro extremo fijo, donde una masa colgante ejerce una tensión sobre la cuerda de magnitud igual a su peso.
Las múltiples incidencias y reflexiones originan, según sea la frecuencia de resonancia, los patrones o modos de vibración que están en concordancia con la ecuación (14).
Las ondas estacionarias se observaran cuando la frecuencia del vibrador coincida con alguna de las frecuencias de la serie armónica.
 Figura 2. Visualización del patrón de ondas estacionarias para n=3.
Figura 2. Visualización del patrón de ondas estacionarias para n=3.
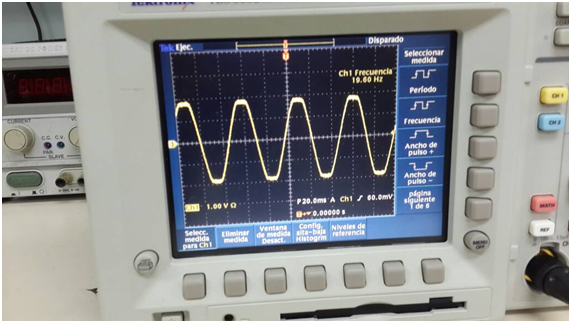 Figura 3. Lectura de la Frecuencia de resonancia experimental aplicada al vibrador (n=3).
Figura 3. Lectura de la Frecuencia de resonancia experimental aplicada al vibrador (n=3).
 Figura 4. Visualización del patrón de ondas estacionarias para n=2.
Figura 4. Visualización del patrón de ondas estacionarias para n=2.
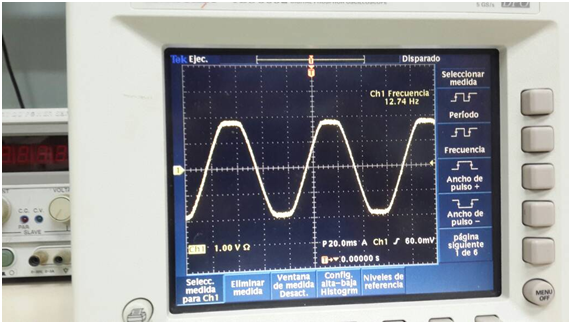 Figura 5. Lectura de la Frecuencia de resonancia experimental aplicada al vibrador (n=2).
Figura 5. Lectura de la Frecuencia de resonancia experimental aplicada al vibrador (n=2).
Cálculos y resultados
Para la obtención de las frecuencias de resonancia teóricas se deben calcular previamente con los datos disponibles la densidad lineal del medio y la tensión en la cuerda a través de las ecuaciones (12) y (13) respectivamente.
Una vez obtenidos estos valores se procede al cálculo de las frecuencias teórica usando la ecuación (14) para cada uno de los modos de vibración observado, los cuales son comparados con las frecuencias experimentales mostradas en las figuras 3 y 5. Estos cálculos y resultados son visualizados en la tabla 1y 2.
 Tabla 1. Resultado de la densidad lineal y tensión en la cuerda.
Tabla 1. Resultado de la densidad lineal y tensión en la cuerda.
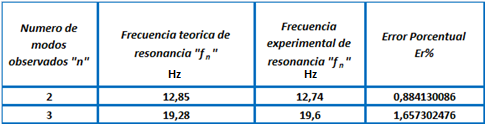 Tabla 2. Resultados de las frecuencias teóricas y porcentajes de error.
Tabla 2. Resultados de las frecuencias teóricas y porcentajes de error.
Conclusiones
Los pequeños márgenes de error obtenidos entre las frecuencias teóricas y experimentales validan la aplicación de los principios teóricos en los que se fundamenta las ondas estacionarias y evidencian los fenómenos de interferencia existentes en la propagación de las ondas mecánicas tal como lo estableciera Melde. La aplicación de los conceptos aquí expuestos no está limitada a problemas mecánicos. Este análisis puede extenderse a modelos donde las ondas que definen el comportamiento del sistema son de tipo electromagnético o en la descripción de funciones de ondas asociadas a partículas subatómicas cuyo comportamiento sea de tipo estacionario.
Referencias
Física para la Ciencia y la Tecnología. Tipler Mosca. Volumen 1: Mecánica. Oscilaciones y ondas. Termodinámica. 5a edición. Editorial Reverté.
Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo I. McGraw-Hill.
Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 1. Addison Wesley Longman.
Física para Ciencias e Ingeniería. Fishbane, Gasiorowicz, Thornton. Volumen I. Prentice Hall.

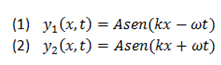
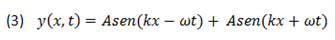
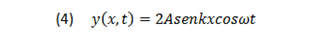
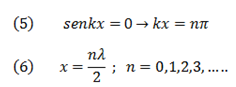
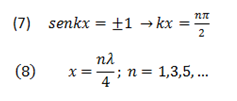
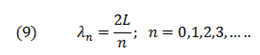
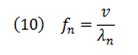
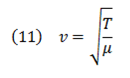

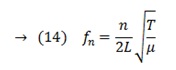
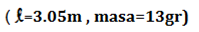






Siendo un SteemStem Estados
La utilización de equipos avanzados para explicar un fenómeno físico es imprescindible a la hora de impartir conocimientos a los estudiantes de ciencias. Buen trabajo mi estimado @lorenzor
Gracias estimado @iamphysical, ciertamente las herramientas actuales contribuyen enormemente en lograr nuestros objetivos en la enseñanza ya que facilitan la visualización y verificación de los fenómenos físicos.
Gracias por leer y comentar. Mi satisfacción y agradeciendo por el apoyo. Estaré compartiendo otras publicaciones. Feliz dia
Gracias por esta información estimado profesor @lorenzor. Resulta agradable saber que aun hacemos ciencia, sin importar la situación actual. Sigamos cultivando ciencia.
Muy buen artículo @lorenzor. Gracias por compartirlo.
Saludos!.
Hola, buen post. Saludos