ESTUDIO DE LAS APLICACIONES DEL ANÁLISIS MATRICIAL EN LA OBTENCIÓN DE LA MATRIZ DE RIGIDEZ DE UN PÓRTICO PLANO
INTRODUCCIÓN
En el análisis estructural, el uso de métodos matriciales, entra en juego, cuando nos topamos con sistemas que posean más de un grado de libertad tanto estático como dinámico. La diferencia entre uno y otro, estriba en el hecho de que los grados de libertad estáticos son las coordenadas necesarias para definir la posición de una junta, y la cantidad de estos incide directamente en el tamaño de la matriz de rigidez. Por su parte los grados de libertad dinámicos, son aquellas coordenadas necesarias, para definir la ubicación de las masas; y por consiguiente inciden en el tamaño de la matriz de masa.
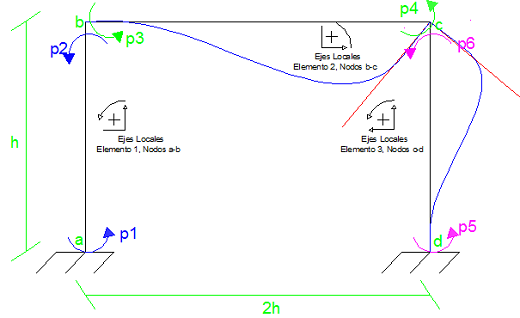
Dado que los grados de libertad estáticos son responsables del tamaño de la matriz de rigidez, conviene representar el caso base de estudio, que estaremos abordando, el cual se encuentra ilustrado en la imagen N°01.
Imagen N°01: pórtico plano, configuraciones deformadas, matriz de rigidez “K”
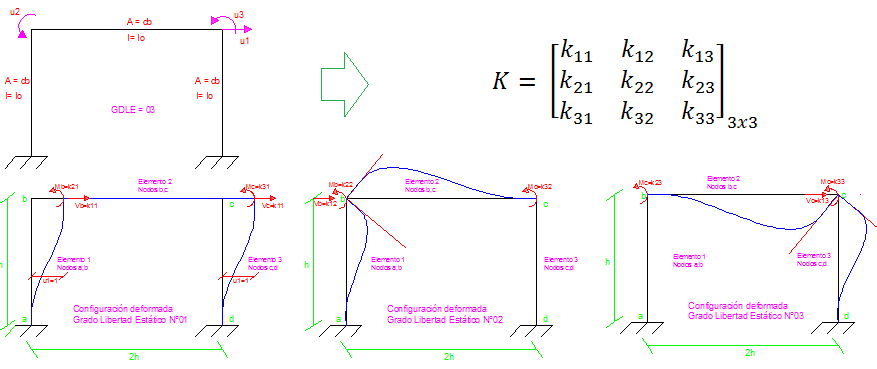
Fuente: Santana (2018)
Como se puede apreciar, se trata de un pórtico plano de un solo nivel, constituido por tres barras de sección constante, las cuales se suponen infinitamente rígidas en dirección axial( A = ∞), es decir, no sufren acortamiento ni alargamiento; pero si deformación transversal (I=Io) producto de la rotación de los nodos b y c. De tal manera, que el sistema mostrado, se puede discretizar con 3 grados de libertad estáticos, cuya configuración deformada para cada uno de ellos, la podemos apreciar en la imagen N°01, y en estas deformaciones se considera la hipótesis de que el sistema está en el rango elástico-lineal; lo cual es la base, de los métodos de obtención de matriz de rigidez que estaremos estudiando.
El hecho de poseer tres grados de libertad estáticos sugiere que el tamaño de la matriz sea de 3X3, correspondiendo cada columna de la matriz, a la configuración deformada perteneciente a cada grado de libertad estático. Los sub-índices de cada uno de los elementos de la matriz, pueden ser interpretados genéricamente de la siguiente forma: kij, fuerzas aplicadas en la coordenada “i” que producen un desplazamiento en la dirección “j”, de tal manera que “j” hace alusión a los grados de libertad estáticos.
En este trabajo aprenderemos a obtener la matriz de rigidez, aplicando en primera instancia los “coeficientes de rigidez para un elemento en flexión” y el “método de los desplazamientos”, demostrando como con la aplicación de ambos métodos se llega al mismo resultado.
BASES CONCEPTUALES QUE RIGEN EL USO DE LOS COEFICIENTES DE RIGIDEZ PARA UN ELEMENTO A FLEXIÓN
Los elementos que conforman el caso en estudio (vigas y columnas), se rigen por una condición en común, referida al hecho de que no sufren deformación axial (acortamiento-alargamiento); y esto queda muy bien ilustrado en el diagrama de cuerpo libre de la imagen N°02.
Imagen N°02: elemento de sección constante, axialmente indeformable
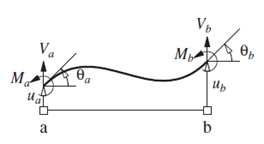
Fuente: Chopra, 2014
Según Chopra (2014), los momentos de flexión (Ma, Mb), y las fuerzas cortantes (Va y Vb) se calculan a partir de ua-ub y θa-θb, a través de las siguientes expresiones:
Cuando se está en presencia de un elemento vertical, el autor propone la siguiente adaptación:
Imagen N°03: elemento vertical de sección constante, axialmente indeformable
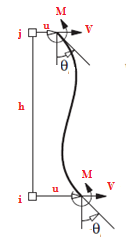
Fuente: Chopra (2014) adaptado por Santana (2018)
Las expresiones de momentos flexionantes y fuerzas cortantes, ajustadas a la imagen N°03 quedan de la siguiente forma:
EJEMPLO DE APLICACIÓN DE LOS COEFICIENTES DE RIGIDEZ PARA UN ELEMENTO A FLEXIÓN
El sistema mostrado, está constituido por tres barras, de las mismas propiedades en cuanto Área “A”, Inercia “I” y módulos de elasticidad “E”. Se utiliza la nomenclatura u1, u2, u3, para ilustrar los tres grados de libertad estáticos, responsables de las tres configuraciones deformadas de la estructura.
Imagen N°04: pórtico plano en estudio
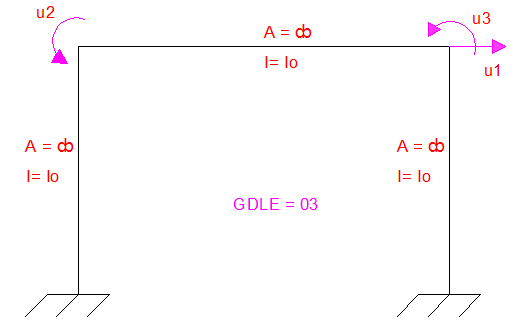
Fuente: Santana (2018)
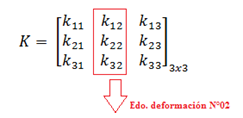
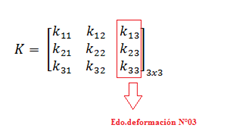
La matriz de rigidez a obtener presenta la siguiente forma:
Planteemos ahora los estados de deformación, destacando que en cada uno de ellos los elementos que aportan a la rigidez K de la estructura, son aquellos que sufren deformación transversal.
ESTADO DEFORMACIÓN N° 01
Para lograr el estado de deformación N°01, asignamos un desplazamiento unitario, en la dirección indicada por el grado de libertad estático “u1”, surgiendo el siguiente vector de desplazamiento-rotación:
La configuración deformada se puede apreciar en la siguiente imagen. En la misma, se indican también los elementos a obtener de la matriz de rigidez, contenidos en la primera columna de esta:
Imagen N°05: configuración deformada “u1”
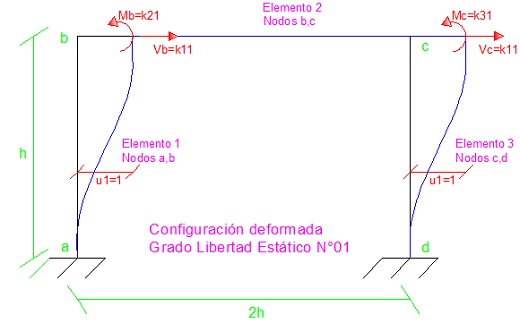
Fuente: Santana (2018)
En cada estado de deformación, los elementos que contribuyen a la rigidez son aquellos que sufren deformación. Tomando como referencia el elemento N°01 (ver imagen N°05), para el uso de los coeficientes de rigidez a flexión, se tiene que:
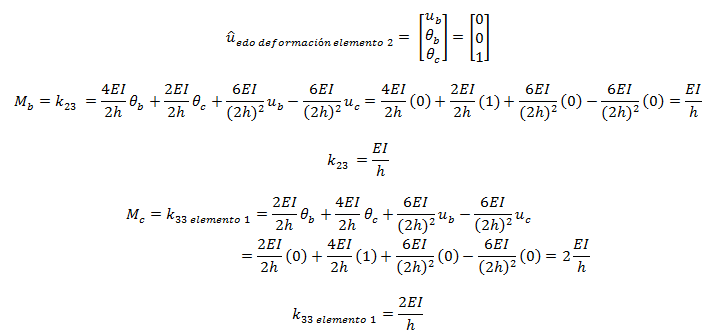
En lo que respecta al elemento N°02, se tiene:
Los elementos de la primera columna de la matriz de rigidez son:
ESTADO DEFORMACIÓN N° 02
Para lograr el estado de deformación N°02, asignamos una rotación unitaria, en la dirección indicada por el grado de libertad estático u2, surgiendo el siguiente vector de desplazamiento-rotación:
La configuración deformada se puede apreciar en la imagen N°06. Y se resaltan los elementos a obtener de la matriz para este estado de deformación, pertenecientes a la segunda columna de la matriz K:
Imagen N°06: configuración deformada “u2”
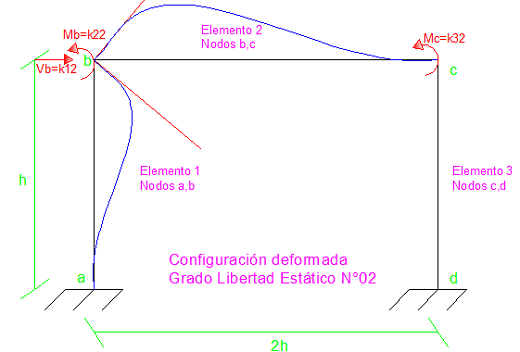
Fuente: Santana (2018)
Para el elemento N° 01, se tiene:
Para el elemento N° 02, se tiene:
Los elementos de la segunda columna de la matriz de rigidez son:
ESTADO DEFORMACIÓN N° 03
Para lograr el estado de deformación N°03, asignamos una rotación unitaria, en la dirección indicada por el grado de libertad estático “u3”, surgiendo el siguiente vector de desplazamiento-rotación:
La configuración deformada se puede apreciar en la imagen N°07. Y se resaltan los elementos a obtener de la matriz para este estado de deformación, pertenecientes a la tercera columna de la matriz K.
Imagen N°07: configuración deformada “u3”
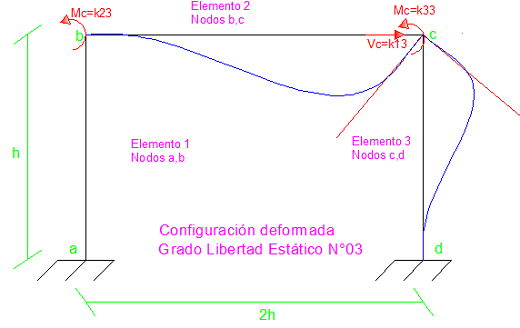
Fuente: Santana (2018)
Para el elemento N°02, se tiene lo siguiente:
Para el elemento N°03, se tiene lo siguiente:
Los elementos de la tercera columna de la matriz de rigidez son:
Agrupando todos los resultados obtenidos para cada estado de deformación, se construye la matriz de rigidez de la forma:
La matriz K obtenida, se puede rescribir de la siguiente forma:
BASES CONCEPTUALES QUE RIGEN EL USO DEL MÉTODO DE LOS DESPLAZAMIENTOS
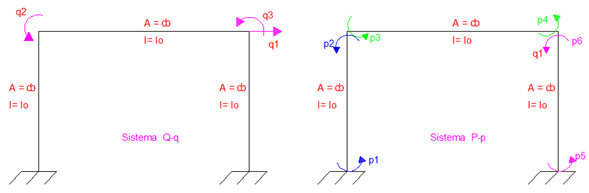
La aplicación del método de los desplazamientos en esencia sigue la misma filosofía de establecer distintos estados de deformación en concordancia con los grados de libertad estáticos que posea la estructura que se analiza. Sin embargo la forma de representar este aspecto, es con el planteamiento de un sistema de coordenadas generalizadas (Q-q), como se muestra a continuación, ajustado al caso en estudio.
Imagen N°08: Sistema Q-q, para la aplicación del método de los desplazamientos
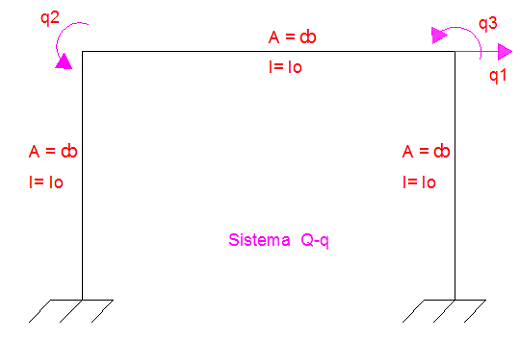
Fuente: Santana (2018)
En lo referente a los tipos de deformaciones permitidas en los elementos, que dependen de las propiedades de inercia y de área de los mismos, se plantea un sistema P-p, como el que se muestra a continuación, ajustado también al caso en estudio:
Imagen N°09: sistema P-p, para la aplicación del método de los desplazamientos
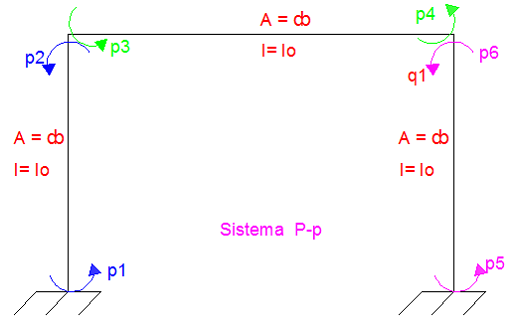
Fuente: Santana (2018)
Como se aprecia en la imagen N°09, los elementos pueden sufrir deformaciones transversales, indicadas por el símbolo “p” y tienen impedidas las deformaciones axiales, dado que son elementos de área infinita, es decir, no se pueden acortar ni alargar. Partiendo de las propiedades de cada elemento, en cuanto inercia y área McGuire-Gallagher (1979), señala para el caso de un elemento de sección constante, las siguientes idealizaciones:
Imagen N°10: caso N°01, A=Ao, I=Io, elemento de sección constante
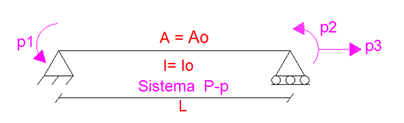
Fuente: McGuire-Gallagher (1979) adaptada por Santana (2018)
La sub-matriz “k” asociada a este caso es la siguiente:
Imagen N°11: caso N°02, A=∞,I=Io, elemento de sección constante
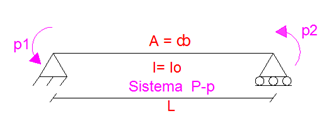
Fuente: McGuire-Gallagher (1979) adaptada por Santana (2018)
La sub-matriz “k” asociada a este caso es la siguiente:
Imagen N°12: caso N°03, A=Ao,I=∞, elemento de sección constante
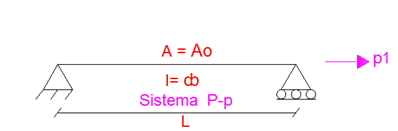
Fuente: McGuire-Gallagher (1979) adaptada por Santana (2018)
La sub-matriz “k” asociada a este caso es la siguiente:
Finalmente, es importante comentar sobre un concepto de mucha importancia en la aplicación del método de los desplazamientos como lo es la deformación como cuerpo rígido de un elemento estructural, lo cual se ilustra en la imagen N°13.
Imagen N°13: idealización del concepto de rotación como cuerpo rígido "Ψ".
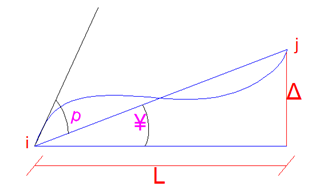
Fuente: Santana (2018)
En la imagen mostrada, se encuentra un elemento de longitud “L”, que sufre una rotación como cuerpo rígido"Ψ"; basándonos en la hipótesis de desplazamientos infinitesimales, la deformación como cuero rígido se puede calcular de la siguiente manera:
Por otro lado, se aprecia la deformación transversal “p” que sufre el elemento estructural, lo cual en conjunto con la rotación como cuerpo rígido, representa la rotación total en el nodo, correspondiente al grado de libertad estático, es decir:
Conociendo θi , que obedece a la rotación correspondiente al vector que rige una determinada configuración deformada, y Ψ, que es la deformación como cuerpo rígido, podemos calcular los valores de p, de la forma:
EJEMPLO DE APLICACIÓN DEL MÉTODO DE LOS DESPLAZAMIENTOS
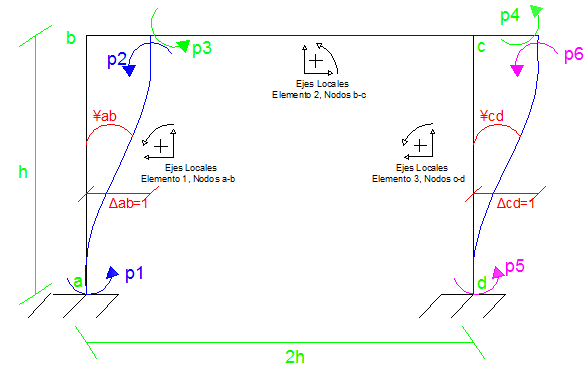
Se trabaja con el mismo pórtico utilizado en la aplicación de los coeficientes de rigidez para elementos a flexión, a los fines de contrastar resultados en cuanto a la matriz de rigidez “K” obtenida. A continuación, planteamos los sistemas Q-q y P-p
Imagen N°14: representación de los sistemas Q-q y P-p
Fuente: Santana (2018)
Procedemos a establecer los distintos estados de desplazamiento:
ESTADO DE DESPLAZAMIENO N°01
El vector desplazamiento “q” viene dado por:
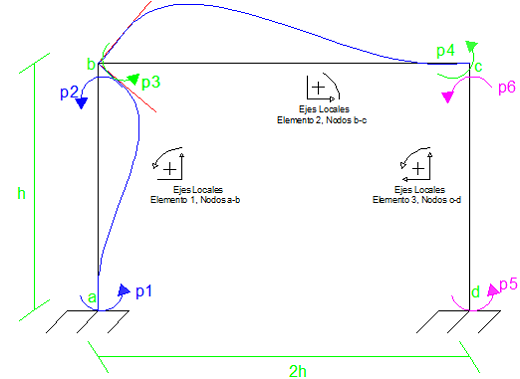
Imagen N°15: configuración deformada, estado de desplazamiento N°01
Fuente: Santana (2018)
Tabla N°01: resumen de cálculos para el estado de desplazamiento N°01

Fuente: Santana (2018)
Los valores de “p” obtenidos para cada elemento se agrupan de la siguiente manera:
ESTADO DE DESPLAZAMIENO N°02
El vector desplazamiento “q” viene dado por:
Imagen N°16: configuración deformada, estado de desplazamiento N°02
Fuente: Santana (2018)
Tabla N°02: resumen de cálculos para el estado de desplazamiento N°02

Fuente: Santana (2018)
Los valores de “p” obtenidos para cada elemento se agrupan de la siguiente manera:
ESTADO DE DESPLAZAMIENO N°03
El vector desplazamiento “q” viene dado por:
Imagen N°17: configuración deformada, estado de desplazamiento N°03
Fuente: Santana (2018)
Tabla N°03: resumen de cálculos para el estado de desplazamiento N°03

Fuente: Santana (2018)
Los valores de “p” obtenidos para cada elemento se agrupan de la siguiente manera:
Procedemos a ensamblar los vectores “p” obtenidos para cada estado de desplazamiento, los cuales representan las columnas de la matriz que se construye a continuación:
La matriz A transpuesta es:
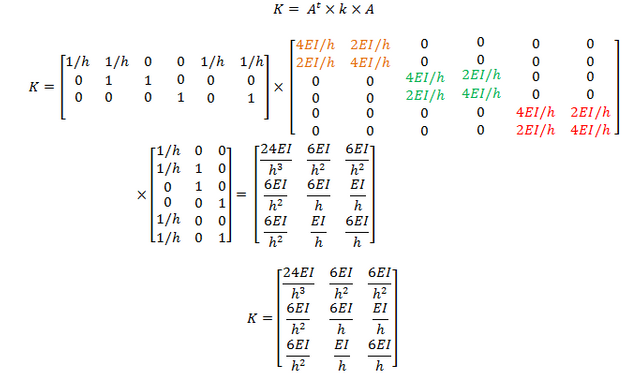
Obtenemos ahora la matriz “k”, para lo cual se realiza el ensamblaje de las sub-matrices obtenidas para cada elemento, que se ajustan al caso N°2 (ver imagen N°11).
Finalmente la matriz de rigidez “K” se obtiene de la siguiente forma:
Llegando al mismo resultado de la aplicación de los coeficientes de rigidez a flexión.
CONCLUSIONES SOBRE LAS PROPIEDADES DE LA MATRIZ DE RIGIDEZ
1.- El tamaño de la matriz de rigidez está condicionada a la cantidad de grados de libertad estáticos del sistema estructural.
2.- La matriz de rigidez es una matriz simétrica, y los elementos de la diagonal principal, siempre son valores positivos.
3.- El alcance de los métodos estudiados, es para sistemas que se encuentren en el rango elástico lineal y elementos de sección constante.
FUENTES CONSULTADAS
1.- CHOPRA ANIL K.DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACIÓN, MÉXICO 2014.
2.- MCGUIRE-GALLAGHER. MATRIX STRUCTURAL ANALYSIS, WILEY, NEW YORK 1979.
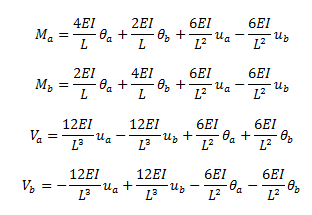
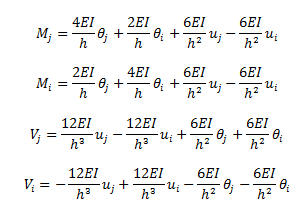
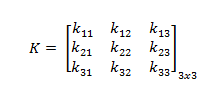
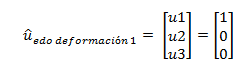



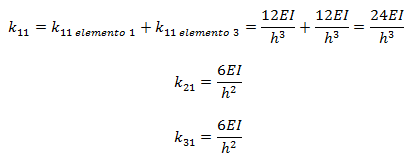
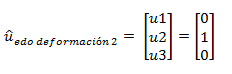


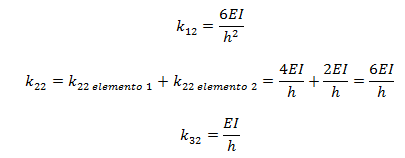
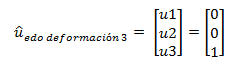

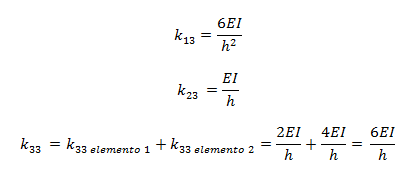
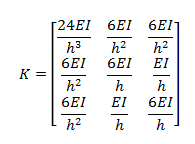
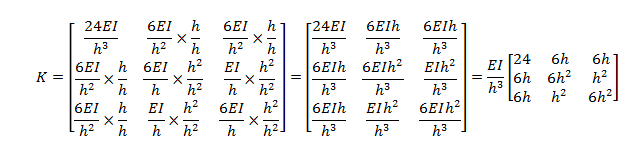
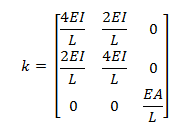
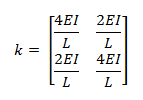
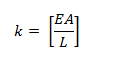
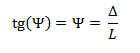
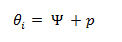
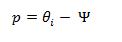
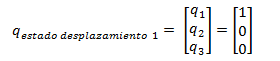
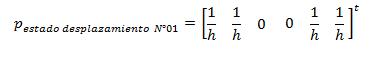

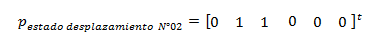

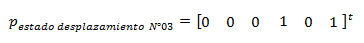
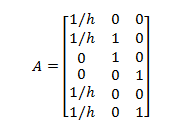


Being A SteemStem Member
Excelente tu desarrollo y análisis matemático para un problema real de rigidez. La adecuación que haces a cada caso usando las imágenes ha sido una clase magistral para entender el problema!
Gracias @iamphysical, las imágenes son un excelente recurso didáctico en la gestión del aprendizaje.
Buen contenido amigo!
Gracias @ingenierogabriel.
Excelente análisis, buen uso de las herramientas matemáticas en el estudio de la rigidez
Gracias @ydavgonzalez, las aplicaciones de las matemáticas en el análisis matricial son impresionantes.