FÍSICA DEL ESTADO SÓLIDO: Introducción a los Semiconductores. TEMA CONVERSATORIO.

Hola de nuevo compañeros de #stem-espanol y #steemstem. Hoy me animé a compartir el contenido del conversatorio del día 03/05/2018 llevado a cabo en el canal de discord, el cual se tituló FÍSICA DEL ESTADO SÓLIDO: Introducción a los semiconductores.

Este conversatorio tenía como objetivo principal sumergirnos en el mundo de los Semiconductores desde el punto de vista de la Física. Se contó con la participación de mi persona "@djredimi2" como ponente, así como cada uno de los que conforman el canal de #stem-espanol en discord.app.

Imágen Presentación del tema conversatorio por @djredimi2.

El contenido está conformado por una sección conceptual y comparativa entre los materiales aisladores, conductores y semiconductores. Seguidamente, de una breve introducción a los procedimientos experimentales sobre la caracterización física de semiconductores.

---

I. SEMICONDUCTORES.

El semiconductor es una substancia cristalina que tiene una estructura de bandas de energía, en la que la banda de estados electrónicos (banda de valencia), está completamente llena, y se separa de la otra (banda de conducción) que está totalmente vacía al cero absoluto (T=0 °K), por medio de una región angosta de energías prohibidas. Mediante la Figura 1, vemos que en el cero absoluto, el semiconductor es un aislante perfecto, ya que cuenta con bandas totalmente llenas.

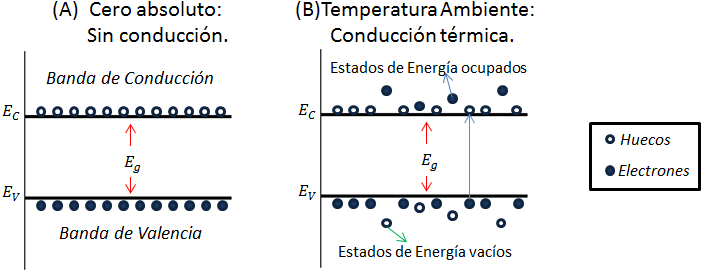
^{Figura 1. Ilustración del comportamiento de los electrones en bandas planas en función d ela temperatura. Fuente: Elaboración propia con el uso de Paint y Microsoft Power Point, Autor: Lic. Daiver Juarez.}

Sin embargo, a temperaturas más altas, algunos electrones de la banda de valencia pueden adquirir la suficiente energía térmica aleatoria para excitarse a través de la banda prohibida con el fin de convertirse en electrones de conducción en la banda de conducción que antes estaba vacía. Los estados vacíos de la banda de valencia pueden contribuir también a la conductividad comportándose como huecos positivamente cargados.

Es evidente que el número de electrones de conducción aumentará al incrementarse la temperatura, y por tanto, la conductividad eléctrica también aumentará.

1.1. Relación entre los semiconductores y los aislantes y metales.

Como no se puede obtener corriente eléctrica en bandas vacías o totalmente llenas, cualquier conductividad eléctrica que presente un cristal debido al movimiento de electrones libres, se debe al movimiento de los electrones dentro de las bandas de energía que están solo parcialmente llenas. Esta observación es la base de la diferencia entre los aislantes, los conductores metálicos y los semiconductores (Figura 2).

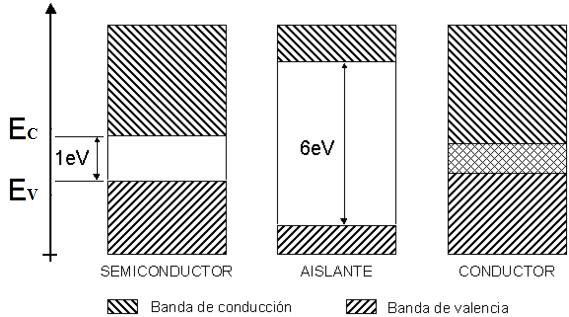
^{Figura 2. Diagrama de bandas comparativo entre los aislantes, semiconductores y conductores metálicos. Fuente: Wikipedia, Autor: Usuario Yrithinnd, Edición: Lic. Daiver Juarez.}

En un aislante, la región de energía prohibida es tan ancha que es prácticamente imposible, a temperaturas físicamente posibles, excitar térmicamente un número importante de electrones. Si el número de electrones de un cristal no basta para llenar por completo la banda de energía más elevada, sino que la deja llena en parte, muchos de ellos pueden comportarse como electrones libre y servir como carca o portadores de carga. Un cristal de esta índole presentará propiedades características de un conductor metálico. La conductividad eléctrica de un semiconductor es casi siempre menor que la de un metal debido a la concentración limitada de electrones libres y huecos y, además depende de la temperatura, así como también de la brecha de energía.

1.2. Tipos de Semiconductores.

1.2.1. Semiconductores intrínsecos.

Un semiconductor en el que los huecos y los electrones se crean exclusivamente mediante una excitación térmica a través de la banda prohibida de energía, se conoce como semiconductor intrínseco, Figura 1. Los huecos y los electrones creados de esta manera a menudo se denominan portadores intrínsecos de carga y la conductividad originada por estos portadores se llama conductividad intrínseca. En un semiconductor intrínseco, las concentraciones de electrones y huecos siempre serán las mismas, ya que la excitación térmica de un electrón origina inevitablemente solo un hueco.

1.2.2. Semiconductores extrínsecos.

Es muy fácil introducir cantidades muy pequeñas de substancias de elementos pertenecientes al grupo V de la tabla periódica, en cristales puros de Si o de Ge, como átomos de impurezas que ocupan sitios de la red que normalmente estarían ocupados por átomos del semiconductor covalente.

Tipo n.

Debido a que los átomos del grupo V tienen cinco electrones de valencia, cuatro de ellos se usan para formar enlaces covalentes y el quinto se enlaza al átomo de impureza sólo mediante fuerzas electrostáticas que son muy débiles. Entonces, átomo de impureza que queda se convierte en un ion positivo, que, sin embargo, es inmóvil. Esta situación se ilustra en la figura 3a. En cristales que contienen este tipo de impurezas existen más electrones que huecos. Estos cristales se denominan semiconductores tipo n, ya que la mayoría de los portadores de carga son electrones negativos. Los átomos del grupo V de substitución se llaman con frecuencia átomos donadores (dadores), ya que cada uno de ellos dona un electrón libre adicional al cristal.

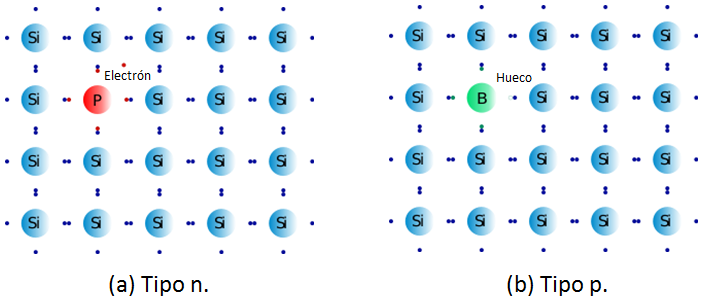
^{Figura 3. (a) Electrón libre originado por la ionización de un átomo de impureza de fosforo de substitución, (b) hueco libre producido por la ionización de un átomo de boro de impureza de substitución. Fuente Imagen (a): Wikipedia, Autor: Usuario Guillom. Fuente Imagen (b): Wikipedia, Autor: Usuario Guillom. Edición: Lic. Daiver Juarez.}

Tipo p.

Si en lugar de los átomos del grupo V se introducen en la red átomos de impurezas del grupo III, se observará un efecto distinto. Estos átomos tienen solo tres electrones de valencia que se usan para formar enlaces covalentes con tres átomos cercanos; pero el cuarto enlace siempre carece de un electrón. En efecto, existe un hueco adicional que se crea en la estructura del enlace covalente en el átomo de la impureza. En la figura 3b se ilustra esta situación. La energía necesaria para la migración del hueco lejos del sitio de la impureza es del orden de la energía que se requiere para eliminar el electrón adicional de un átomo donador. En cristales que contienen predominantemente este tipo de impurezas se tienen más huecos que electrones, aunque siempre habrá algunos electrones que se originan debido a la excitación térmica. Los cristales de esta índole se conocen como semiconductores tipo p, dado que los portadores de carga mayoritarios son positivos.

Cuando en un cristal semiconductor existen impurezas de ambos tipos, la conductividad es invariable mayor que la referente a un semiconductor puro o intrínseco a la misma temperatura, debido a los portadores de carga adicionales originados por los átomos de impurezas y, en general, mientras más grande es la concentración de impurezas, tanto mayor es la conductividad.

---

II. CARACTERIZACIÓN ESTRUCTURAL.

Debido a que el semiconductor es una substancia cristalina:

2.1. Sólido cristalino.

Para definir un sólido es necesario introducirse en la periodicidad geométrica del ordenamiento de los átomos o moléculas que componen a una substancia. Por ello, las substancias se consideran sólidas de acuerdo a la definición de: amorfas y cristalinas. En las substancias amorfas, los átomos y moléculas pueden estar enlazados con bastante firmeza entre sí, pero poseen poca o ninguna regularidad o periodicidad geométrica, en la forma en que los átomos están acomodados en el espacio. Estas substancias se consideran como líquidos sobre-enfriados.

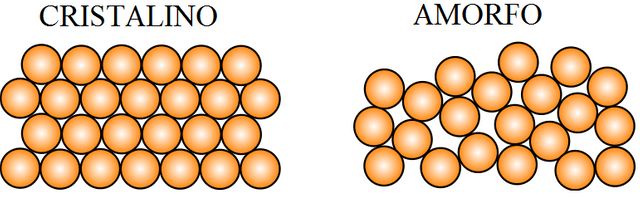
^{Figura 4. Substancia cristalina y amorfa. Fuente: Wikipedia, Autor: usuario Sbyrnes321, Edición: Lic. Daiver Juarez.}

Por otro lado, las substancias cristalinas se caracterizan por una periodicidad perfecta (o casi perfecta) en su estructura atómica; esta regularidad de estructura proporcionar un concepto muy simple de un cristal y facilita la tarea de comprender y calcular las propiedades físicas. Por esta razón, los sólidos cristalinos se comprenden mejor físicamente que los sólidos y líquidos amorfos. La perfección de dicha periodicidad en los cristales es bastante significativa, ya que la presencia de un número relativamente pequeño de imperfecciones (tales como átomos de impurezas, vacíos en la red o dislocaciones), puede producir cambios notables en el comportamiento físico del material.

2.2. Estructura cristalina y redes de Bravais.

La periodicidad geométrica de las substancias sólidas cristalinas es descrita mediante la estructura cristalina. Si tenemos una región del cristal definida por tres vectores, a, b y c, que al trasladarse por medio de cualquier múltiplo entero de dichos vectores pueda reproducirse una región similar del cristal, entonces tendremos una Celda Unitaria. La celda unitaria más pequeña (en volumen) que se puede definir para una sola red dada, se le conoce como Celda Primitiva. La figura 2 muestra la notación de las dimensiones y ángulos dentro de la celda unitaria.

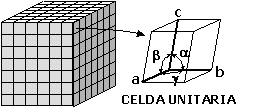
^{Figura 5. Dimensiones y ángulos de la celda unitaria. Fuente: Wikipedia, Autor: usuario Yrithinnd.}

Se puede demostrar que existen 14 formas generales de acomodar los puntos en las redes cristalinas, de tal modo que todos los puntos de dichas redes tengan exactamente el mismo medio circundante. Estas estructuras reticulares son conocidas como las redes de Bravais y se ilustran en la figura 6.

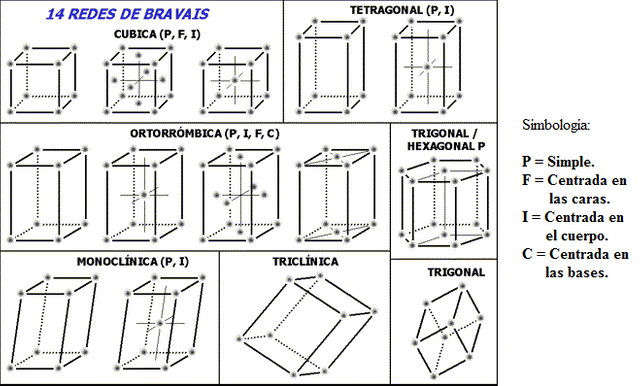
^{Figura 6. Redes de Bravais. Fuente: Wikipedia, Autor: usuario Magnus Manske, Editor: Lic. Daiver Juarez.}

En ocasiones es posible encontrar aparentemente otra configuración cristalina en un sólido. Esto se debe a una modificación ocasionada bien sea, por otra red cristalina superpuesta, o por la inclusión geométrica de otros puntos en la red.

La técnica experimental empleada para la obtención de los parámetros de la red cristalina es la "Difracción de Rayos X". En este post no se incluye su explicación, ya que para su desarrollo es necesario otro artículo.

---

3. CARACTERIZACIÓN ÓPTICA.

Debido a que tiene una estructura de bandas de energías:

3.1. Distribución del momento espacial.

Debido a que cada estado tiene definido energías asignadas, consideremos que dichos estados permitidos son distribuidos en momento espacial. La importancia de esta consideración es evidente ya que en las transiciones ópticas debemos conservar tanto la energía como el momento. Por lo que la energía cinética del electrón 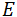es descrita en función del momento 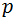por la relación:

Donde 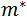es la masa efectiva del electrón, 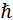es la constante de Dirac (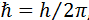, 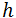la constante de Planck) y 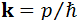es el vector de onda (también 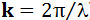). La figura 7 muestra como la energía de los electrones varía con el momento a lo largo de una dirección del momento espacial. Tal distribución es llamada valle parabólico.

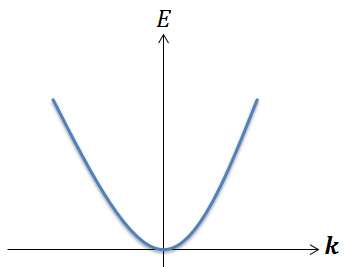
^{Figura 7. Dependencia entre Energía y Momento. Fuente: Elaboración propia con el uso de Paint y Microsoft Power Point, Autor: Lic. Daiver Juarez.}

3.1.1. Representación espacial de bandas para brechas directas.

En un momento espacial tridimensional, una superficie de energía constante forma una capa cerrada, con todo el incremento del momento, la energía de las siguientes capas incrementa cuadráticamente. A la banda inferior se le conoce como la banda de valencia. Y la banda superior, la banda de conducción, esto es mostrado en la figura 9. El significado de la curvatura hacia debajo de la banda de valencia es que si los electrones pudieran tener un movimiento neto (de no estar completamente llena la banda de valencia), los electrones serían acelerados en la dirección opuesta, a que si se estuvieran moviendo en la banda de conducción, es como si tuvieran masa negativa. Este tipo de representación de bandas se le conoce como bandas de brecha directa.

3.1.2. Representación espacial de bandas para brechas indirectas.

Ahora, este no es el único tipo de representación. Cuando la separación entre los átomos cercanos varia en las diferentes direcciones, la forma de la superficie de energía constante cambia a la de una esfera perfecta. Además, debido a las interacciones acumuladas desde la región cercana, y a todas las siguientes regiones cercanas, el mínimo del valle no se puede producir en 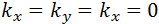, por lo que se tendrá que producir en otro punto de la dirección cristalográfica. Ejemplo la dirección cristalográfica [111] mostrada en la figura 10. Lo que permite por la simetría del cristal, de alguna distribución 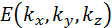que deba repetirse en todas las direcciones equivalentes.

3.2. Absorción Óptica.

Debido a la reflexión y absorción, su intensidad transmitida disminuye. Si consideramos las reflexiones en ambas superficies del material y la absorción [a], el comportamiento de la luz incidente que se transmite al atravesar un material puede ser explicado con la siguiente figura 8:

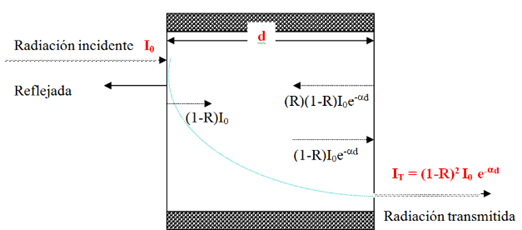
^{Figura 8. Transmisión de la luz a través de un material en el que se producen reflexiones en ambas superficies y hay absorción dentro de él. Fuente: [3], Autor: @iamphysical.}

En los semiconductores nos interesa analizar la configuración de las bandas de energía, por lo que se deben considerar todos los estados o niveles de energía que darán origen a estos procesos de absorción entre bandas: transición directa permitida, transición directa prohibida, transición indirecta, transición por excitones, transiciones desde la banda de impurezas, fonones longitudinales y acústicos, etc.

3.3. Transiciones directas entre la Banda de Valencia y la Banda de Conducción.

3.3.1. Transiciones directas PERMITIDAS.

La energía mínima de la banda de conducción, caracterizada por el vector de onda 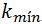, y la energía máxima de la banda de valencia, determinada por el vector de onda 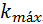, están dispuestas en un mismo punto de la zona de Brillouin, generalmente en el punto 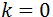, es decir, 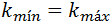. En la siguiente figura se muestra la representación de este proceso de absorción.

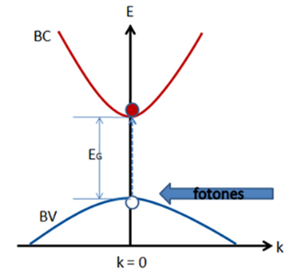
^{Figura 9. Absorción óptica fundamental para transiciones directas permitidas entre bandas. Fuente: [3], Autor: @iamphysical.}

Las transiciones de los electrones por la banda prohibida ocurrirán antes que nada entre estados energéticos, correspondientes al máximo de la banda de valencia (MBV) y al mínimo de la banda de conducción (mBC), donde el vector de onda 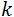es cero.

3.3.2. Transiciones indirectas entre bandas.

Existe un segundo grupo de materiales semiconductores en que los extremos de la banda de conducción y de la banda de valencia se encuentran para distintos valores de 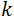, de manera que en este caso 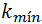es diferente 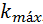. En la figura 11 se presenta el esquema para las transiciones indirectas entre bandas.

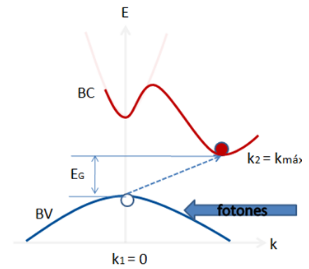
^{Figura 10. Transiciones ópticas en un semiconductor con bandas de energía complejas. Fuente: [3], Autor: @iamphysical.}

Aunque los procesos son más complicados por la emisión o absorción de fonones, la transición indirecta (de la figura 11) va desde el estado inicial 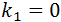hasta el final con .

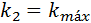La transmisión óptica o transmitancia (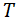) se determina por medio de la relación a partir de los valores de la intensidad transmitida (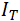) y la intensidad de radiación incidente (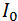), , 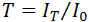obtenidos directamente de un espectrofotómetro. El coeficiente de absorción óptica 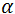por otro lado se calcula a partir de la ecuación:

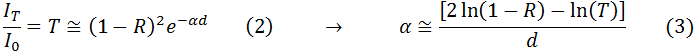
Donde 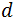es el espesor de la muestra y 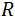es la reflectividad. En este punto es importante destacar que la absorción debe ser nula para la región de baja energía (), todos los espectros deben corregirse sustrayendo una pequeña absorción residual (Figura 6) aproximadamente constante en este rango del espectro. De esta manera se obtienen las curvas del coeficiente de absorción óptica en función de la energía.

Ahora bien, existen diferentes métodos para determinar el valor de la brecha de energía según el origen de las transiciones ópticas mencionadas anteriormente. Para transiciones directas permitidas que tienen una dependencia espectral de la forma [e,f]:

Donde 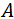es una constante que varía poco con la energía, 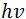es la energía del fotón incidente y 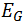es la brecha de energía.

---

El contenido también incluía una tercera parte donde se describe la Caracterización eléctrica de los semiconductores, pero decidí omitir esta sección por lo extendido del post. Espero en los siguientes días Mostrar en un post la importancia de este tópico ya que la electrónica de hoy día se basa en el principio de estos dispositivos del estado sólido.

Gracias por su atención. Se que los que participaron en el conversatorio podrán leer este post y recordar con agrado el conversatorio. Así mismo estaré emocionado por sus prontas ponencias en los siguientes conversatorios.

Hasta la próxima.

---

ALGUNAS REFERENCIAS.

[1] Mckelvey, John P. (1976). Física del estado sólido y de semiconductores. México. Editorial Limusa. P.13-18 y P.269-284.
[2] Pankove, Jacques I. (1971). “Optical Processes in Semiconductors”. New York, USA. Dover Publications, Inc. P.34-36.
[3] @iamphysical. "¿Cómo determinar la brecha de energía en un semiconductor?". Fuente.
[4] Fox, Mark. (2001). “Optical Properties of Solids”. New York, USA. Oxford University Press Inc. P.3-6.

@djredimi2 Te invita a formar parte de la sub-comunidad #stem-espanol, compartiendo temas de interés en Ciencias, Tecnologías, Ingenierías y Matemáticas en idioma Español. Cabe destarcar que debes cumplir con las normas correspondientes, las cuales puedes ubicar en el perfil de @carloserp-2000, quien es miembro de la comunidad #steemstem.