THE SOLID ANGLE - PART 2 - BASIC BACKGROUND (CONTINUATION)

tsoldovieri (60)in #steemstem • 7 years ago

Regards Steemians!. The present post is the second of a series dedicated to showing in a clear and simple way the definition of SOLID ANGLE, presenting the necessary equations and mathematical definitions. The first can be found in:

https://steemit.com/steemstem/@tsoldovieri/the-solid-angle-part-1-basic-background

Image related to the definition of Solid Angle and its applications.

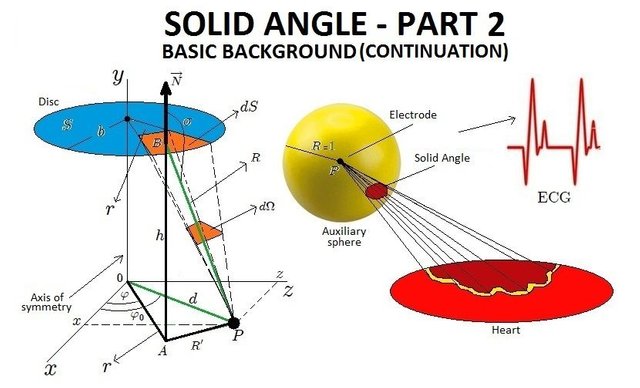
Continuing with the basic background for a good understanding of the definition of Solid Angle and how it is calculated, in this post I will talk about the Dihedral Angle, the Polyhedral Angle and the intersection of a polyhedral angle with a sphere.

THE DIHEDRAL ANGLE

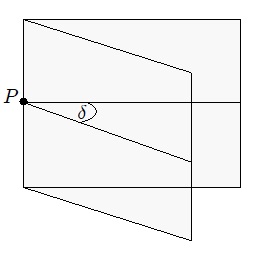
A Dihedral Angle is that formed by the intersection of two planes, as shown in Figure 1.

Figure 1 - Dihedral Angle of size δ.

The size of the dihedral angle is defined as the size of the angle (in Figure 1 is δ) formed between two straight lines, one in each plane, that intersect each other at a point P and are perpendicular to the edge along the which intersect the two planes. In other words, it is the size of the smallest possible angle that makes up two straight lines belonging to each plane.

THE POLYHEDRAL ANGLE

A Polyhedral Angle is the part of the space bounded by several non-coplanar plane angles, with common vertex V and shared sides (each side is common to two angles) as, for example, the polyhedral angle shown in figure 2.

Figure 2 - Polyhedral Angle.

The plane angles are called faces, the sides are called edges and the vertex of the angles is called the vertex of the polyhedral angle. Two consecutive faces form a dihedral angle. The simplest polyhedral angle is a trihedral angle, which is formed by three faces.

The conical surface formed by infinite rays of common end and pass through the closed curve C, it is also considered polyhedral angle (see figure 3). It is equivalent to a polyhedral angle of infinite faces.

Figure 3 - Angle Polyhedron formed by infinite rays that start from point V (vertex) and pass through the closed curve C.

The polyhedral angles can be convex and concave:

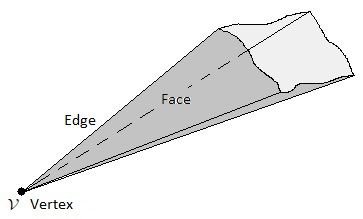
The Convex: is the polyhedral angle that remains in the same half-space with respect to the planes of each of its faces.
The Concave: is the polyhedral angle in which when extending the plane of one of its faces, a part of the angle is in a half-space and the rest in the other.

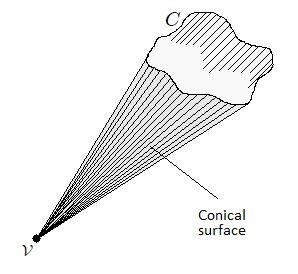
INTERSECTION OF A POLYHEDRAL ANGLE WITH A SPHERE

If a polyhedral angle is cut by the surface of a sphere of radius R with center at its apex, the intersecting surface is proportional to R².

Before continuing, it is necessary to define The homothety: is the transformation that makes correspond each point A of a figure another point A' (homologous of A) aligned with A and with center of homothety 0, so that:

Equation 1

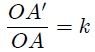
Here k is a non-zero constant, called Homothety Ratio.

Figure 3 - The intersection of a polyhedral angle with two spheres of radii R₁ and R₂ and centered at their vertex V respectively, generate two surfaces S₁ and S₂ that are homothetic.

When cutting the polyhedral angle by two spheres of radii R₁ and R₂ (see figure 4), the surfaces S₁ and S₂ are homothetic, therefore, they are proportional to the square of their homothetic ratio,

Equation 2

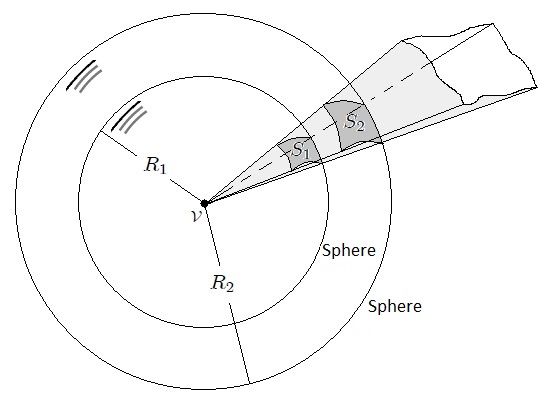
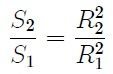
It is possible to find the surface S₁ as a function of only the surface S₂ and the radius R₂ of the sphere that defines this last surface. In effect, when doing 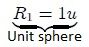Relación 1Ing.jpg (u is a unit of measure) in equation 2 you get,

Equation 3

and since this relation is general, then for any sphere of radius R₂ = R it is valid that,

Equation 4

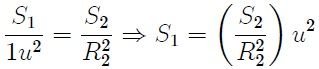
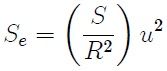
where 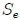Relación 3.jpg is the surface determined by the polyhedron angle on the surface of the unit sphere and S is the surface determined by the same angle on the sphere of radius R. Note that the quantity 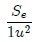Relación 2.jpg is dimensionless and numerically equal to 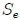. If this amount is called Ω then,

Equation 5

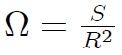
which is the key equation for the mathematical definition of solid angle.

In the case that more than two spheres are used, relations such as equation 2 will remain valid. In view of this, it is now possible to write that,

Equation 6

with n = 1,2,3, ..., up to the total number of spheres.

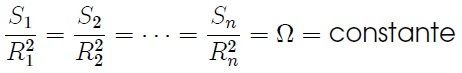
REFERENCES

Soldovieri, Terenzio & Viloria, Tony. EL ANGULO SOLIDO Y ALGUNAS DE SUS APLICACIONES. 1era edición (borrador). You can download it on my website http://www.cmc.org.ve/tsweb/
All the images presented here were elaborated by me. The color image constitutes a modification of the cover image of the text indicated above, of which i'm the author..
Moya de la T. D., A. PRINCIPIOS DE GEOMETRIA. Imprenta de D. Alejandro Gómez
Fuentenebro, 2da edition, 1864. pp. 67.
Alvarez C., E. ELEMENTOS DE GEOMETRIA, CON NUMEROSOS EJERCICIOS Y GEOMETRIA DEL COMPAS. Editorial Universidad de Medellín, 2003. pp. 368 - 370.
Izquierdo A., F. GEOMETRIA DESCRIPTIVA. Editorial Paraninfo, 24a edition, 1998. pp.
68 - 76.
Zuñiga P., M. L. POLIEDROS ARQUIMEDIANOS. Revista del Profesor de Matemáticas,
(6):49 – 57, 1998.
Puig A., P. CURSO DE GEOMETRIA METRICA - FUNDAMENTOS, volume 1. Biblioteca
Matemática S. L., Madrid - España, 11a edition, 1973. pp. 117 - 128.
Faget, J. & Mazzaschi, J. TEMAS PROGRAMADOS DE FISICA - GENERALIDADES, volumen 1. Editorial Reverté, S.A., 1976.

It is my wish that the present information can be very useful to all. The next in this series will refer to the Surface and its vector representation.
Sorry for my English!.
Until my next post. Regards! 😁