THE SOLID ANGLE - PART 1 - BASIC BACKGROUND

tsoldovieri (60)in #steemstem • 8 years ago (edited)

Regards Steemians!. The present is the first of a series of posts dedicated to showing, in a clear and simple way, the definition of SOLID ANGLE, presenting the necessary equations and mathematical definitions.

I will begin, in the first posts, with some basic knowledge necessary to reach the definition of Solid Angle. Some of its applications in the field of science will also be presented.

Image related to the definition of Solid Angle and its applications.

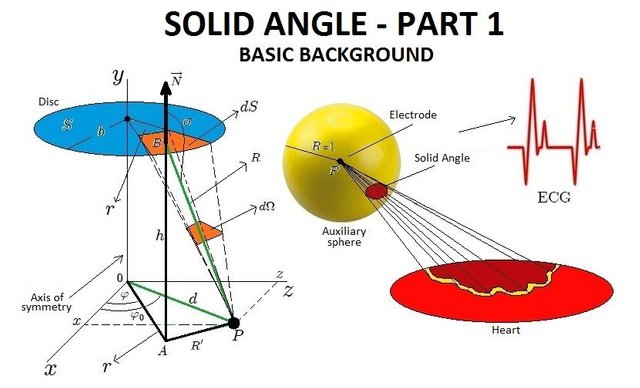
BASIC BACKGROUND

THE PLANE ANGLE

As will be seen later, the solid angle is the measure of an angle in space, so it is convenient to remember and understand how angles are measured in the plane.

A plane angle α is a measure of the aperture between two lines intersecting at a point.

Figur1 1 - Plane angle α subtended by a rectangle in the plane, with respect to a reference point P located in the same plane.

Suppose that the angle α is subtended by a plane figure in the plane, a rectangle for example, with respect to a point P in the same plane. This angle is obtained geometrically by drawing from P two straight lines L₁ and L₂ that touch the perimeter of the rectangle without ever going through its interior, as shown in the figure 1. To measure it, proceed as follows:

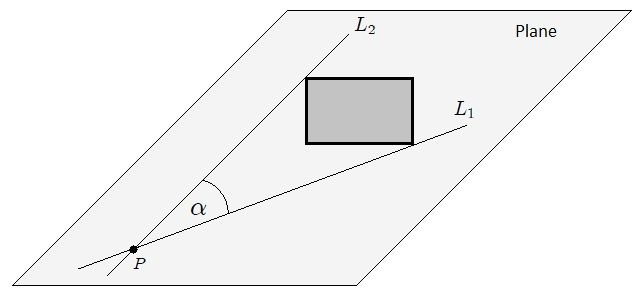
A circumference is superimposed on the lines L₁ and L₂, which is usually called Auxiliary Circumference, whose center coincides with point P as shown in Figure 2.

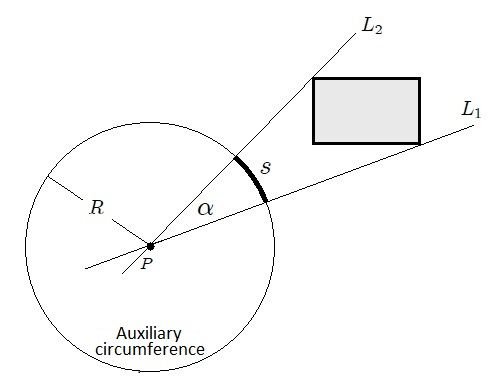
Figure 2 - Measurement of the plane angle α subtended by a plane figure with respect to a point P.
We proceed to measure the length s and the radius R of the arc that is limited by the two straight lines.
The measure of the angle α subtended by the two lines will be given by,
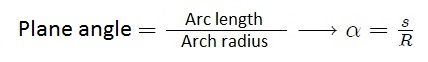
Equation 1

The portions of the line that limit the angle are called sides of the angle and the point of intersection P is called the vertex.

If an auxiliary circumference of radius R₁is plotted with center at the vertex of the angle α shown in Figure 3, an arc of length s₁ is obtained so that the quotient 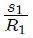results in the measure of α, as indicated by the equation 1. If a new auxiliary circumference of radius R₂ (with center at its vertex) is drawn for the same angle, an arc of length s₂ is obtained, giving the quotient 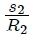the same measure α and so on. Hence,

Equation 2

Figure 3 - Each plane angle has the property indicated by the equation 2. For this reason α is used to identify each plane angle.

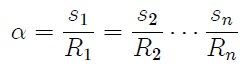
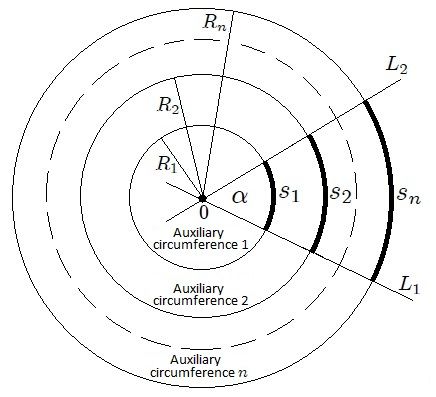
Whatever the size of the auxiliary circumference, equation 2 will remain constant for the same aperture between the lines.

However, when looking at Figure 2, it can be easily deduced that the angle α will decrease if the rectangle moves away from the point P.

The angle α as defined in equation 1 is dimensionless, since it is the quotient between two lengths. However, it would be somewhat inconvenient to measure angles in this way, so the International System of Units uses the Radian as an unit of plane angle. Radian is denoted by rad.

A radian (rad) is the measure of an angle subtended by two lines so that α = 1 rad, that is, for s = R,

as shown in figure 4.

Figura 4 - Definition of 1 radian.

The adoption of the name "radian" as a unit of plane angle is remarkably artificial, since it does not appear as most of the units derived from the International System, which are sets of other units related by operations. That's why the International System says the following:

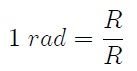
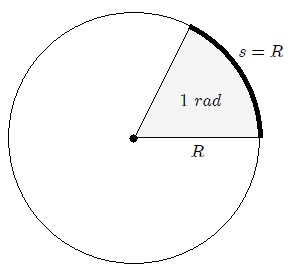
"Radian is a special name given to number 1, which can be used to provide information about the quantity it qualifies in. In practice, the rad symbol is used when convenient, but the symbol of the derivative unit 1 is often omitted when specifying values of dimensionless quantities ".

REFERENCES

Soldovieri, Terenzio & Viloria, Tony. EL ANGULO SOLIDO Y ALGUNAS DE SUS APLICACIONES. 1era edición (borrador). You can download it on my website http://www.cmc.org.ve/tsweb/
All the images presented here were elaborated by me. The color image constitutes the cover image of the text indicated above, of which i'm the author.
Real Academia Española. http://www.rae.es/ Diccionario de la Lengua Española. Electronic version that allows access to the content of the 22nd. edition and the amendments incorporated until 2012.
Faget, J. & Mazzaschi, J. TEMAS PROGRAMADOS DE FISICA - GENERALIDADES, volumen 1. Editorial Reverté, S.A., 1976.
Alvarez C., E. ELEMENTOS DE GEOMETRIA, CON NUMEROSOS EJERCICIOS Y GEOMETRIA
DEL COMPAS. Editorial Universidad de Medellín, 2003.

It is my wish that the present information can be very useful to all. Remember that the present is the first of a series of posts written with the final objective of presenting in a clear and simple way the definition of SOLID ANGLE. The next in this series will refer to the definition of the Diedro Angle, the Polyhedron Angle and to the intersection of a polyhedron angle with a sphere.
Sorry for my English!.
Until my next post. Regards! 😁