The Monk-Porridge Theorem

What has the above picture got to do with the following mathematical inequality problem?
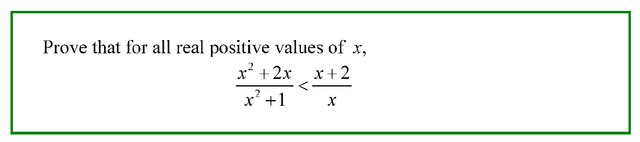
This inequality looks ... er ... challenging doesn’t it?
We do not know what x is, how can we conclude anything?
Think! Think! Think!
...
There is a Chinese idiom 僧多粥少 “many monks, little porridge” which describes a situation of shortage. In economics terms, the demand is more than the supply. Obviously, if a temple has some hot steeming porridge (or gruel) and there are more and more monks coming around, then there is less food to go around for each person. Some of them may go hungry. Maybe a few yet-unenlightened ones can get steaming mad and lose their self-eSTEEM. But if there are fewer monks, then each person can have a bigger share.
I formalise this common-sense observation into a mathematical theorem, which I call the Monk-Porridge Theorem.

In case you are wondering: what is a “theorem”? In the study of mathematics, a theorem is like a theory-gem. Something which you know for sure to be guaranteed, always true and reliable, and therefore very precious, like gemstones. Since I know it is always true, I can be confident in using it, and it will lead me to a valid logical deduction. OK, it is intuitively obvious. But, how do I know that it is indeed 100% guaranteed confirmed true? How do you know that it always works? We can have a formal proof as follows:-
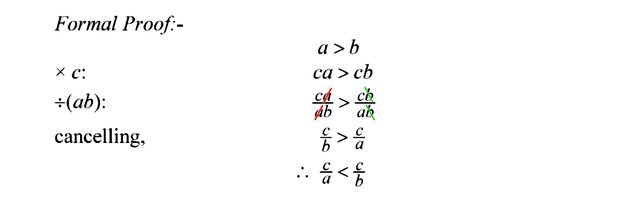
Assuming a to be greater than b, we can multiply on the left and on the right by c. Because c is a positive number, it does not change the direction of the inequality. Now ab (a times b) is also positive. So we can multiply through by ab, and the inequality still remains as ‘>’ and does not change to ‘<’. After cancelling, we get . Then we turn this around and say that
. Done!
Let us apply this to solve the inequality problem at the beginning.
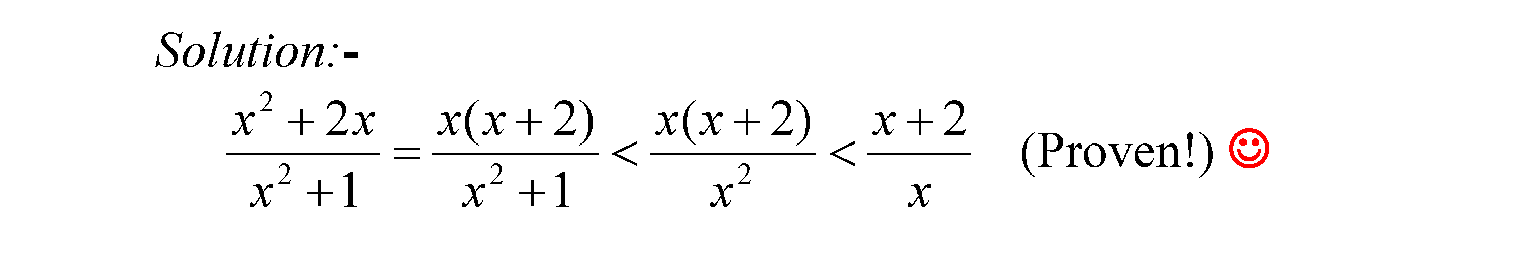
After factorising (“factoring” in Americanese) the numerator, we look at the denominator. If we changed the denominator from x²+1 to x², we are dividing by less, so we should get more. This is true regardless of the value of x, because x²+1 is always bigger than x². Notice now we can cancel away one pair of x’s. But that gives us which is what we want!
So today we learned the power of the Monk-Porridge Theorem and see how it can be applied to prove an algebraic inequality.
By the way, there is nothing special about porridge. I could have used pizza and called it the Hungry Children-Pizza Theorem, or perhaps the Cookie Monsters-Cookies Theorem. But you get the idea, yea?
@tradersharpe
-- promoting sharp minds
!originalworks
Announcements
Please join my mathematics contest. SBD to be given away!
Please read my post yesterday, which has a very important educational message, but it is under-appreciated, i feel.
Thank you everybody for reading my post and for your support!!!
@royrodgers has voted on behalf of @minnowpond. If you would like to recieve upvotes from minnowpond on all your posts, simply FOLLOW @minnowpond. To be Resteemed to 4k+ followers and upvoted heavier send 0.25SBD to @minnowpond with your posts url as the memo
My friend, a kind reminder here.
#cn tag is stand for Chinese.
However, no Chinese was detected in this article.
Please use wisely for your tag,thank you
僧多粥少 ;-)
@eileenbeach has voted on behalf of @minnowpond. If you would like to recieve upvotes from minnowpond on all your posts, simply FOLLOW @minnowpond. To be Resteemed to 4k+ followers and upvoted heavier send 0.25SBD to @minnowpond with your posts url as the memo