Auctions: Economic arbitrage

Imagine you are in Venezuela. Due to many economic changes over the past years, the purchasing power of your currency has gone down significantly against products, services and against other currencies. This to the point of hyperinflation, defined as >50% per month.
Recently the price of the black market VEF/USD reached parity with the gold currency in games like World of Warcraft, even going bellow that parity, as you can see in the Fortune article. Is almost natural that if you have access to the internet you would prefer to use such currencies - WOW gold, Cryptocurrencies- to transact despite being merely game currencies. In this sense, the internet becomes a vehicle to arbitrage.
What's Arbitrage?
Is a difference in price for the same or similar items due to market inefficiencies to make risk free profit. You ideally would buy in the market where the item is lower in price and sell on the market where the price is higher in price. It can be done in sequence or simultaneously.
There are two types.
- One is Pure Arbitrage, where the only limit is the current price difference and transportation/transaction fee.
- The other is Risk Arbitrage, where the price is speculative based on expectations of future events that might not actually occur.
Pure arbitrage is exceedingly difficult as time passes, due to computerized trading, where computerized systems already do this taking the retail investor out.
Of course, retail investors can take part in Risk arbitrage. Is a type of inside trading quite common in Cryptocurrencies, for instance. Buyers are following a project and a) gains early access b) buy before a big event c) buy after a bad news came out. All with the expectation of selling at a higher price.
There are reasons people prefer to sell (short) their "long-term investments" for a stronger currency when that currency is going up. One of them is fear, but even for more risky people it usually makes sense due to statistical arbitrage pairing. You have a model of how the world "should be" and take advantage of such imbalance.
Pairs Trading
Is a system that allows traders to benefit from any market condition. Pairs trading is based on stationarity. Stationarity is a stochastic concept, it means a series of points or moments through time, that have the same distribution parameters over time. If you suppose the distribution is normal (continuous), then the parameters are given by mean and standard deviation. You couldn't find a trend in the mean or in the standard deviation.
A part of point processes, we can use them regularly to model events that appear random or are governed by underlying causes like emotions.
You can think of most distributions as special cases in a binomial distribution (finite number of discrete random variables plotted that you can obtain through "binomial coefficients"), where the average=np and the variance=(np(1-p)). Where n is the number of events and p is the probability of such events.
An example:
During the times of the Prussian army, there were a lot of soldiers that were dying by being kicked by their own horses. It was such a problem that Ladislaus Bortkiewicz took measurements of the events and published a book on the Poisson distribution (discrete) of it[1].
The logic behind this is simple. If the events occur at random, like you would expect unless horses are part of a conspiracy, you will not find any pattern at all. Just pure randomness or stationarity (white noise).
The thing is we can't be sure something is noise just by assumptions or by the intuition of it. Graphs are got to quickly convey information about what isn't about what is. In fact, those horse attacks are closer to connected terrorist attacks. They are not completely independent of each other and the probability of one event following closely after the other increases with each attack. Like earthquakes that have after-shocks.
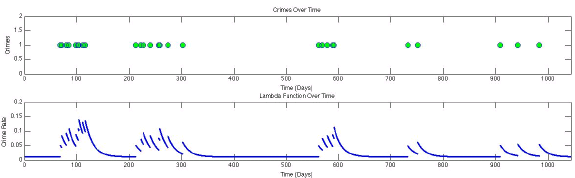
Example of Hakes process: Rival gang crimes plotted
To describe and predict such events the Hawkes process was developed. A mathematical description of how some events are not independent of one another.
Lambda(λͅ) represents the "intensity" of the event, this is the probability of an event to occur over a period of time. Mu(μ) is the background noise (randomness) of the event happening. Then every time (+) an event occurs (k0) the probability of that event increase but it doesn't last long, that duration dies quickly over time (g).
This equation shows the underlying processes going on hidden from us. e.g. If something pumps are probably some more things are gonna pump soon. If something dumps equally. The mobility then depends on how much can you arbitrage - this is how costly and difficult is the transition to other markets and other assets - your current position and how rational is the market (see Keynes Beauty Contest).
So the more inefficient the market and more irrational the more you benefit from arbitraging and finding the routes for it. Is probably the most important thing in commerce. It could be playing WOW, if your country is uber irrational and you have a fast arbitraging mechanism like internet access.
No trading zone
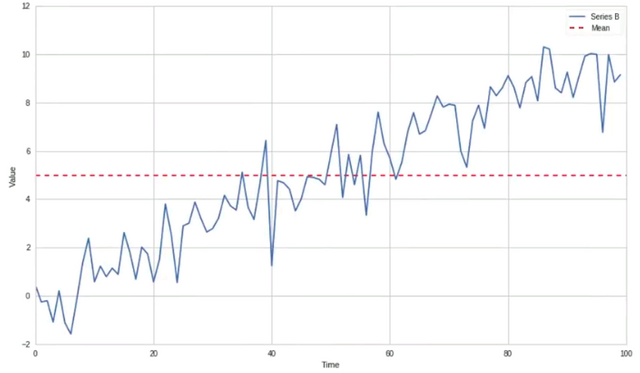
When the trend is non-stationary you can't find statistical information about the parameters, except at marginal moments like the red line depicted above. Trend zones like the one depicted above are places where traders and auctioneers can at least see the index of the market and can make a profit based on that trend.
This is what some call "trading fishes":
A fisherman caught fishes that he sold to a man in the market who in exchange gave him hard currency. This man in the market sold them to a distributor who in exchange gave him some transport services. The distributor gave some of the fishes to a farmer in exchange for fixing a fence. The farmer and his family ate the fishes and got sick. So the farmer didn't fix the fence and reclaimed to the distributor that the fishes made him sick. Since the distributor had lost that job he went to the man in the market to get retribution for his transport since the fishes made the farmer sick. The market man went to the fisherman to get back his hard currency. The fisherman denied the return of money by saying this: - I see what's your mistake. Those weren't eating fish, they were trading fishes.[2]

Trader's keep a product alive by following the impetus of a trend but when stationarity appears, they no longer know. - It's about to break so either it will go up or it will go down- they say. What they mean to say is that at that point, without a discernible trend, the process has become too complex for them to follow or act on.
What people can do is check for stationarity and find hidden features, that predict future trends. This is risk arbitraging into the next boom and ripples of that boom. Like a surfer that follows big waves. Is the essence of what some call "swing trading".
In order to check for stationarity one can apply the Dickey–Fuller test.
Which I'll explain next week applied to the auction of a real asset.
Not all irrationality is equal. If one assumes meritocracy while the market is irrational then wealth is being redistributed. The more friction there is the more of it is getting lost in the channels. Sometimes one needs to flee from irrationality, sometimes one needs to flee into irrationality. What is important is how that irrationality is redistributing wealth and go to the place where a part of the redistribution can go to you.



True talk, the most important thing is how irrationality is redistributing wealth, this is more important to everyone with the right passion to make wealth.
Good information write up, Tnx for sharing this great piece of information.
I wish you a wonderful STEEMMING in this year 2018.
WEALTHCOME to the world of WEALTH
That's great information
ha ha nc bro
Generic comments could be mistaken for spam.
Your Reputation Could be a Tasty Snack with the Wrong Comment!
Thank You! ⚜
Yeh really a very nice information....thank you for sharing with us....@stempede
its is Infomative And good for us Thank you dear for posting such post I follow you Happy new year
I am interested in your ideas and your insights, your post is very good and interesting, I had time to think like you in making post, your post is clearly accurate and clear meaning, I guided you from want to be the best like you, I am amazed to you, I am amazed dengab jepinteran you hopefully you continue to make and develop your logic and skill in making post, thank 😘
This post has received a 0.05 % upvote from @drotto thanks to: @steemstem-bot.
Well done! This post has received a 16.67 % upvote from @litasio thanks to: @steemstem-bot. Whoop!
If you would like to delegate to the @LitasIO you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP. Be sure to leave at least 50SP undelegated on your account.