Kill Time With Recreational Math - The Generalized Collatz Conjecture
I normally post every day but this one took me a few days to write the programs and to work out what the results meant. It was fun little mathematical journey in which I try to generalize the Collatz conjecture and fail (but that's life). I hope you enjoy the post.
The Collatz conjecture is a deceptively simple sequence:
- Start with any positive whole number, n > 1.
- If the number is odd then multiply it by 3 and add 1.
- If the number is even then divide it by 2.
- Use the result as a new number and apply the above rules again.
- Keep going until it ends up at one or it diverges.
The conjecture is that for any number n, the sequence will always end up at one. This is also called the 3n + 1 conjecture and it is apparently unprovable.
Paul Erdős (a scary smart mathematician) said about the Collatz conjecture: "Mathematics may not be ready for such problems." If Paul Erdős thinks it's a hard problem then, yep, it is likely a very hard problem.
In this post we will explore the Collatz conjecture 3n + 1 using a python program and then later check out its generalized form:
where for Collatz a = 3, b = 1, m = 2 and n is some number that you start the sequence at.
In the program below the there are three loops:
- an outer loop for the modulus 'm',
- an intermediate loop for the addition term 'b'
- an inner loop for the multiplier 'a'
- the term 'i' is just the whole number that starts off the sequence. It will iterate from 2 to 25000 to check out the first 25000 sequence starters to see if they collapse to 1
- the inner loop checks if the sequence has collapsed to 1 and prints out all the parameters when this happens
- the term 'maxcount' just tracks the maximum iteration of all the numbers checked so far.
- the inner loop has a fail safe, it bails out if the iteration number exceeds 10,000 (i.e. the conjecture is false and the sequence might be diverging). If the iteration count gets this high then I will assume failure, or just check that sequence in more detail later to see if it really was a failure in the conjecture.
import math
import time
import datetime
# **********************************************************************************
#
# This code released under CC BY-SA 4.0 license by Procrastilearner
#
# Collatz conjecture: n_i+1 = 3*n_i + 1 if odd, n_i+1 = n_i/2 if mod(n_i,2) == 0
# Reference: https://en.wikipedia.org/wiki/Collatz_conjecture
# Generalized Collatz conjecture: n_i+1 = an_i + b if odd, n_i+1 = n_i /m if mod(n_i,m) == 0
# a, b, m belong to the set of positive integers
#
# **********************************************************************************
DT = datetime.datetime.now()
print(DT)
a = 3 # multiplication term 'a'
b = 1 # addition term 'b'
m = 2 # modulus 'm'
print("a, b, m, starting number, #cycles to reach n = 1")
while(m <= 2):
while(b <= 1):
while(a <= 3):
i = 2
count = 0
while(i <= 25000 and count < 10001):
count = 0
num = i
while(num > 1 and count < 10000):
if(num % m) == 0:
num = num / m
if num == 1:
break
else:
num = a * num + b
count += 1
i += 1
print(str(a) + "," + str(b) + "," + str(m) + "," + str(i) + "," + str(count))
if count >= 10000:
break
a += 1
b += 1
a = 3
m += 1
a = 3
b = 1
DT = datetime.datetime.now()
print(DT)
The Results
The screenshots below show the output for at the start of the program run and the end of the run.
Starting number n from 3 to 21:
Starting number n from 24982 to 25001:
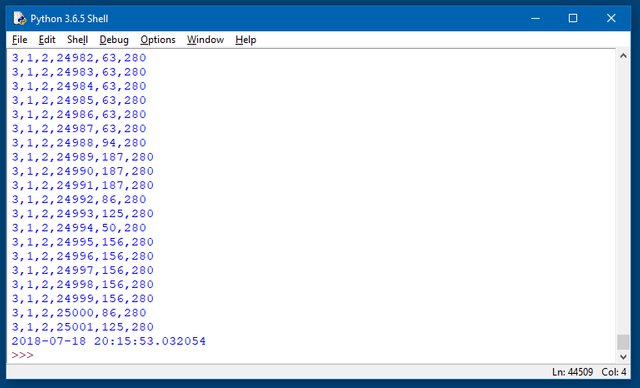
It looks like from the numbers 3 to 25,001 the maximum number of iterations in the sequence before it collapses to 1 is 280.
This is not proof that the Collatz conjecture is true, not by a long shot. It just gives you confidence that there is something there. As mentioned above, actually providing a proof might be something that is outside of the realm of current mathematical knowledge.
The Generalized Collatz Conjecture
The original Collatz conjecture is (3n + 1)mod 2 and it appears that the sequence always collapses to 1 no matter what whole number you start with.
We can make the sequence more general: (an + b)mod m where 'a' replaces the mulitplier '3', 'b' replaces the addition term '1' and 'm' replaces the modulus 2.
For fun we can ask, are there other combinations of a, b, and m that also always collapse to 1?
Let's modify the above program to find out.
The modifications made are to:
- increase the limits on the loop to search a larger number space.
- only check out values of a, b and m that are prime. An early attempt found that non-prime values of a, b and m produced uninteresting degenerate solutions (i.e. sequences collapsed to 1 only because a, b and m were not coprime).
- changed the print functions to create a markdown table.
# **********************************************************************************
# This code released under CC BY-SA 4.0 license by Procrastilearner
# **********************************************************************************
import math
import time
import datetime
import sys
import os
# Collatz conjecture: n_i+1 = 3n_i + 1 if odd, n_i /2 if mod(n_i,2) == 0
# https://en.wikipedia.org/wiki/Collatz_conjecture
# Generalized Collatz conjecture: n_i+1 = an_i + b if odd, n_i /m if mod(n_i,m) == 0
# a, b, m set of positive integers
# Check if number is a prime
def isprime(n):
#source of this function is from:
#https://www.daniweb.com/programming/software-development/code/216880/check-if-a-number-is-a-prime-number-python
#check if integer n is a prime
# make sure n is a positive integer
n = abs(int(n))
# 0 and 1 are not primes
if n < 2:
return False
# 2 is the only even prime number
if n == 2:
return True
# all other even numbers are not primes
if not n & 1:
return False
# range starts with 3 and only needs to go up the squareroot of n
# for all odd numbers
for x in range(3, int(n**0.5)+1, 2):
if n % x == 0:
return False
return True
DT = datetime.datetime.now()
print(DT)
a_start = 3
a = a_start
b_start = 1
b = b_start
m_start = 2
m = m_start
#print out the markdown table header
print("a|b|m")
print("---|---|---")
while(m <= 9999):
while(b <= 9999):
while(a <= 9999):
i = 2
count = 0
while(i <= 1000 and count < 10001):
count = 0
num = i
while(num > 1 and count < 10000):
if(num % m) == 0:
num = num / m
else:
num = a * num + b
count += 1
i += 1
if count >= 10000:
break
if count < 10000:
print(str(a) + "|" + str(b) + "|" + str(m))
#get next prime for a
while True:
a += 1
if isprime(a):
break
a = 3
while True:
b += 1
if isprime(b):
break
a = 3
b = 1
while True:
m += 1
if isprime(m):
break
f1.close
f2.close
DT = datetime.datetime.now()
print(DT)
The Result
The table below shows the output of the program after running it for about 14 hours. There appears to be a number of other combinations of a, b and m that also obey Collatz conjecture.
| a | b | m |
|---|---|---|
| 3 | 1 | 2 |
| 3 | 1307 | 2 |
| 3 | 1787 | 2 |
| 3 | 1987 | 2 |
| 3 | 2311 | 2 |
| 3 | 2609 | 2 |
| 3 | 3271 | 2 |
| 3 | 3499 | 2 |
| 3 | 3823 | 2 |
| 3 | 4159 | 2 |
| 3 | 4397 | 2 |
| 3 | 4519 | 2 |
| 3 | 5011 | 2 |
| 3 | 5333 | 2 |
| 3 | 5437 | 2 |
| 3 | 5477 | 2 |
| 3 | 5693 | 2 |
| 3 | 6089 | 2 |
| 3 | 6269 | 2 |
| 3 | 6917 | 2 |
| 3 | 7529 | 2 |
| 3 | 7621 | 2 |
| 3 | 9829 | 2 |
Verification
Let's use the first version of the program to check some of these sequences out to see if they hold up.
a = 3, b = 1307, m = 2: sequence diverges for starting n = 1308
a = 3, b = 1787, m = 2: sequence diverges for starting n = 1788
a = 3, b = 1987, m = 2: sequence diverges for starting n = 1988
... and so on and so forth.
So no, the deeper verification shows that it looks like the combinations found by the first program do not obey Collatz conjecture after all. The sequences diverge.
The second, modified program only checked the whole number starting sequence for the first 1000 starting numbers and so it missed the sequence failure at the higher numbers. Oh well.
This is why it is always good to double verify your program results to confirm that they are true.
Closing Words
Collatz conjecture, that the sequence generated by (3n + 1) mod 2 always collapses to 1, seems to be unique.
Making it general and checking the first several thousand combinations of a, b and m does not seem to produce any other sequences that always collapse to 1 for every starting n. They always seem to only produce diverging sequences.
This is an interesting mathematical conjecture and maybe in the future I will revise the above programs to be more robust, more automatic and to explore larger number spaces to see if there exists a companion sequence to the Collatz conjecture.
Thank you for reading my post.
Post Sources
[1] UNCRACKABLE? The Collatz Conjecture - Numberphile
[2] Collatz Conjecture - Wikipedia

This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
I did not know this conjecture, but I am really interessed reading how it works and the whole your description of the process.
Congratulations for your great abilities!
Hi, congratz, you are now listed on the Steemians directory (https://www.steemiandir.com/) You can read more about this initiative here: https://steemit.com/steemit/@anonyvoter/new-selections-of-july-19-2018 If you like this project it would be great if you could resteem the post to make more people aware of it.
If you don’t want to be listed just leave me a comment and I will delete your profile from the website. Thank you very much for reading and I’m looking forward to your feedback!
PS: I’m NOT a bot so… I’m really looking forward to your feedback 😊
Some time ago tried this with my gifted maths students; then got them to try 5n+1.... by hand :-) Found pockets of both convergence and divergence, and a cycle, but didn't thrash it out on a computer. It was just fun for them to see a bit of experimental mathematics.
You have received an upvote (from @rycharde) and a resteem (from @accelerator) as part of the new MAP Trail initiative to support curated content.
You can see your entry here and the curator who promoted your post.
All of this is free and part of MAP's mission to support quality content creators by supporting curators.
You may help support the MAP Trail by either upvoting, resteeming or delegating to @accelerator...
... or just upvoting this comment :-)
Hi @procrastilearner!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV