PLATONIC SOLIDS...... Universal Geometry......Tetrahedron..Hexahedron..Octahedron..Dodecahedron..Icosahedron!
The Universes Building Blocks. Tetrahedron-Hexahedron-Octahedron-Dodecahedron-Icosahedron
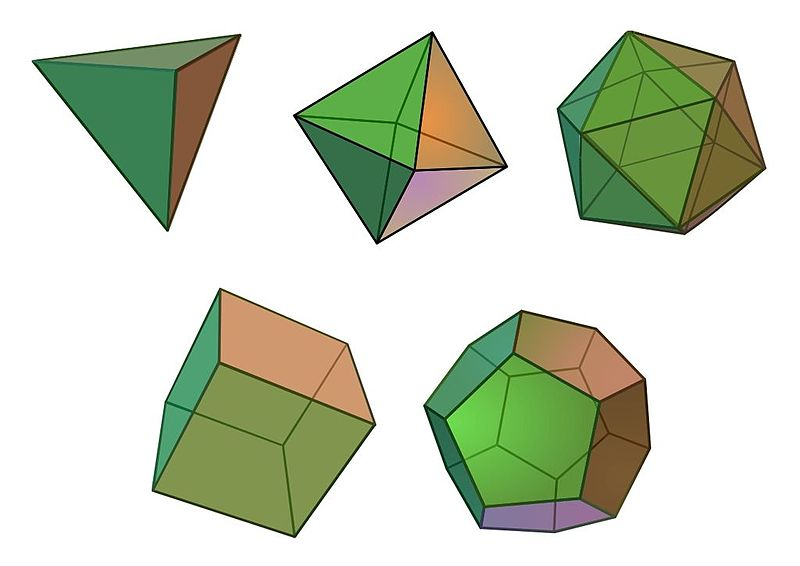
Image Credit:- wikimedia
The Platonic Solids
The Platonic solids are a special type of Polyhedrons (3-D shape), have been depicted throughout history dating back to the late neolithic period about 5200 BC, where representations of these shapes were carved into stone balls.

Image credit:- Wikimedia
They were studied by the ancient Greeks mostly famously, but the name given to them (Platonic) is misleading as they were believed to have been discovered by a friend of Plato called Theaetetus, who derived the mathematical representation.
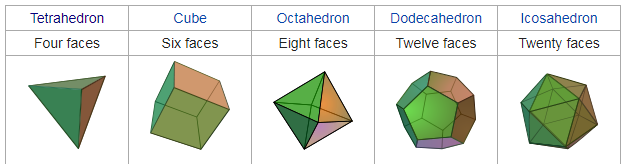
Image credit:- Extracted from Wikipedia
The name however comes from the fact that these shapes were described in the philosophy of Plato. He wrote about them in his dialogue Timaeus in 360 B.C, each of the solid were assigned an element of nature. The Hexahedron (cube) represents Earth, the Tetrahedron is fire, air is associated with the Octahedron, and water the Icosahedron. The Dodecahedron was described as "being used by God to arrange the constellations on the Heavens", and was also given the assigned the element of Aether (scientists dismiss this term, some may call it space-time) by Aristotle.
The famous Mathematician Euclid extensively described these solids mathematically. He stated that:-
For each solid Euclid finds the ratio of the diameter of the circumscribed sphere to the edge length.
This basically means that if you put a sphere around a platonic solid each corner of the solid will touch the surface of the sphere. Also you can nest all five of the platonic solids inside a sphere, all corners of each shape will touch the spheres surface and also touch the surface of every other solid.
Mathematical Properties
The Rules for being a platonic solid are:-
- All faces are convex regular polygons (symmetric 2-d shapes that are flat).
- No faces intersect.
- The same number of faces meet at each of its corners.
- Each vertex has the same interior angle.
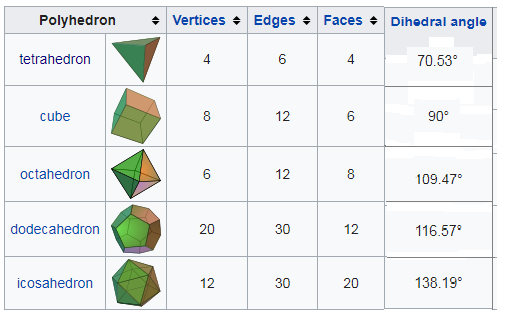
Image credit:- Extracted from Wikipedia
The angle associated with the vertices are called dihedral angles, it's the interior angle between two faces that's the same at every vertex. The equation used to determine the interior angle is
where p is number of edges of each face, and q the number of edges meeting at each vertex. This this equation and the information provided in the the table you will be able to confirm the dihedral angles.
Radii of Spheres contained in the Solids
Another interesting aspect of the Platonic solids is that they all have 3 characteristic concentric spheres.
- A circumscribed sphere which intersects all the vertices.
- A midsphere that's tangent to every edge, at the edge's midpoint.
- An inscribed sphere which is tangent to every face at the face center.
The are special radii associated with the spheres. The distance from the center of the polyhedron to the vertice is the circumradius. The distance from the center of the polyhedron to the edge midpoint is called midradius. The distance from the center of the polyhedron to the face center is referred to as the inradius.
The circumradius (R) and the inradius (r) of the solid (p,q), with an edge length (a) are expressed as
where theta is the dihedral angle I have mentioned. The midradius is expressed as
Values of these radii can be seen in the table below. Now I want you notice the constant phi, this is actually the Golden Ratio, derived from the the Fibonacci Sequence (0,1,1,2,3,5,8,13,21,....) that is seen all through nature. To obtain the golden ratio you must take divide a number in the Fibonacci sequence by it's preceding number, for example 21/13 = 1.61538461 . The value of Phi is 1.61803398, so you can notice a difference, the higher you go in the Fibonacci sequence the closer you will get to the true value of Phi when you divide the two numbers. I make this point because Phi is fundamental is nature, I can make a whole post just on that, but these solids contain aspects of the Golden ratio, very interesting indeed.
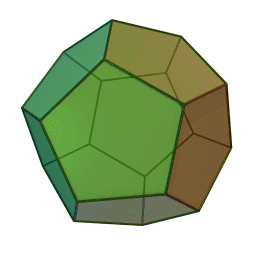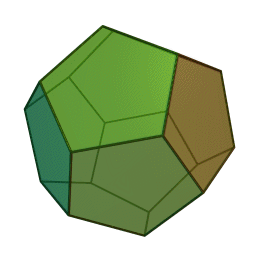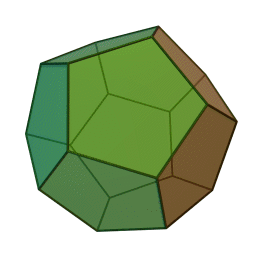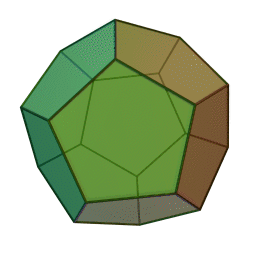
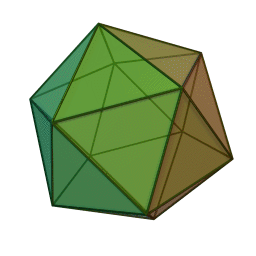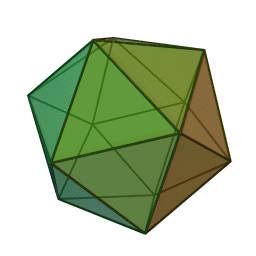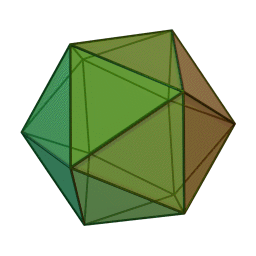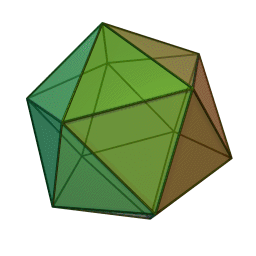
Below are nice GIF images of each Platonic Solid so you can have a good look at their geometry.
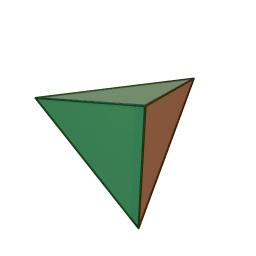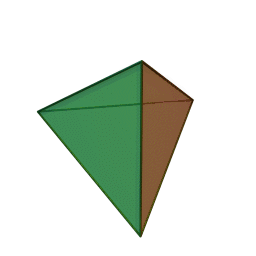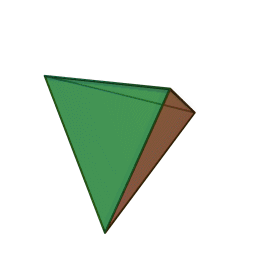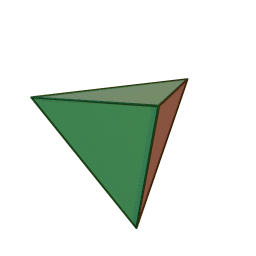
Tetrahedron
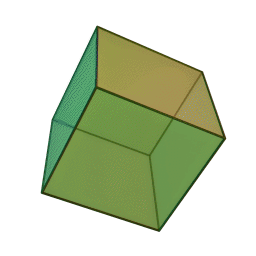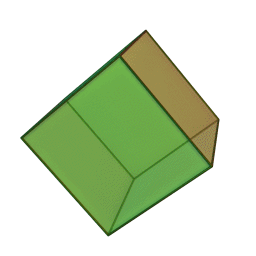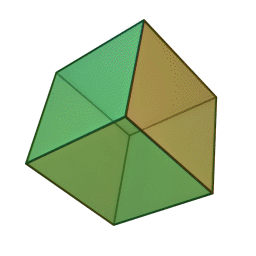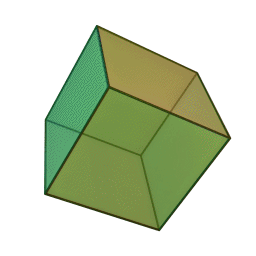
Hexahedron
Octahedron
Dodecahedron
Icosahedron
These GIFs were obtained from wikimedia, sourced in the platonic solid reference below.

Platonic Solids in Nature
Nature
The Dihedral angles of the tetrahedron, hexahedron and octahedron can be observed in naturally occurring crystal structure, their lattices have geometry that is platonic like.
On the larger scale of things I will point out that the Great Red Spot on Jupiter is located a position where a tetrahedron would touch the sphere, in the case that one vertex of the tetrahedron is located at the pole, then this is true. There are other example of this in the solar system, but it's not something that has been studied scientifically in depth, I just wanted to make that interesting point. For the open minded keep this fact in mind.

Image credit:- wikimedia
Biology
There is a type of protozoa called Radiolaria, it has been observed that skeletons of these exhibit platonic geometry, for example type was called Circogonia icosahedra, which you can see in the image below.
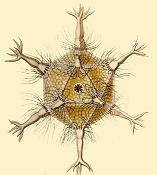
Image credit:- wikimedia
In fact many varieties of virus exhibit Iscoahedric geometry, herpes is an example, yeah it's gross i know. The structure of viruses are built from identical repeated sub-units of protein, and it just so happens that the icosahedron is the easiest shape to do this by conserving energy.
I discovered whilst writing this article that scientists have made DNA tetrahedron nano-structures for applications is biology, that's pretty cool. If you're interested check the paper HERE
One Dimension further..
I wasn't going to include this but I thought it was cool so i'll quickly introduce it. The platonic solids are 3-D right? Now take the principles and rules of them and apply it to 4-D. I can't even begin to imagine a 4-D shape so don't worry, but let's do our best. These shapes are referred to as Polytopes, you can read a bit further in the link at the bottom. It's completely impossible for our feeble human brain to imagine such a shape, but we can map out some representation. Below is a link to a short youtube video to help you visualise the 4th Dimension.

If you liked this post feel free to UPVOTE, FOLLOW, and RESTEEM.
References:-
Platonic Solids
Carved stone balls
Theaetetus
Great Red Spot
Polytopes
All images are Creative Commons or public domain, no copyright infringements have occurred.

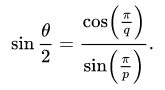
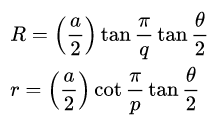
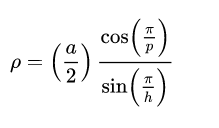



Being A SteemStem Member
Thank you @steemstem !
While i didn't understand much of what i read, because i'mnot so good at geometry, i did find this article interesting. and then the video on 4D. lol.. the shapes kept on messing with my mind. does 4D actually exist?
They mentioned that 3D space means you can pick any point in the space, and draw 3 axes out from that point, all of whom are perpendicular to the other 2. Easy enough to understand. But a 3D representation drawn on a 2D space (at 0:09 of the video) requires that some angles are mutated (the ones between red and yellow, for example). This is because in 2D space you cannot represent "the third axes perpendicular to the other two". However, our brains see that shape as 3D, probably because we live in a 3D world so our brain can "see" the 3 dimensional-ness of it.
Same goes for the 4D simulation. It is actually 4D, just that in a 3D space (2D, actually, since your computer screen is 2D) you can't draw all angles perpendicular to each other. Take 2:23 on the video, I think we can agree that green makes a cube, yellow too, one cube with the top shaded purple, one with the top shaded blue, one facing us with "yellow, red, green, red" vertices on top, and one at the back.
If a 2D square is made up of four 1D lines, and a 3D cube is made up of six 2D squares, what is a shape made up of six 3D cubes? 4D, of course, says my mathematical brain.
Awesome, simplified!
Yeah it's trippy the video I know. Just can't get my head around it either. 4-D exists but in a mathematical or abstract sense. We can never experience 4-D of space but we can work with it mathematically, string theory works in 11-D if i am not mistaken. 11-D? I don't want to abuse my brain, so i won't think too hard haha.
lol.. must be pretty awesome. who brought up this string theory? lol
The crazy physicist had to drop some heavy info in the conversation hahaha. Just say string theory and you seem like you know your stuff.
STRING THEORY :D
Awesome! simplified!
The Lego of Gods!
The Duplo of Zeus haha. Glad you liked it :)
Have some in my garden... this is the biggest.
Is this by any chance to try and harness energy? Like a pyramid?
Maybe known to members of secret societies, but I am an average person in the "common world" where many secrets still are unveiled world and we will have to discover them on our own...
I read something about the Pentagondodekaeder (German variation of the term) and got curious.
It is said that the knowledge about this fifth Plationic body was kept secret in old Greece. Pythagoras prohibited his students to speak a word about the Dodekaeder. Mind the correspondence with the classical four elements earth, water, fire and air.... but what was the fifth element?
I plan to write more about this topic and about my experiences in one of my next articles.
Yes, form obviously makes something with fields. The energy of this platonic figure is a smooth one, very calming and heart-opening.
Measurable physical effects... no idea but I hope to find out.
There are some amazing structures in nature that are dodecahedron shaped like the crystals of the shungite, a carbon-based mineral https://shungit-gifts.com/about-shungite
There are the fullerenes in general... https://en.wikipedia.org/wiki/Fullerene
like the Buckyball, the football with dodecahedrons and hexahedrons combined.
Also the mineral Pyrite forms dodecaeder structures. https://en.wikipedia.org/wiki/Pyrite
I need to apologize these are only some hints but it is not elaborated.
Maybe more, I'm too much in other projects at the moment but when I discovered your post I coujld not resist...
This I totally agree with, it's a reason i study physics, I want to know what is really happening with things and hopefully build a scientific thoery rather than speculative. This is what I hope anyway.
It' a problem I have also, so much I want to know and not enough time in one lifetime, let's hope we see some cool technology in the next 10 years that give us more time to live haha.
Have a wonderful day :D
when i see these geometric shapes i remember how much mathematics was helping me studying crystallography
Great job Mr @physics.benjamin thanks for sharing
Thanks for the comment. I find these shapes fascinating, and it's interesting how intrinsic such shapes are in nature. When seeing the mathematics and making sense of it you can see how perfect the whole concept is.
See you around ;)
hey, can you confirm somehow that the first image from that wordpress site is free to use for commercial use ? :)
It wasn't explicitly said on the source, so for safe measure I changed it. :)
Perfect thanks for that! Please when you have some time give this a read for future posts :p https://steemit.com/steemstem/@steemstem/guidelines-on-copyright-standards-in-steemstem
For sure dude. I've given it a good read, it was just that particular source, usually something is mentioned about copyright but nothing there. Thanks man ;)
No worries 😁😁