Introduction to Cryptography I: Encryption (Pt. 3 - Salsa20 Stream Cipher)
Hello there! @lemony-cricket here. Last week in Encryption Pt. 2, we learned what stream ciphers were. This time, we're going to take a closer look at a specific algorithm called Salsa20 in order to understand how the keystream is generated from the key.
Rocket graphic extracted from this CC0 image from OpenClipart-Vectors on Pixabay.
Retrospective
Unfortunately, participation was down last week. Thank you to @eonwarped for participating in the interactive activity! I'm not sure if the message was particularly malicious, but hey, Bob sure is really freakin' confused right now.
In an attempt to increase participation, this post will be the last in the series published on a Monday. From now on, I will be trying to post these on Friday or Saturday.
Also, it has come to my attention that my fancy lettering for newly-defined terms isn't showing up on some devices (particularly mobile phones with terrible Unicode support). That's unfortunate... so I'll be switching to bold italics, which are not nearly as fun. But enough about the series, let's talk about the crypto!
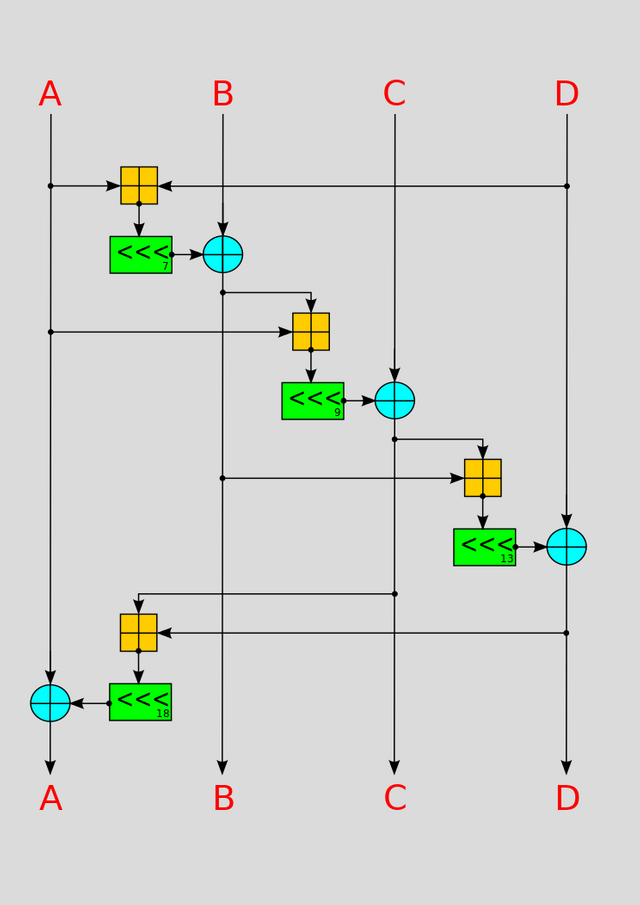
By Sissssou on Wikimedia Commons. CC BY-SA 3.0
The Salsa20 quarter-round
"rounds?" you mean like in boxing?At the heart of many cryptographic algorithms lies the concept of the roundd1. A round is like an algorithm within the algorithm; a sub-routine which is run many times to arrive at a final result. Salsa20's round function is actually itself made up of four quarter-rounds; the diagram to the right is a visualisation of the Salsa20 quarter-round function.
Huh? What are all those symbols? Well, there are three main operations in play. The orange crossed square represents addition modulod2 232. The blue crossed circle represents the bitwised3 exclusive-OR (XOR) operation (we learned the definition of XOR in the previous installment. Finally, the orange boxes with the <<< symbol inside indicate a leftward circular shiftd4 of the specified number of bits (either 7, 9, 13, or 18 as shown in the diagram, from top to bottom).
The lines represent input and output.. The quarter-round function operates on four 32-bit values at a time; A, B, C, and D. These inputs are taken from the cipher's current stated5.
Salsa20's internal state
hopefully, this will all start to make some sense soon.The quarter-rounds need data to operate on. That data is the current state of the cipher. For Salsa20, the state is a 4x4 grid of 32-bit values. Every time a quarter-round is executed, the existing data is overwritten with the newly generated output data. By now you're probably wondering... where is my key in all of this? We're about to find out.
expa | key0 | key1 | key2 |
| key3 | nd 3 | nonce0 | nonce1 |
| position0 | position1 | 2-by | key4 |
| key5 | key6 | key7 | te k |
To the left is a representation of the initial state of the ChaCha20 cipher. The subscript numbers indicate the N+1th 32 bits of that value. For example, "key0" indicates the first 32 bits of the key. The parameters used for the four quarter-rounds alternates from one round to another.
Specifically, there are two possible distributions of the quarter-rounds:
Odd
A | D | C | B
| | |
B | A | D | C
| | |
C | B | A | D
| | |
D | C | B | AFor odd-numbered rounds (including the first one, since the round numbering starts at 1), the four quarter-rounds each manipulate one of the state's columns.
Even
A B C D
- - - - -
D A B C
- - - - -
C D A B
- - - - -
B C D AFor even-numbered rounds, the above ordering is used instead, with the rows being manipulated rather than the columns.
Generating the keystream
tying it all togetherSalsa20's keystream is generated 512 bits at a time. These 512-bit segments are called blocks. In Salsa20, each block starts out as the initial state shown above, then 20 rounds are performed on that state. The initial state has three variable parameters: a 256-bit key, a 64-bit nonced6, and a 64-bit position counter (always starts at zero with the first block, and counts upward with each block).
After the initial state is built from the key and nonce, 20 rounds are run, one after another, on the state. At the end, what you have left in the state after those 20 rounds is 512 bits of your keystream.
Interactive exercise
You should have paper and something to write with for this portion.Let's run through a single round of a modified version of Salsa20. The rules of our modified version are as follows:
- All 32-bit values are 4-bit values instead
- Addition is modulo 24 instead of 232
- All circular shift operations are removed.
- All rounds are "odd-numbered."
The first person(s) to respond may use the following initial state. If you get here and someone else has already participated, you should use their output instead of this one, and reply directly to their comment. Let's have some fun with this!
1000 1101 1011 1011
0011 1110 0101 1001
0110 1010 0100 1111
0011 1101 1010 0100Make sure to ask questions if you get stuck! 🍋
Definitions
From my personal knowledge and experience unless otherwise noted.- round: a subroutine within a cryptographic algorithm which is repeated over and over, or a single iteration of this subroutine.
- modulo: the remainder after a division by the specified divisor. Used to create numerical systems that "wrap around." For example, 1 + 1 modulo 2 is 0.
- bitwise: describes an operation which operates on individual bits of a binary value.
- circular shift: a bitwise operation which shifts each bit in the specified direction, except for the last bit on that end, which is moved to the other side.
- state: a body of data which persists between rounds of a cryptographic function.
- nonce: a number meant to be used along with a key, but only once. The nonce should never be re-used with the same key again.
References
https://en.wikipedia.org/wiki/Salsa20
https://cr.yp.to/snuffle/salsafamily-20071225.pdf
Posted from my blog with SteemPress : https://lemony.cricket/2018/06/19/introduction-to-cryptography-i-encryption-salsa20-stream-cipher/
I wonder what the strengths and weaknesses of salsa20 are with respect to SHA256?
I looked up salsa20 and python, the sample code sure looks involved, maybe I will try to give that code a run one day.
Well, you might be quite figuratively comparing apples to oranges, but maybe not!
SHA256 is a hashing algorithm, and Salsa20 is a stream cipher. They are purpose-built for separate things. However, a stream cipher scheme could be constructed using SHA256; a quick Google search yielded this example.
So, what would the strengths and weaknesses of such a scheme be? Well, as one of the answers points out, only one keystream is generated by that algorithm. This is a weakness since it is actually really dangerous to re-use the same keystream to encrypt two different plaintexts.
This is easily remedied, though; just add a nonce. Instead of computing the keystream directly by hashing the shared secret, decide upon a random constant (doesn't matter what), concatenate it to the shared secret, and hash that to kick off your keystream. The nonce can be broadcasted in plaintext; it does not need to be private. After all of that is done, you should have a secure stream cipher.
So why use a purpose-built stream cipher like Salsa20 instead? Two reasons.
I think you got more of an answer than you were looking for, @procrastilearner, but I had fun writing it. Please don't hesitate to stick around for the rest of the series!
Also, nobody has done this post's activity yet; a 100% upvote awaits you if you do!
Wow. Great answer. Thanks.
Hi @lemony-cricket!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
bookmarked , will come back soon! Great write up btw!
Congratulations @lemony-cricket! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - Brazil vs Belgium
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes
Amazing stuff.
Posted using Partiko Android