Introduction to Navier Stokes Equation
You may have applied Newton's law of motion in solid particles. It is a fundamental and important formula in the classical solid mechanics. Have you ever wondered what would happen if you apply Newton’s law to fluids? Its simple, You will get Navier Stokes equation. This whole post is dedicated to this equation. It along with continuity equation is the basic governing equation in fluid mechanics.
The continuity equation is simply conservation of mass and Navier Stokes equation is simply momentum principle. In the equation, the three components of velocity and pressure are four unknowns. The momentum equation is vector equation so in 3 dimensions, it means 3 scalar equation. Along with continuity equation, the total equations we have is four. There are four equations and four unknown. Then, we can solve for the unknowns. The equation holds for all the control volumes in fluid domain. The solution means the pressure and three components of velocity in all the points of fluid domain. So, the Navier Stokes equations are field equations.
In principle, with four unknowns and four equation in NS equations, we can solve for unknowns. But in reality, it is very difficult to solve Navier Stokes equation. The exact solution exists for very simple cases. In fact, the existence and smoothness of general solution of the 3-dimensional Navier Stokes equation haven't been proven. The clay institute of mathematics has announced 1 million dollar prize for the proof.
Then, aren't we solving general 3 dimensional NS equation? of course not. Even I have solved NS equation. But, it is solved with a computer using numerical techniques. It is the approximate solution of NS equation. For the turbulence modelling, I have used RANS model where averaged NS equation is used.
The next section is the derivation of NS equations, you can skip this section.
Derivation:
For the derivation of continuity and NS equation, we should know Reynold’s transport theorem. I ain't going to derive this theorem in this article. It is simple to prove and you may refer to this video for the derivation.
According to Reynold’s transport theorem;
N = Extensive property, depends upon amount of fluid taken
m = mass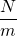
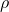
v = absolute velocity of fluid and it is a vector.
dV = Elemental volume of control volume
dA = Elemental surface area
CV = Control volume
sys = System
Using extensive property N as mass m; then n = m/m = 1
where,
The mass is conserved in the system so, the mass flow rate change of the system is zero. The rate of decrement of the mass in the control volume is equal to the mass outflux from the surface of the control volume. This makes sense.
Taking the differential under the integral sign using Leibniz rule.
To obtain the differential form, we should convert the surface integral into volume integral. This can be done using Gauss Divergence Theorem. This states that,
For the vector field F defined on the surface S and enclosing volume V is given by;
Using Gauss Divergence Theorem, the above equation becomes;
This must be true for any control volume CV so, integrant must be zero for the integral to be zero.
Finally, this equation is called continuity equation.
For incompressible fluid;
For the derivation of momentum equation i.e. NS equation, we should go back to Reynolds's transport theorem. Put linear momentum P = m v in place of N. Then, N/m is mv/m = v.
The LHS is simply, the rate of change of the momentum of system which is of course Force. Let me tell you that, the laws of physics apply to the system rather than the control volume.
The force on the control volume comprises of body force and surface force. The body force is force which acts on whole volume eg. gravitational force, electromagnetic force etc. The surface force acts on the surface example shear stress, pressure force etc.
So, the momentum equation changes to;
Now, taking the differentiation under integral and converting the surface integral into volume integral using Gauss divergence theorem;
This is actually called Cauchy equation. It has nine unknowns, i.e. three components of velocities and six components of stress tensor(among 9 components, 6 unknowns due to symmetry). But, the scalar equation is only three. So, we cannot solve this equation directly.
This may not look like vector equation as it contains divergence. But, the divergence is that of the tensor, which results in vector. So, this is a vector equation.
we know that;
Using this the Cauchy equation becomes;
From continuity equation, the term inside the bracket is identically zero. So,
This is alternative form of the Cauchy equation. But still, the unknowns are more that equations. We already figured out that the unknowns are in the stress tensor. The general stress tensor consists of normal stress i.e. pressure which acts normally and shear stress which acts along the plane.
So,
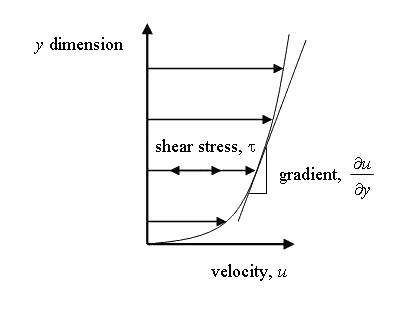
In solid mechanics, within the proportional limit, the stress is proportional to the strain. In case of the fluid, the fluid is continuously deformation so it is logical to relate shear stress with strain rate. If the shear stress is proportional to strain rate then such fluids are called Newtonian fluids.
strain rate = dv/dx
The viscous stress tensor is related to strain tensor for Newtonian fluid by the equation;
With the formulas and expressions above, the shear stresses can be expressed in terms of components of velocities. By doing so, the unknowns reduced to four and it is now equal to the number of equations. Putting the value in the alternative Cauchy equation,
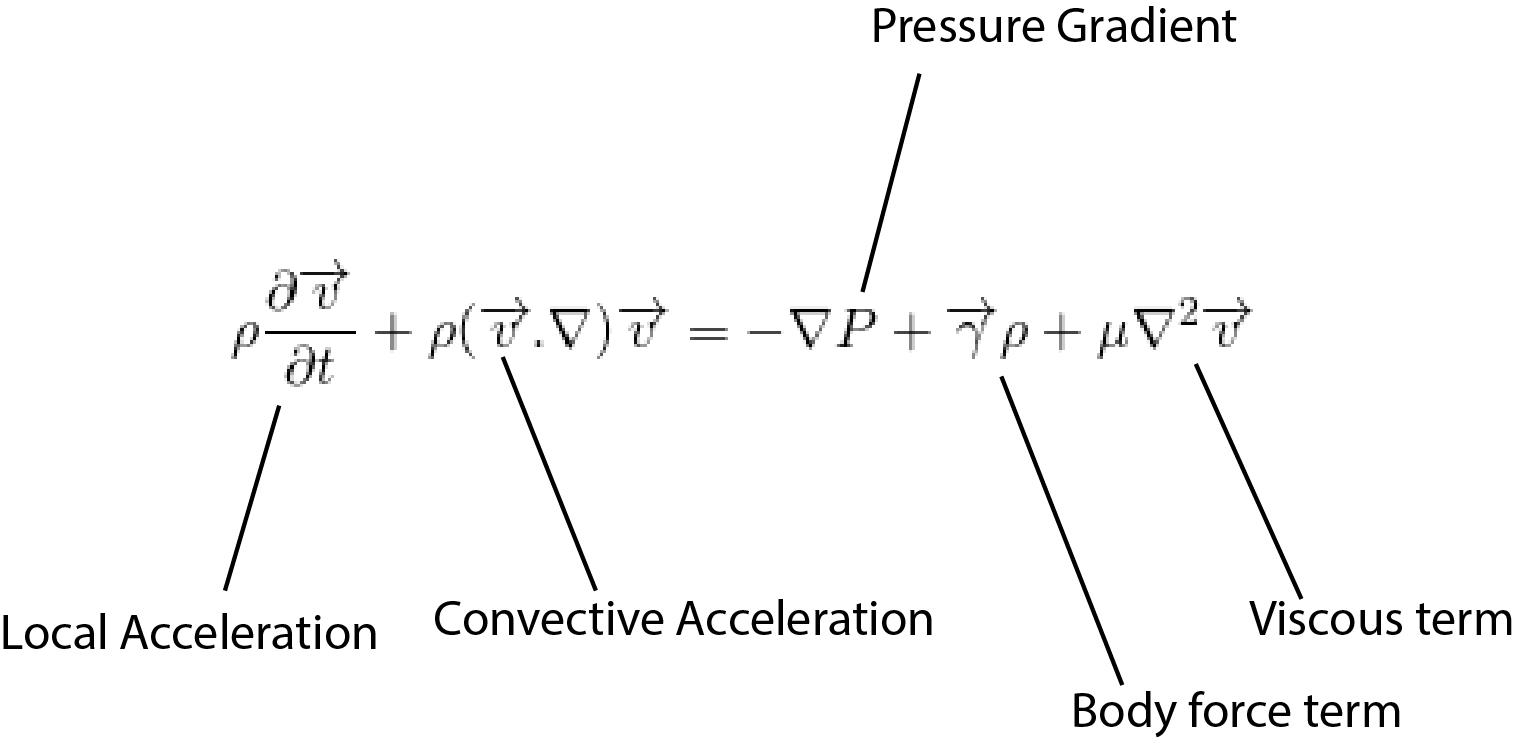
This equation is called Navier Stokes equation.
Breakdown
The above equation contains the terms like
local acceleration + convective acceleration = pressure gradient + body force term + viscous term
Density:
The density of the fluid is defined as the ratio of the mass of the fluid to the volume occupied by it. It measures the compactness of the fluid. Obviously, it has density less than that of solid. Generally, the liquid is assumed to be incompressible. That means the density of liquid remains same. The above NS equation is valid for incompressible fluids.
Acceleration
So, the total acceleration is the sum of local acceleration and the convective acceleration. The local acceleration is the acceleration of the fluid particles due to a unsteady flow. It is the change of velocity in different time. The fluid particles may be accelerated even in a steady flow. It can be due to change of position of the fluid particle. This is due to advecting or convecting to a new location. So, it is called advective or convective acceleration.
| Flow | local acceleration | convective acceleration | Example |
|---|---|---|---|
| steady and uniform flow | 0 | 0 | fluid flow at the constant rate through a uniform duct |
| Unsteady and uniform flow | non zero | 0 | fluid flow at varying rate through a uniform duct |
| Steady and non-uniform flow | 0 | non zero | fluid flow at the constant rate through varying diameter duct |
| Unsteady and non-uniform flow | non zero | non zero | fluid flow at varying rate through varying diameter duct |
Pressure Gradient
But, the pressure may vary in other directions too. So, to incorporate the changes in all direction, the gradient is used.
The pressure gradient is the measure of change in pressure as the fluid moves from one location to another. Pressure is simply the force applied perpendicularly on a unit area. So, when the pressure changes, the force also changes. Due to change in force, the fluid accelerates. It is the cause of fluid acceleration. It is also called pressure gradient force.
Body Force per unit mass
Generally, the body force acting in the fluid is gravitational force. The gravitational force per unit mass is g i.e. acceleration due to gravity. It acts vertically downward.
So, if only the gravitational force acts on fluid, then;
or,
where the y-axis is the vertical axis in the 3-dimensional coordinate system.
Viscous Term
When the solid object moves above the surface, the friction force acts to oppose the motion. Similarly, when the fluid moves, the layer attaching with the surface is assumed to be static. It is called no-slip condition. So, the layer touching the surface opposes the motion of upper layer and so on. This resistance to the fluid motion is called the viscosity of fluid. It shows the easeness of the flow of fluid. The water flows easily than honey because the honey is more viscous than the water.
It measures the viscous property of fluid. Higher the value of dynamic viscosity, the fluid is more viscous. Its SI unit is NS/m^s or Pa s.
| Fluid | Dynamic viscosity(Pa s) |
|---|---|
| Water | 0.00089 |
| Glycerine | 0.950 |
| Mercury | 0.0015 |
From the above table, it can be concluded that the Glycerine is most viscous among three fluids. Also, the flow rate of water is fastest for same shear stress applied as it has least dynamic viscosity.
References
Çengel, Y. A., & Cimbala, J. M. (2014). Fluid mechanics: fundamentals and applications. New York, NY: McGraw-Hill Education.
Young, H. D., Freedman, R. A., Ford, A. L., & Sears, F. W. (2004). Sears and Zemansky's university physics: With modern physics. San Francisco: Pearson Addison Wesley.
GRECKSCH, W., & SCHMALFUB, B. (1996). NAVIER-STOKES EQUATION. Computation and Applied Mathematics, 15(3), 227-239.
Constantin, P., & Foias, C. (1988). Navier-stokes equations. University of Chicago Press.
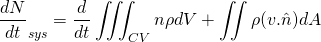
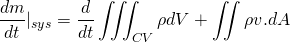
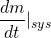
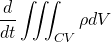
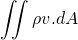
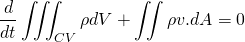
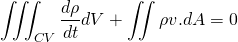
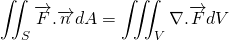
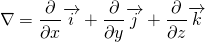
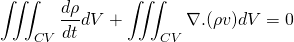
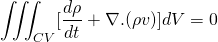
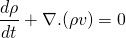
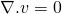
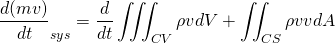
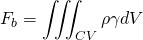
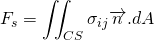
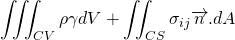
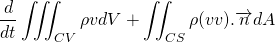
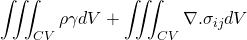
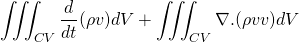
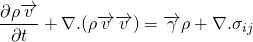
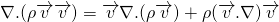
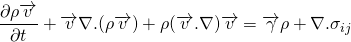
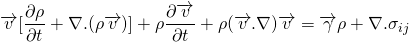
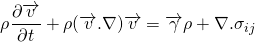
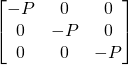
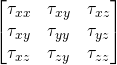
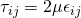
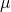
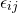
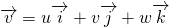
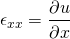
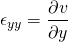
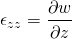
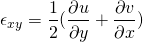
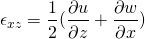
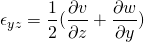
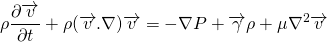
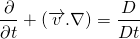
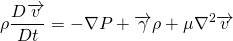
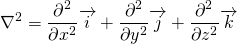
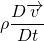
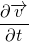
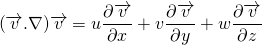
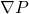

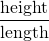
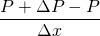
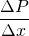
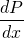
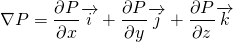
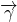
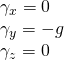
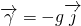
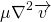
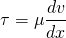
EventUp Secures $1.8 Million Investment from Groupon Founders, Expands to Chicago
In a significant move for the event planning industry, EventUp has successfully raised $1.8 million in funding from the founders of Groupon. This investment marks a pivotal moment for the company as it sets its sights on expanding its services to Chicago, a vibrant market known for its diverse event landscape.
EventUp, a platform designed to simplify the process of finding and booking event spaces, aims to leverage this new capital to enhance its offerings and reach a broader audience. The expansion into Chicago is expected to provide local businesses and event planners with access to a wide range of venues, making it easier to host everything from corporate gatherings to social celebrations.
The backing from Groupon's founders not only provides financial support but also brings valuable expertise in scaling a tech-driven business. As EventUp continues to grow, it is poised to become a key player in the event planning sector, offering innovative solutions that cater to the needs of its users.
For more details on this exciting development, you can read the full article by Ken Yeung on bub.blicio.us here.
👍✌
Thank you !!
Wow, very restless effort to analyse the Babies Stokes equations in so much detail. I had a Fluid Mechanics test in my 3rd year in the university where the only answer I got right were the babies Stokes equations in the three dimensions. Keep steeming
thank you
*Navier
Congratulations @bikkichhantyal! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPI studied fluid mechanics while studying civil engineering in my school days. I do not remember looking at the equation you provided. I remember it was so hard that it was hard. Thank you for giving me the opportunity to look through the memories. Thank you for choosing me as a friend. Let 's be good friends with each other. lucky7777
@bikkichhantyal you were flagged by a worthless gang of trolls, so, I gave you an upvote to counteract it! Enjoy!!
Congratulations @bikkichhantyal! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @bikkichhantyal! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Congratulations @bikkichhantyal! You received a personal award!
Click here to view your Board
Do not miss the last post from @steemitboard:
Congratulations @bikkichhantyal! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!