Card Trick and Mathematics: Theoretical Mission to the Moon
Hey Steemians. I’m going to mix two things that are highly unlikely. Card tricks and Mathematics! I know right? David Blaine and Gauss together. Well, that would mean that David Blaine can travel in time. Well, you know what I’m getting into.
We have often heard of hip-hop artists claiming they’d stack their cash high. So, high it would reach the moon (spoiler alert). Well, today we are going to put that to the test. But not in a conventional way. In fact, we are going to see how high you would get with cards instead of marijuana. “But Bikki, Gambling Is bad?”, well, so is smoking too much IYKWIM ;) And yet we do both. Perhaps next time we can use joints instead of cards. I’ll note that in my list of ideas. But for now, let’s stick to the cards.

The explanation is based on book prime obsession by Derbyshire(Ref 1). Without further delay, let’s start with the trick. Take an ordinary deck of cards. Put those cards on the table as shown in the figure above. Slowly push the topmost card of the deck. Push it until it just tips and falls. How far can you slide in without fall? (no pun intended) Since I have experimented I will give the answer.
It’s half of the card.
I can tell you it’s the truth since I never lie. But If you don’t believe me, you can see the second picture. The length of the card is 8.6 cm and I have marked 4.3 cm in the second from top card. If you push further, it falls. The halfway is the center of gravity of the card.

Now with the topmost card over hanged, let’s go to the second card from the top. Slide it slowly, until it tips and falls. How much overhang will you get? The tipping point will be center of gravity of top two cards. What’s the trick to find the center of gravity? Measure the common part and divide that by two, you will get center of gravity.
The common part of top two cards is
of the card. So, the center of gravity is at half of this value i.e.
from the tip of the second card. Remember that the half part of the topmost card is still there!!

So, total overhung part = 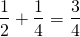
We already got  of the card hanging.
of the card hanging.
Further, let's go to the third from top card keeping above cards as they were. Now push it little by little. You will find that it can slide up to  of its part.
of its part.

Total overhung part = 
It's about 91% of the card. So, the question arises, can we overhang more than one card? Absolutely, if you push the fourth card, you can find that it can slide up to 1/8th of its length.
Total overhung part =
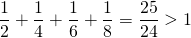
We can already see the pattern of the part that slides without falling.
For the
card from top, it is
of card
So, if we do the same with all 52 cards,
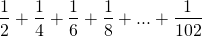
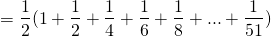
The end is on 51 cards because I chose the last card as the base from where, above cards overhang.
There is no any formula to calculate this sum directly. I somehow manually entered all the numbers and got the value as 2.25940659073334. This shows that we are able to overhang more than 2 and quarter of cards length. You can skip this manual work with a simple mathematical concept and with use of a mathematical tool in which computer enter all these values manually. Trust me!! the computer also doesn’t have a formula for this.
You can see that the sum is the value 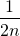 and n goes from 1 to 52 in above case. Mathematicians put a fancy sign to denote sum as below:
and n goes from 1 to 52 in above case. Mathematicians put a fancy sign to denote sum as below:
sum = 
Now using Wolfram Mathematica to calculate its value.
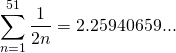
Its the same value I calculated manually earlier.
The obvious question is, how much can we increase this value? For that, I will use three decks of card lying around the house (Usually to play special card game played in South Asia named “Marriage”. Not as horrible as it sounds since we play with cards instead of people’s emotions). That won’t help much because it is really tedious work to overhang every card in (52*3 = 156 cards). Also, we have learned to use mathematical tool to calculate the value. Using the knowledge;
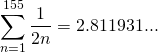
The value of the overhung part is increasing. But, we can see that it's increasing very slowly. As we have a mathematical tool now, let us consider that we have a large supply of card. Let us check the value of cards that can be over hanged if we use:
For the billion cards;
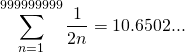
For the trillion of cards.

This is very interesting that you can overhang more than 14 cards. But, we are only concentrating on the overhung part of the card. Now, I will turn your concentration to the height of deck of card for above arrangement.
How to calculate the height of 1 trillion cards? Well, I still have a lot more tricks up my sleeves. I will assume that all the cards are identical and hence are of equal thickness. I measured the height of 50 cards and I got 1.7 cm.
Using simple unitary method;
Height of 50 cards = 1.7 cm
Height of 1 card = 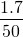 = 0.034 cm
= 0.034 cm
Height of 1 trillion cards = 0.034 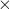 1000000000000= 34000000000 cm = 340,000,000 meters.
1000000000000= 34000000000 cm = 340,000,000 meters.
=  m
m
The height of moon from earth is 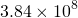 m. So, the height of deck of card for trillion of cards will be close to the moon. Just imagine: p
m. So, the height of deck of card for trillion of cards will be close to the moon. Just imagine: p
Since the number of cards that can be overhung is increasing but very very slowly. It is intuitive that there may be a certain limit of cards that can be overhung. But, that is not the case. There is no limit on that number of cards.
Give me an infinite supply of cards, I can overhang any number of cards.
@bikkichhantyal
That means I can overhang thousand, billion cards, trillion cards, 234563468236457826578465782346578623489523465879234653249875723486587234657823465872346578234658723645872346523465782634785634 cards, 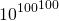 cards, google plex number of card if there are an infinite number of card supply. It is just a very large number okay?
cards, google plex number of card if there are an infinite number of card supply. It is just a very large number okay?
The Nerd Part
The observation and statement above are associated with a concept in mathematics. The main thing of interest is;
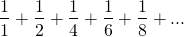
It comes in parenthesis for all case i.e. different values of n. Here, 1,2,3… ,n are the natural numbers. So, the series is the sum of reciprocals of the natural numbers. This is called harmonic series. The name harmonic is actually derived from music. The wavelength at nth harmonics is 1/n times of fundamental wavelength. I won’t explain this in detail. Refer to this site for more information.
I claimed that I can overhang any number of cards. I claimed that statement on the basis of a mathematical concept. The sum of harmonic series does not converge to a finite value. That means we can increase its sum by increasing number of terms in the series as we please. Mathematicians call these types of series divergent series. How did I know this is divergent series or its sum doesn’t converge? This can actually be proven by using various methods. I will explain two of them in detail.
Limit Comparison Method
The harmonic series is as follows;

In this series,
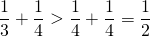
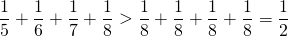

Since the sum is for infinite terms, there are any numbers of terms available for the sum.
Let’s take obvious divergent series;
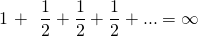
All the terms of the harmonic series can be so arranged that they are always greater than the corresponding term of above series. The above series is divergent imply that the harmonic series must be divergent.
Integral test
If you are familiar with calculus, then the integral test can be a very easy method to prove that harmonic series is divergent series.
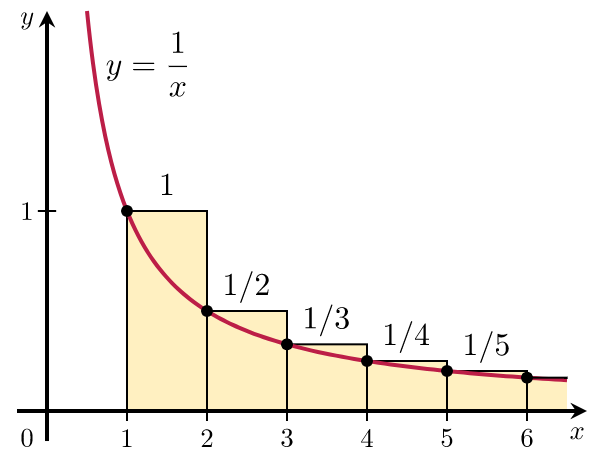.png)
(Source: wikipedia, Creative Commons' Public Domain )
The sum is a discrete sum. From the figure, it is shown that the continuous sum is less than the discrete sum. To find the continuous sum, using integration;
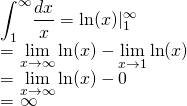
The continuous sum is 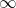 then the discrete sum which is greater than continuous sum must be
then the discrete sum which is greater than continuous sum must be 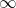 . And hence, the series is divergent.
. And hence, the series is divergent.
References:
Derbyshire, J. (2003). Prime Obsession. In J. Derbyshire, Prime Obsession. Joseph Henry Press.
Hardy, G. H. (2000). Divergent series (Vol. 334). American Mathematical Society
Dunham, W. (1990). Journey Through Genius: The great theorems of mathematics. Wiley.
http://tutorial.math.lamar.edu/Classes/CalcII/Series_Special.aspx
https://www.earmaster.com/music-theory-online/ch04/chapter-4-6.html
Reference mathematical tools
www.quicklatex.com
steemstem:
SteemSTEM is a community driven project which seeks to promote well-written and informative Science, Technology, Engineering and Mathematics posts on Steemit. The project involves curating STEM-related posts through upvoting, resteeming, offering constructive feedback, supporting scientific contests, and other related activities.
DISCORD: https://discord.gg/j29kgjS
follow me @:


Being A SteemStem Member
I am sorry but Wolfram-alpha is for non-commercial use only. http://www.wolframalpha.com/termsofuse/
But you can reference the Wolfram page about this problem http://mathworld.wolfram.com/BookStackingProblem.html
Apparently, Wolfram also has an overhanging cards demonstration project http://demonstrations.wolfram.com/OverhangingCards/
Thank you so much for the comment. I edited my post and referenced wolfram. Actually, I didn't use Wolfram for the content, I only used it for the calculation. Anyway, the demonstration looks cool!! Thank you again.
That is fine. But you cannot use the screenshots from wolfram alpha since your steemit post has commercial value.
I think everything is fine now.
Your sum operators are missing parameters in their subscript. Correct sum notation is
Corrected that too. Feel free to comment if there are any other mistakes/typos.
yeah totally
I actually just watched something similar on #startalk
super nerdy talkshow with #NeilDegrasseTyson
Apparently If you follow piece of paper in half 42 times it will also reach the moon :)
#nerd
#astrophysics
#moon
@bikkichhantyal cheers :)
Oh! that is too, interesting.
cheers :D
You wrote 25/25 instead of 25/24 in one of t he equations. Probably a typo :)
Yeah it was. Corrected it. Thank you so much.
I have to admit that (besides obvious math knowledge) you have a great sense of humor. Keep writing stuff like this on your blog – I am sure you will attract many readers and followers. Good luck with your studies and career!
And if you measure how many blunts is needed to reach the Moon – share it with the community :-)
Thank you so much. Obviously, with this much love, it would be difficult for me not to write. Thank you for your wishes and I hope to be a better presenter with every next article.
It's great to see mathematics implemented on such great magic.But it will be quite costly to buy so many cards
Actually, that is the magic of mathematics. We can predict things without experimenting. You dont have to go to center of earth to determine g is 0 there ;p
I was just checking the Prime Obsession book. If I am correct the first section of this post is a re-telling of Chapter 1 Card trick. Maybe you should already explain this in the beginning. If you give a reference you should refer to it in the text otherwise it is not a reference but a source for further reading.
I didn't know about reference and source thing. I'll consider your suggestions.
no problem. There is still time to make adjustments.
I already made.
Nice!