Saludos queridos lectores, bienvenidos nuevamente a mi Blog. En está oportunidad les hablaré un poco acerca de Series de Fourier y algunos ejemplos en GNU Octave, en esta oportunidad motivaremos el tema con un poco de historia luego mostraremos la teoría envuelta, y pasaremos a mostrar algunas aplicaciones y como usar el entorno GNU Octave. La misma está dirigida al público en general (aunque debemos acotar, este es un tema de un nivel más alto, para el que es necesario tener de algunos conocimientos previos de análisis real, cálculo avanzado, entre otros más), con atención especial a profesionales y estudiantes universitarios en ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

Introducción Histórica

La idea básica de la serie de Fourier es que cualquier función periódica f de, por ejemplo, el tiempo se puede expresar como una suma trigonométrica de las funciones senos y cosenos con el mismo período T

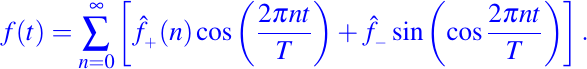
La idea nació de forma natural en el estudio de problemas de astronomía. Neugebauer (1952) descubrió que los babilonios usaban un tipo primitivo de Series de Fourier para la predicción de eventos celestes.

Más recientemente D'Alembert (1747) y su discusión sobre las oscilaciones de las cuerdas de un violín. El desplazamiento u = u(t, x) de la cuerda, como una función del tiempo t mayor o igual a cero y la posición x, es una solución de la ecuación diferencial parcial

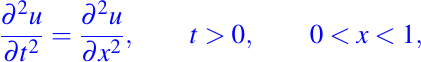
sujeto a las condiciones


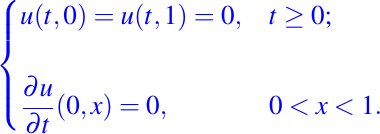
La primera condición expresa el hecho de que los extremos de la cuerda [x = 0, 1] están atadas; la segunda y última condición expresa que la cuerda está en reposo en el momento t = 0.

La solución de este problema es la superposición de dos ondas que viajan en direcciones opuestas a la velocidad 1, como lo expresa la fórmula de D'Alembert:

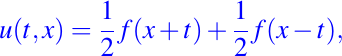
en la cual f tiene que ser una función impar del período 2, anulándose en x = 0, ± 1, + 2, ..., para hacer u se anule en los extremos de la cuerda. Posteriormente Euler (1748) propuso que tal función podría expandirse en una serie de la función seno cuyo período sea 2


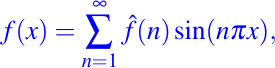
con lo cual resulta que


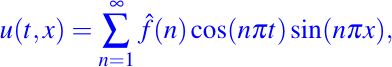
El armónico simple que aparece en la función anterior, es decir,


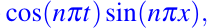
es interpretado como un modo fundamental de la cuerda y la frecuencia n/2 como en uno de sus tonos fundamentales. La misma idea fue propuesta por Bernouille (1753) y Lagrange (1759) con bastantes críticas de ambas partes. La fórmula


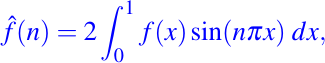
para calcular los coeficientes, más tarde asociada con el nombre de Fourier, aparece por primera vez en un artículo de Euler (1777).

Las contribuciones de Fourier empiezan en el año 1807 con sus estudios sobre el problema de flujo de calor

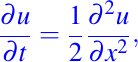
presentado a la Academia de Ciencias en 1811 y publicado como el famoso Théorie analytique de la chaleur (1822). En este, realizo un intento muy serio de demostrar que cualquier función suave a trozos f puede expresarse como una suma trigonométrica. Una prueba de este hecho fue encontrada posteriormente por Wardich (1829). Riemann (1867) también dio importantes aportes a este problema.

---

---

Introducción

Comencemos con una definición formal de una función periódica:

Definición 1

Una función f(x) en una variable x es llamada periódica, con periodo T > 0 si el dominio de f contiene a x + T siempre que contenga a x y si para cada x en el domino de f tenemos

También podemos observar que si x - T pertenece al dominio de f, entonces f(x - T) = f(x). Por lo tanto, se deduce que si T es el período de f, entonces mT también es un período para cada número entero m > 0. Adicionalmente, el valor de T positivo más pequeño para el cual (1) se satisface se le llama período fundamental de f.

Por ejemplo, las funciones

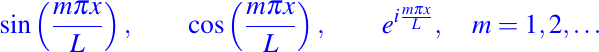
son funciones periódicas con periodo fundamental T = (2m)/L. Notemos que también tiene un periodo común 2L.
A continuación mostramos un las gráficas para la función coseno antes descrita, para el valor de L = 2 y valor de m = 1:4.


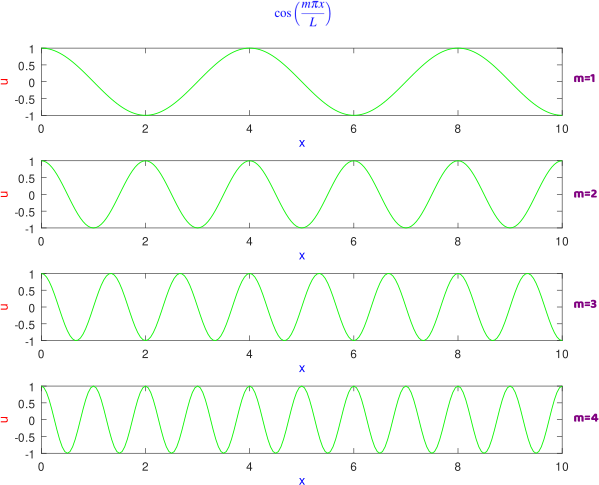
_{Gráficas de una función periódica. Elaborada con GNU Octave, por @abdulmath.}

Adicionalmente les dejo el script, para que puedan jugar un rato, con el:

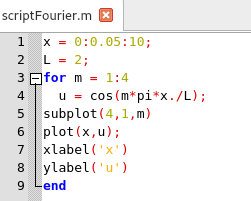
_{Script para gráficar las funciones periódicas. Elaborada con GNU Octave, por @abdulmath.}

Si alguna función f se define en el intervalo [s, s + T], con T > 0 y f(s) = f(s + T), entonces f puede extenderse periódicamente con el período T a toda la línea como

Por lo tanto, podemos suponer a partir de ahora que cada función periódica se define en toda la recta real.

Definición 2

Supongamos que el dominio de f es simétrico con respecto al 0, es decir, si x pertenece al dominio de f, entonces - x pertenece también al dominio de f. A un función f es llamada par si


o impar si

Polinomio Trigonométrico

Un polinomio trigonométrico es una función P del conjunto de los números reales en el mismo, la cual podemos expresar de siguiente manera:

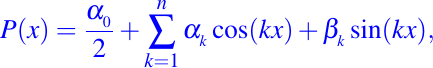
donde

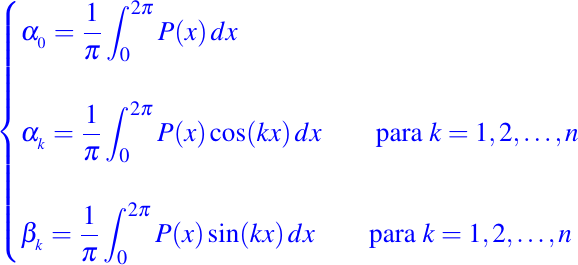
Coeficientes de Fourier

Sea f un función definida del conjunto de los números reales en el mismo, cuyo periodo es 2pi, y que además es integrable en el intervalo [0, 2pi], entonces los coeficientes de la serie de Fourier de f están dados por

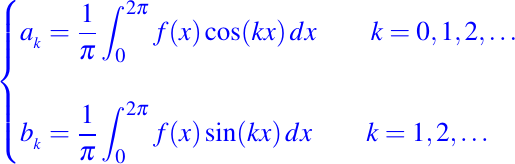
La serie de Fourier de f la podemos entonces expresar como la suma formal infinita siguiente

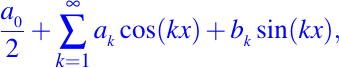
A continuación presentaremos dos ejemplos en donde podremos observar como se comporta la serie de Fourier de la función f. Es de hacer notar que la la convergencia está garantizada en todos los puntos de continuidad de la función.

---

---

Ejemplo 1

Sea la función siguiente definida por

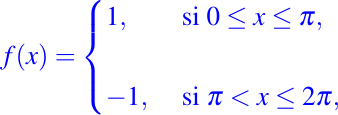
como hemos visto ya anteriormente, esta función la podemos extender a toda la recta real a través de la periodicidad. Es muy fácil verificar por simple integración que la serie de Fourier de la función f la podemos expresar de la siguiente manera

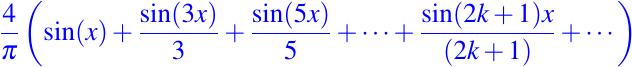
Sea las sumas parciales hasta n = 5 de la serie de Fourier de f dada anteriormente, definida como

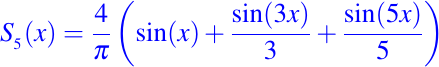
A manera de tener una mejor perspectiva de el comportamiento de la serie de Fourier de f, las gráficas dadas a continuación, de cada uno de los factores del desarrollo de las sumas parciales de S₅, las podemos visualizar por separado como sigue:


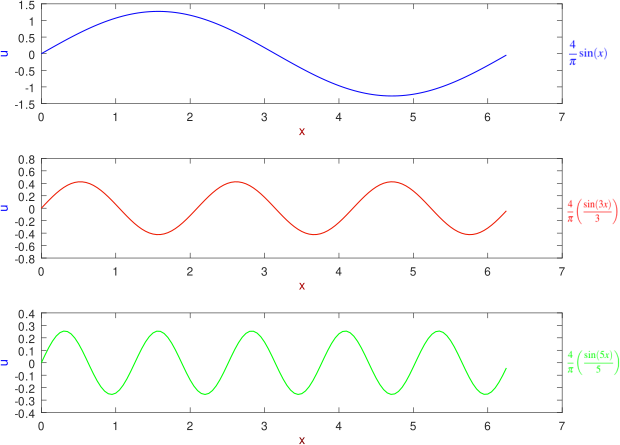
_{Gráficas de las funciones del desarrollo de la serie Fourier. Elaborado con GNU Octave, por @abdulmath.}
Luego, si tomamos la suma parcial, es decir, sumamos todos los factores anteriores, tenemos el gráfico de S₅, dado por:


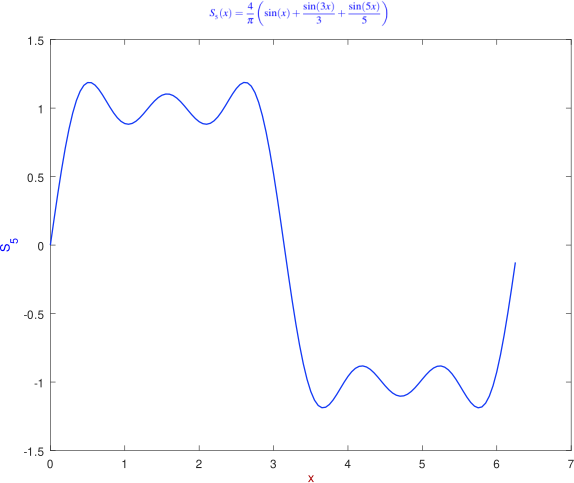
_{Gráficas de las sumas parciales del desarrollo de la serie Fourier. Elaborado con GNU Octave, por @abdulmath.}
Si ampliamos las sumas parciales, y ahora tomamos las sumas parciales S₁₁ y S₁₅ cuyas ecuaciones vienen dadas por:





entonces, podemos comparar el comportamiento de estas con respecto a la función f como vemos en el gráfico anexo


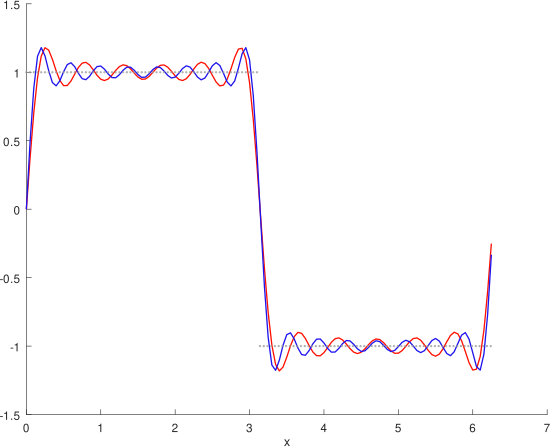
_{Gráficas de S11 en rojo y S15 en azul, de la serie Fourier y la función f. Elaborado con GNU Octave, por @abdulmath.}

---

---

Ejemplo 2

Dada la función f definida por

la cual podemos extender por periodicidad a toda la recta real, como ya lo dijimos en el ejemplo anterior, y como lo mostramos en la definición. De esta manera, podemos calcular la serie de Fourier de la función de manera muy fácil, solamente resolviendo las integrales de los coeficientes, usando integración por partes, integración trigonométrica e inmediata, obteniendo de esta forma la siguiente expresión:


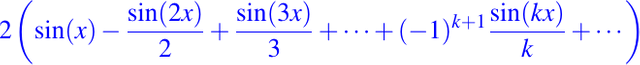
Tomemos la suma parcial S₃(x) de la serie de Fourier dada en la ecuación anterior, la cual viene expresada por:


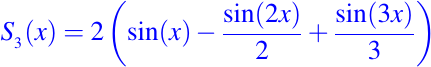
A continuación mostraremos las gráficas por separados de cada una de las funciones envueltas en la suma parcial S₃(x) de la serie de Fourier de f como sigue:


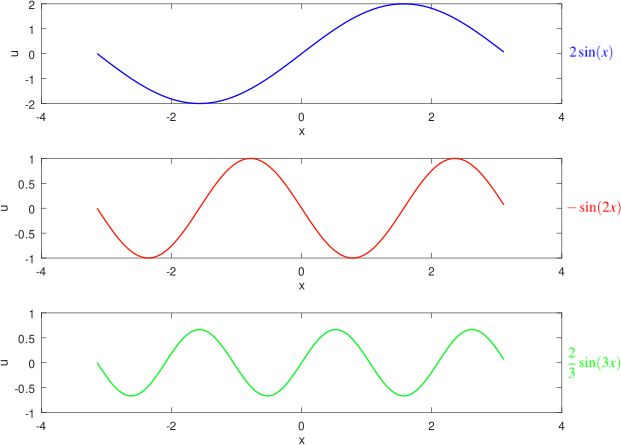
_{Gráficas de las funciones del desarrollo de la serie Fourier. Elaborado con GNU Octave, por @abdulmath.}
Ahora, grafiquemos la suma de estos factores y obtenemos la suma parcial S₃, en el gráfico anexo:


_{Gráficas de las sumas parciales del desarrollo de la serie Fourier. Elaborado con GNU Octave, por @abdulmath.}
Si ampliamos las sumas parciales de la serie de Fourier, por ejemplo tomamos S₆ y S₉, al graficarlas obtenemos el siguiente resultado:


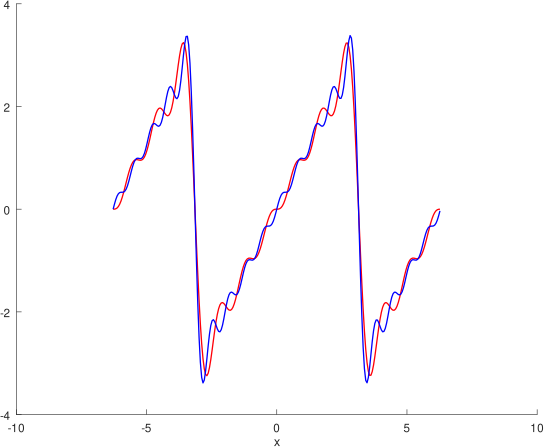
_{Gráficas de S6 en rojo y S9 en azul, de la serie Fourier. Elaborado con GNU Octave, por @abdulmath.}

Es importante resaltar que en ambos ejemplos la serie de Fourier converge a la función f en los puntos de continuidad.

---

---

Queridos amigos y lectores, espero hayan disfrutado y aprendido acerca de la Series de Fourier y algunos ejemplos en GNU Octave. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso y hermoso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

• Folland G. B., Fourier Analysis and its Applications, Brooks/Cole Publishing Company, 1992.
• Folland G. B., Real Analysis, John Wiley, New York, 1984.

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, GNU Octave, , GIMP e Inkscape.

---

---

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

_{Imagen diseñada con GIMP y elaborada por @abdulmath.}