Modelos matemáticos aplicados a la Mécanica Aplicada | Introducción

Saludos queridos lectores, bienvenidos nuevamente a mi Blog. Cuando hablamos de Matemáticas la primera reacción es de temor, terror, desagrado para las personas que no les interesa el tema, más sin emabrgo, las Matemáticas es parte fundamental para muchas ciencias y sobre todo de la ingeniería. Estudiar las Matemáticas, requiere hacer uso del razonamiento lógico, para lograr en la práctica el desarrollo del razonamiento riguroso con objetos y estructuras puramente abstractos. Así, en esta oportunidad hablaremos un poco de los Modelos matemáticos aplicados a la Mécanica Aplicada. La Mecánica Aplicada es la matemática aplicada a aquellas áreas problemáticas de la ciencia que surgen de las consideraciones de problemas continuos. Por lo tanto, a manera práctica, se fija una visión macroscópica del problema en cuentión, en vez de una visión atómica o cuántica del fenómeno y se presta atención a aquellas áreas en las que las observaciones o experimentos son reproducibles, y los datos medidos están disponibles de alguna manera. Uno de los objetivos fundamentales es el de demostrar la capacidad de formular problemas en Mecánica Aplicada. En realidad, es el de demostrar el poder de las matemáticas y la diversidad de sus aplicaciones, con la intención de estimular la construcción de modelos de nuevas situaciones.

Esta publicación esta dirigida a estudiantes, profesionales e investigadores en específico en el área de las Matemáticas Aplicadas e Ingeniería, y público interesado en estos temas interesantes para el entendimiento de buena parte del medio que nos rodea día a día. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.

La Mecánica Aplicada es la matemática aplicada a aquellas áreas problemáticas de la ciencia que surgen de las consideraciones de problemas continuos. Por lo tanto, a manera práctica, se fija una visión macroscópica del problema en cuentión, en vez de una visión atómica o cuántica del fenómeno y se presta atención a aquellas áreas en las que las observaciones o experimentos son reproducibles, y los datos medidos están disponibles de alguna manera. Uno de los objetivos fundamentales es el de demostrar la capacidad de formular problemas en Mecánica Aplicada. En realidad, es el de demostrar el poder de las matemáticas y la diversidad de sus aplicaciones, con la intención de estimular la construcción de modelos de nuevas situaciones.

El fin es construir una simulación matemática, o modelo, de un fenómeno científico dado, que concuerde con las mediciones existentes con una precisión especificada y que pueda utilizarse con confianza para predecir observaciones y comportamientos futuros. Partiendo de este punto de vista continuo, los modelos matemáticos implicarán naturalmente relaciones entre las funciones continuas del espacio y el tiempo que describen la aplicación de los principios científicos fundamentales de homogeneidad, isotropía y conservación a un problema dado.

El ejemplo más simple y quizás el más estudiado es el de la 2^da Ley de Movimiento de Newton para una partícula, el cual tiene una expresión matematica dada por:

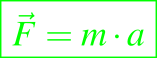
el cual conduce al modelo para una partícula que cae libremente por la gravedad,


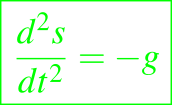
y predice que

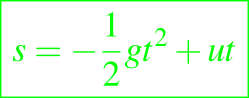
Por lo tanto, para lograr el éxito de la Mecánica Aplicada se necesitan dos habilidades opuestas pero complementarias, a saber, la capacidad de formular un problema dado en términos matemáticos apropiados y conocimientos suficientes para obtener información útil de ese modelo matemático.

La habilidad en la formulación radica en encontrar un modelo que sea lo suficientemente simple como para dar información útil fácilmente, pero que sea a la vez lo suficientemente diverso como para dar toda la información requerida con la suficiente precisión.

Un modelo puede ser apropiado en una serie de circunstancias, pero no tiene valor en otras porque es demasiado complicado o demasiado simple. Una vez que un modelo está bien establecido, rara vez se presenta en un libro de texto de tal manera que el lector pueda apreciar tanto las repetidas modificaciones hechas a modelos anteriores menos
satisfactorias, como la interacción entre estos modelos anteriores, su análisis y la comparación de la predicción con el experimento. El uso de la analogía entre modelos bien establecidos y nuevos problemas es claramente una ayuda muy valiosa

Si tenemos un problema macroscópico, el mismo tendrá en general una serie de características físicas cuantitativas, que varían en el espacio y el tiempo, a las que pueden asignarse símbolos matemáticos. Desde el punto de vista físico, un nivel macroscópico, es aquel donde la descripción de la posición o estado físico concreto de las partículas que integran el cuerpo a describir, puede ser expresado como una ecuación de estado que solo incluye magnitudes extensivas e intensivas.

Entonces las características pueden ser representadas por cantidades escalares, vectoriales o tensoriales y serán funciones de variables espaciales y temporales que son continuas y diferenciables excepto en superficies especiales. Estas cantidades estarán relacionadas por las leyes físicas fundamentales y dicha relación introducirá un número de constantes físicas medibles.

Cualquier fenómeno observado dependerá de las características físicas y constantes, pero en una situación dada puede no estar claro cuáles son las importantes. Por lo tanto, al intentar construir un modelo, hay que juzgar qué características incluir y cuáles no incluir. Si se omite una característica importante, 0entonces el modelo no describirá el fenómeno observado con la suficiente precisión o el modelo puede no ser autoconsistente. En algunos casos, si se incluyen características innecesarias, el modelo será más difícil de resolver debido a su mayor complejidad. Por lo tanto, es recomendable plantear un modelo con un enfoque simple con un mínimo de características incluidas en el primer intento, y características adicionales añadidas, si es necesario, una por una.

Así debería ser posible estimar el efecto de las características adicionales sobre los resultados del modelo original. Esto se hace normalizando el problema, es decir, definiéndolo en términos de variables no dimensionales cuya escala típica es de orden uno, y la magnitud relativa de los diferentes efectos físicos se mide mediante parámetros no dimensionales o grupos sin dimensión.

Un buen ejemplo es el de la mecánica de fluidos, donde las ecuaciones de Navier-Stokes para el flujo de un fluido viscoso incompresible proporcionan un modelo bien establecido. Las cantidades desconocidas son la velocidad q, la presión p y la temperatura T como funciones de las variables espaciales x y el tiempo t, donde los vectores tienen tres componentes. La aplicación de las leyes físicas de conservación de masa, el impulso y la energía, conduce al siguiente modelo:

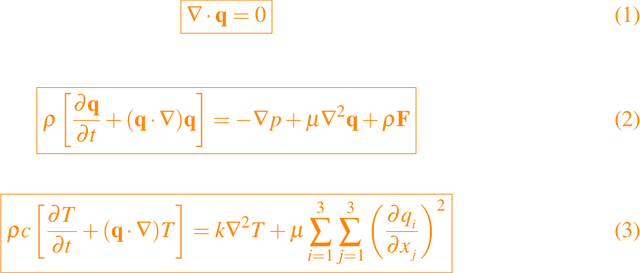
donde las constantes implicadas en las ecuaciones anteriores son: la densidad ρ, el coeficiente de viscosidad p, el calor específico c, la conductividad k, y si la fuerza del cuerpo F la cual se debe a la gravedad, y la aceleración gravitacional g.

En la ecuación dada en (2) los efectos físicos modelados son la inercia, las fuerzas viscosas y la gravedad; en la ecuación dada en (3) son la convección de calor (a veces llamada advección), la conducción de calor y la disipación viscosa.

En este modelo las variaciones en la densidad y el coeficiente de viscosidad son ignoradas, y la tensión del fluido depende linealmente de la velocidad de deformación, por lo que para determinar si se pueden ignorar más efectos físicos, se deben elegir escalas o valores de referencia típicos para cada variable, de manera que el problema pueda normalizarse. Para ello se requiere que el problema se le agreguen las condiciones de contorno.

Las condiciones de contorno adecuadas deben ser tales que conduzcan a un problema de valor en la frontera bien planteado (es decir, uno con solución única) para por lo menos un rango de valores de las constantes involucradas. Suponiendo que se dan las condiciones adecuadas, estas condiciones contendrán valores de referencia o escala para las variables, por ejemplo U para q, L para x, L/U para t, y T₁ - T₀ para T, donde T₀ es la temperatura ambiente. Si entonces definimos las variables no dimensionales por

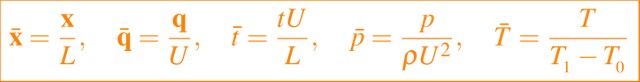
y así las ecuaciones del modelo (1) - (3) se transforman en las siguientes ecuaciones


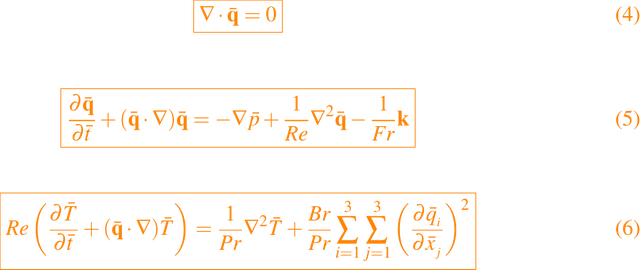
donde el operador nabla (∇) es con respecto a la variable x̄ y k es un vector unitario en la
dirección vertical ascendente. Se necesitan cuatro parámetros no dimensionales, aunque son posibles combinaciones claramente diferentes. Se elige el número de Reynolds, dado por


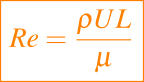
que compara los efectos de la inercia y la viscosidad, el número de Froude


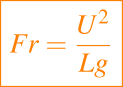
el cual compara la inercia y la gravedad, el número de Prandtl


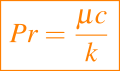
el mismo compara la escala de tiempo de la viscosidad con la de la conducción de calor, y el número de Brinkman


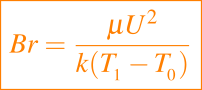
el mismo compara la disipación de la viscosidad del calor con la conducción de calor, otro parámetro, que se utiliza comúnmente, compara la escala de tiempo inercial con la de conducción y es el número de Peclet

Los valores numéricos de estos números deben ser establecidos para cualquier problema dado, y uno o más de ellos pueden ser muy pequeños o grandes. Así, para un número de Froude grande, los efectos de la gravedad pueden ser ignorados, ya que solo aparecen en un solo término con un pequeño coeficiente; para un número de Brinkman pequeño, la disipación puede ser descuidada en comparación con la conducción de calor y un modelo más simple derivado. Sin embargo, puede ser necesario, si no hay una elección obvia de la escala, reescalar una o más de las variables antes de descuidar los términos multiplicados por pequeños parámetros.

Así si Re << 1,además de 1/Fr y <Br << 1, el término de presión desaparecerá al usar Re = 0 y no será posible satisfacer todas las condiciones de contorno porque el orden del sistema de ecuaciones se ha reducido. La razón es que la escala de presión se basó en la inercia más que en las fuerzas viscosas, y es necesario una reescala, a saber

En este caso, con Re = 0 = Br = 1/Fr, y Pr un valor no grande para que Pe = 0, el modelo se
reduce a


Sin embargo, la ecuación dada en (7) no contiene ninguna derivada temporal, es decir, describe una situación instantánea en la escala de tiempo de inercia. Una escala de tiempo viscosa sería


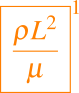
con


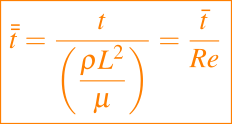
luego, el modelo se convierte en

También puede darse el caso de que la escala de tiempo de temperatura t₀ no sea ni la inercia ni la escala de tiempo de la viscosidad, la ecuación dada en (9) debe ser reemplazada por

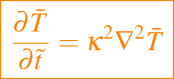
donde


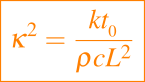
es la difusividad no dimensional.

_{¹ Las dimensiones de la viscosidad cinemática 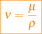y la difusividad dimensional son (longitud)²/tiempo.}

Queridos amigos y lectores, espero hayan disfrutado de una nueva publicación donde las matemáticas tienen sus aplicaciones en otros campos de la ciencia los cuales son de mucho interés en general. Espero que la misma haya sido de su agrado, y pueda servir de una ventana de apoyo para visualizar las estrechas relaciones que existen en particular entre las ciencias, así como se puede contextualizar las mismas teorías en la ingeniería, gracias por tomar un poco de su tiempo y poder disfrutar un poco más del maravilloso mundo de las matemáticas y las ciencias básicas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

1. Bender, C. M. and Orszag, S. A. Advanced mathematical methods for scientists and engineers. McGraw-Hill, New York. 1978.
2. Courant, R. and Hilbert, D. Methods of mathematical physics, vol. I. Interscience, New York. 1976.
3. Landau, L. D. and Lifshitz, E. M. Fluid mechanics. Pergamon, London. 1963.
4. Stakgold, I. Green's functions and boundary value problems. Wiley-Interscience, New York. 1979.

La imagen de fondo de la portada es una imagen de libre uso tomada de y editada con GIMP por @abdulmath. Las imágenes son todas de libre uso, tomadas de y editadas y tratadas con GIMP. Los títulos, imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, LaTeX2e, Inkscape y GIMP.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.