Modelos Matemáticos Clásicos en Mécanica Aplicada

Esta publicación esta dirigida a estudiantes, profesionales e investigadores en específico en el área de las Matemáticas Aplicadas e Ingeniería, y público interesado en estos temas interesantes para el entendimiento de
buena parte del medio que nos rodea día a día. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.



El modelo clásico para el flujo de un fluido viscoso incompresible ya ha sido establecido en las ecuaciones siguientes:
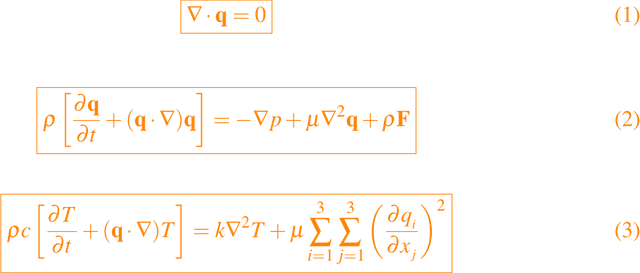
que se denominan ecuaciones de Navier-Stokes. Inherente a este modelo es la suposición newtoniana de que el tensor de esfuerzo {σij} es una función lineal del tensor de velocidad de deformación, donde
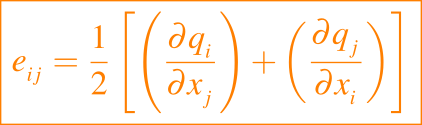
Así, al derivar la ecuación dada en (2) obtenemos un balance de momento de la forma
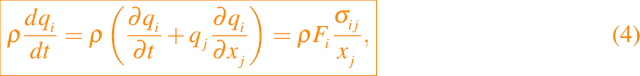
se ha asumido una ley constitutiva de la forma

En estas ecuaciones se utiliza la función delta de Kronecker δij, y donde μ, y ρ son constantes. Se supone que se da la fuerza del cuerpo, de modo que las ecuaciones (1) y (3) constituyen cuatro ecuaciones escalares para cuatro incógnitas escalares q y p. La ecuación (3) es entonces una ecuación escalar adicional para T. En física o matemáticas generalmente, esperamos poder prescribir que q = 0 en la frontera espacial fija, junto con los valores iniciales, y obtener una solución al menos durante un intervalo de tiempo acotado. La prueba de la existencia y la singularidad es difícil, y ciertamente se acota a un tiempo determinado. Muchos flujos se vuelven inestables después de un tiempo finito, exhibiendo el fenómeno de turbulencia, y el modelo es entonces inadecuado; por lo tanto, no necesariamente pueden existir flujos estables y constantes. Como sabemos, las soluciones dependen del parámetro Re, que no es otro que el número de Reynolds, y puede demostrarse que en una configuración dada el flujo constante será estable si el número de Reynolds es suficientemente pequeño [<O(103)], lo que concuerda con las observaciones. Por lo tanto, el modelo sólo es apropiado para flujos laminares cuando el número de Reynolds es inferior a su valor crítico. Para una discusión detallada de este fenómeno extremadamente complejo el lector puede consultar a Landau y Lifshitz (1963).
Las ecuaciones de Navier-Stokes son difíciles de resolver incluso para flujos constantes bidimensionales debido a la no linealidad en el término convectivo
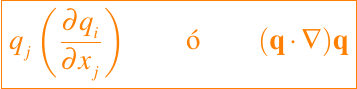
en la notación vectorial. El modelo de flujo lento, es decir, cuando el número de Reynaolds tiende a cero, viene dado por las ecuaciones (1) y

y en variables dimensionales se reduce a

o eliminando p, obtenemos
Para una situación bidimensional se puede introducir una función de flujo ψ(x, y) donde q = curl(0, 0, ψ) y las ecuaciones vectoriales se reducen a la ecuación biarmónica para ψ, a saber

Las condiciones de contorno apropiadas serían prescribir la velocidad, equivalente a la prescripción de ∇ψ, en un contorno espacial. La prescripción de la tensión normal y tangencial, que es la condición física necesaria en la frontera libre entre dos fluidos, o más bien entre un fluido y una región de presión constante que modela un gas, es menos simple. El modelo de flujo lento está bien planteado, y se ha dedicado un esfuerzo matemático considerable a la construcción de soluciones, tanto en términos de funciones simples utilizando métodos variables complejas como de métodos numéricos.
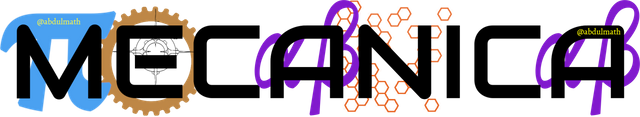

El límite alternativo es considerar flujos laminares con el número de Reynolds grande, lo que es equivalente a omitir la viscosidad; esto lleva a la ecuación de Euler para un fluido no viscoso,

donde F es cualquier fuerza cuerpo por unidad de masa. Junto con ∇ · q = 0 estas son cuatro ecuaciones escalares para cuatro incógnitas, pero el orden de la ecuación ha disminuido debido al haber omitido el término ∇2q de la ecuación (2). Por lo tanto, no es sorprendente que la velocidad ya no pueda ser especificada en una frontera fija. Físicamente, sin viscosidad, se permite el deslizamiento y no podemos esperar especificar la velocidad tangencial e la frontera. Por lo tanto, una condición de contorno apropiada en un contorno fijo es que qn, el componente normal de q, es igual a cero; esto, junto con una condición inicial, completa el modelo de no viscosidad.
Debido a la no linealidad, las soluciones generales no son fáciles de construir; pero es posible derivar el notable resultado de que si la vorticidad ζ = curl qes inicialmente cero en una región dada, entonces permanecerá cero para las mismas partículas del fluido durante todo el tiempo. Así, todos los flujos que parten de condiciones de reposo o constantes son irrotacionales, es decir, tienen un curl q = 0. Esto conduce a la introducción de un potencial de velocidad φ tal que q = grad φ, donde φ satisface las siguientes ecuaciones
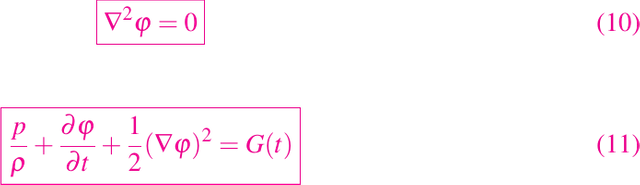
donde G debe determinarse a partir de una condición inicial. La no linealidad aparece ahora sólo en la ecuación de Bernoulli (11), y si
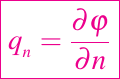
se especifica en la frontera espacia del problema para φ lineal e independiente de t, con la no linealidad interviniendo sólo en la integración de la ecuación (11) con respecto al tiempo para obtener la presión. Para flujos bidimensionales existe una función de flujo Ψ y ∇2Ψ = 0, de modo que un potencial complejo ω = ψ + iΨ puede ser definido y una variedad de soluciones simples desarrolladas por el método de variable compleja.
La relevancia de este modelo irrotacional no viscoso se acota a regiones en las que la viscosidad es insignificante. Para muchos fluidos la viscosidad es muy pequeña, pero sin embargo no se puede descuidar en una región adyacente a una frontera sólida, donde ocurre una capa límite a través de la cual la velocidad tangencial se ajusta rápidamente de cero a su valor de no viscosidad prevista. Sin embargo, la vorticidad se genera en esta capa límite y se convecciona con las partículas fluidas, de modo que se forma un despertar en el que la vorticidad no es cero. En el caso de los cuerpos revestidos de corriente, esta estela es delgada y no afecta materialmente al flujo total. Sin embargo, para un cuerpo de acantilado, la capa límite se separará de su superficie para formar una estela extensa que alterará las regiones de flujo irrotacional.
Por lo tanto, el modelo de flujo no viscoso, sin más modificaciones, sólo es relevante para los cuerpos de flujo que pasan por encima de los cuerpos que son aerodinámicos para producir estelas delgadas. También es relevante para el flujo transfronterizo, es decir, el flujo adyacente a una región de presión constante. En tal frontera, cuya posición será desconocida y parte del problema, la velocidad normal relativa será cero y se prescribirá la presión de la continuidad de la tensión normal. La tensión tangencial es necesariamente cero por la falta de viscosidad, y no se necesita ninguna capa de ajuste en dicha frontera.
Si la frontera libre z =η(x, y, t) modela la superficie de una gran extensión de agua profunda que se mueve bajo la gravedad, entonces el problema del valor en la frontera para φ y η es
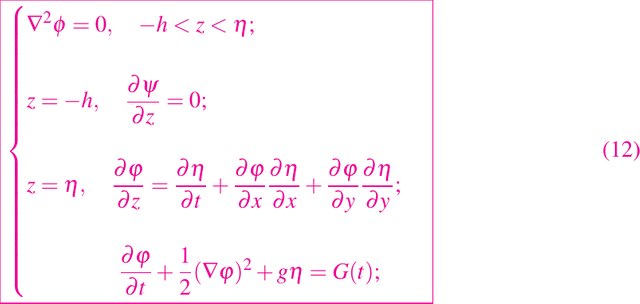
donde por simplicidad h es constante y se dan las condiciones iniciales. Este es un problema difícil debido a las condiciones de fronteras no lineales, pero existe una solución por un tiempo limitado. Sin embargo, si las perturbaciones de la superficie son pequeñas para que las condiciones se puedan linealizar, entonces las ecuaciones en (12) se reduce al modelo muy exitoso para las ondas de agua en la forma
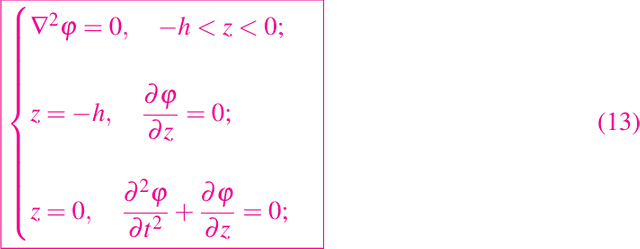
donde z = 0 es la altura media de la superficie. Para más detalles sobre la relevancia y el uso de este modelo, podemos consultar a Ockendon y Tayler (1983).
Tanto en los modelos viscosos como en los no viscosos, la ecuación de energía (3) no ha interactuado con las ecuaciones de continuidad y momento, es decir, que el problema puede resolverse para el flujo con respecto a la ecuación de energía. Para el modelo no viscoso, la ecuación (3) se reduce a

y si el número de Peclet es grande, el término de conducción puede ser omitidao, y la temperatura es constante para cada partícula de fluido. Cerca de una frontera en la que se prescribe la temperatura habrá una capa límite a través de la cual la temperatura se ajusta desde el valor dado hasta el valor de convección del fluido.
Para un fluido compresible la ecuación de energía es parte del problema de flujo y consideramos un gas ideal, que es no viscoso, no conductor de calor, y tiene una ley de gas p = ρRT donde R es una constante. Las ecuaciones de continuidad, momento y energía son en este caso
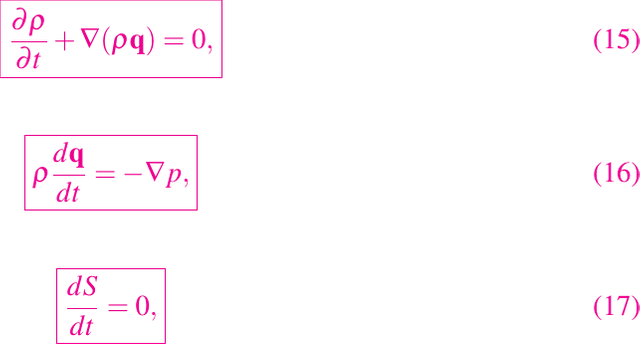
donde la entropía S es proporcional a p/ργ y γ es la relación constante de calores específicos en el gas. Este es el modelo de flujo entrópico, y para los flujos de condiciones uniformes la entropía S es una constante universal y el flujo es homentrópico. Esto implica que p = p(ρ), y eliminando p el problema se reduce a cuatro ecuaciones escalares para cuatro incógnitas q y ρ. Por lo tanto, esperamos un problema bien planteado, al menos por un tiempo limitado, dadas las condiciones espaciales y de contorno iniciales adecuadas. Sin embargo, el modelo es altamente no lineal y sólo se pueden encontrar unas pocas soluciones de forma cerrada, para más el lector puede ver Ockendon y Tayler (1983).
Asumiendo que sólo hay pequeñas perturbaciones q sobre un estado de reposo con densidad ρ0 y presión p0, el problema puede ser linealizado en la forma
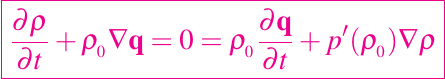
El flujo de perturbación es irrotacional de modo que q = ∇φ, y eliminando p

Esta es la ecuación para las ondas acústicas, es decir, la propagación de pequeñas perturbaciones de presión en el gas, y la velocidad del sonido es

Es interesante observar que los tres modelos más simples descritos anteriormente, a saber, la ecuación (10) para un fluido incompresible no viscoso, la ecuacíión (18) para flujos compresibles con pequeñas perturbaciones y la ecuación (14) para la distribución de la temperatura cuando el flujo es insignificante, tienen ecuaciones que la rigen las cuales son ecuaciones diferenciales parciales escalares canónicas de segundo orden de tipo elíptico, hiperbólico y parabólico, denominadas ecuación de Laplace, la ecuación de onda y la ecuación de difusión respectivamente.
Las soluciones de estas ecuaciones proporcionan información valiosa sobre las aplicaciones de los modelos. Las aplicaciones, sin embargo, proporcionarán resultados que proporcionarán información sobre las propiedades cualitativas esperadas de esas ecuaciones. Por lo tanto, existe una interacción entre los resultados probados relacionados con las ecuaciones del modelo y las observaciones de la aplicación del modelo, en beneficio mutuo tanto de la teoría pura como de la aplicación. Además, es probable que la ecuación aparezca como un modelo para una aplicación diferente, y se puede establecer una analogía entre las dos aplicaciones a través de las propiedades de la ecuación.
Queridos amigos y lectores, espero hayan disfrutado de una nueva publicación donde las matemáticas tienen sus aplicaciones en otros campos de la ciencia los cuales son de mucho interés en general. Espero que la misma haya sido de su agrado, y pueda servir de una ventana de apoyo para visualizar las estrechas relaciones que existen en particular entre las ciencias, así como se puede contextualizar las mismas teorías en la ingeniería, gracias por tomar un poco de su tiempo y poder disfrutar un poco más del maravilloso mundo de las matemáticas y las
ciencias básicas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Bender, C. M. and Orszag, S. A. Advanced mathematical methods for scientists and engineers. McGraw-Hill, New York. 1978.
- Courant, R. and Hilbert, D. Methods of mathematical physics, vol. I. Interscience, New York. 1976.
- Landau, L. D. and Lifshitz, E. M. Fluid mechanics. Pergamon, London. 1963.
- Stakgold, I. Green's functions and boundary value problems. Wiley-Interscience, New York. 1979.
La imagen de fondo de la portada es una imagen de libre uso tomada de Pixabay y editada con GIMP por @abdulmath. Las imágenes son todas de libre uso, tomadas de Pixabay y editadas y tratadas con GIMP. Los títulos, imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, LaTeX2e, Inkscape y GIMP.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea
apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.



Excelente aplicación matemática mi estimado amigo @abdulmath. La viscosidad es una propiedad de los fluidos líquidos que se rige por diversos comportamientos, como el modelo plástico de bingham, el de ley de potencia entre otros. Los modelos explicados por tí en esta publicación resalta la importancia de los modelos matemáticos en la ingeniería.
Es fundamental el estudio de la viscosidad y los modelos matemáticos que la rigen, ya que dentro de la ingeniería en sus diversas ramas existen diversidad de fluidos, lo que se transforma en una diversidad de modelos. Gracias por compartir este excelente contenido. Saludos.
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by abdulmath from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Hola, amigo @abdulmath . Te felicito por incursionar en el campo de la ingeniería y aportar tus excelentes conocimiento matemáticos sobre tópicos relativos a los sistemas hidráulicos, materia que me apasiona. Todos tus artículos constituyen para mí una "Referencia Bibliográfica" que me permito consultar cuando lo requiero. Dios te bendiga y proteja siempre, HERMANO. AMÉN.
Hola amigo @reyito, muchas gracias por tus palabras, muy contento que poses por mi blog, y de tus buenas apreciaciones. De verdad que es para mi un honor que utilizes mis artículos para consulta.
Saludos y un muy fuerte abrazo. Dios te Bendiga. Amén.
Ya se quien pedirle apoyo en el área de matemáticas! XD
@abdulmath está publicación me encantó, sé que es super profundo indagar en las razones de ser de los modelos matemáticos, a veces sólo nos enfocamos en aplicar y encontrar el resultado, ir a una tabla y buscar variales, correr el software pero cuando se análiza desde la raíz creo que se podría entender de forma más amplia y completa.
La matemática es maravillosa, y la mecánica de fluidos es encantadora. Entenderlas requiere pasión y eso te sobra querido amigo.
Te envío un saludo en un flujo estable y espero que el tiempo no lo cambie tan rapido.
¡Felicidades, #proconocimiento te valoró!
Has sido reconocido(a) por tu buen post por el Comité de Arbitraje y Valoración del Proyecto Conocimiento @proconocimiento.
Apoyamos y vloramos tu esfuerzo...

Proyecto Conocimiento es parte de la comunidad @provenezuela.
Pioneros en la plataforma #steemit en el reconocimiento y valoración a la Producción Intelectual en habla hispana.
Próximamente te estaremos exigiendo tu suscripción a nuestro trail, para poder optar a nuestro voto. Puedes suscribirte a través de la herramienta "SteemAuto".
Hola @ abdulmath, te felicito. Excelente revisión sobre Física-Matemática... Pocos Matemáticos AMIGOS conozco que se atrevan abordan estos temas... Exitos...