Modelos Continuos de Población | Análisis Cualitativo

Saludos queridos lectores, bienvenidos nuevamente a mi Blog. Las matemáticas hoy en día desempeñan un papel cada vez más importante y relevante en las ciencias, en particular en las ciencias biológicas, lo que ha provocado una gran confusión en las fronteras entre las disciplinas científicas y un gran auge por el resurgimiento del interés hacia las técnicas modernas y clásicas de las matemáticas aplicadas. Continuando con el tema que he venido desarrollando en mis dos ultimas publicaciones (La Biología y las Matemáticas y Modelos Continuos de Población | El modelo Crecimiento exponencial y El Modelo Logístico de Población), en esta oportunidad trataremos en el enfoque o análisis cualitativo de los modelos continuos de población. La palabra Cualitativo es un adjetivo que se usa para hacer referencia a aquellas cosas relacionadas con la cualidad, como por el ejemplo, la forma de ser, o propiedades de algún objeto. Por lo tanto un análisis cualitativo, es el encargado de mostrar las características de ese algo que se este estudiando. Es por ello entonces que podemos enfocar lo cualitativo con la calidad, y lo cuantitativo con la cantidad.

Esta publicación esta dirigida a estudiantes, profesionales e investigadores en especifico en el área de las ciencias Biológicas, o Matemáticas, y al publico interesado en estos temas interesantes para el entendimiento de parte del medio que nos envuelve en el día a día. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.

Cuando usamos un modelo logístico en la práctica, normalmente se asume que una población está efectivamente descrita por un modelo logístico y luego se intenta elegir los parámetros r y K y el tamaño inicial de la población x₀ para dar el mejor ajuste con los datos experimentales. Es importante recordar que los valores de r, K y x₀ están sujetos a un error, el cual puede ser de diferentes índoles. Sin embargo, los errores en r y x₀ no afectan nuestra predicción del tamaño final de la población K. La propiedad de que un pequeño cambio en el tamaño inicial x₀ de una solución tiene solo un pequeño efecto en el comportamiento de la solución, ya que el tiempo t tiende a infinito, se le llama estabilidad de la solución.

Necesitaremos la estabilidad de cualquier solución a la que le atribuiremos su importancia biológica; si una pequeña perturbación puede causar un gran cambio en la solución, no es razonable considerar que la solución sea significativa.

También es importante resaltar que el modelo logístico es una forma asumida, no una consecuencia de una ley fundamental. Quisiéramos considerar clases más grandes de modelos y examinar las propiedades que son válidas para estas clases más grandes en lugar de aquellas propiedades que dependen de las características específicas del modelo logístico. Se dice que una propiedad que se mantiene para un gran número de modelos es robusta, para indicar que es más probable, en cierto sentido, que tenga significado biológico.

La información que derivamos sobre el comportamiento de las soluciones del modelo logístico se obtuvo a partir de la solución explícita por el método de separación de variables. Ahora bien, si deseamos encontrar propiedades robustas debemos aprender a deducir las propiedades de las soluciones a partir de la ecuación diferencial directamente, sin depender de expresiones analíticas para las soluciones.

La derivada de la solución x(t) en un punto (t, x(t)) es el lado derecho de la ecuación logística

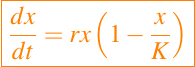
Esto es positivo si 0 < x < K, cero si x = 0 ó x = K, y negativo si x < 0 ó x > K. Así, una solución x(t) es una función creciente en el tiempo t cuando 0 < x(t) < K y una función decreciente en el tiempo t cuando x(t) > K. El caso x(t) < 0 no lo tomamos en cuanta ya que no tiene ningun tipo de importancia biológica. Las constantes x = 0 y x = K son soluciones de la ecuación logística. Si derivamos la ecuación logística con respecto a t obtenemos lo siguiente


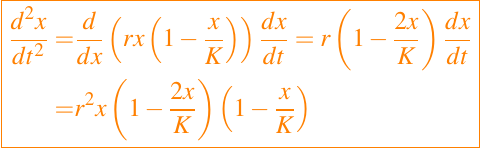
Luego de allí deducimos que la segunda derivada cambia de signo cuando a cruza la línea horizontal x = K /2 y por lo tanto, una solución que cruza esta línea tiene un punto de inflexión en el cruce. Las curvas de la solución podemos verlas en la figura anexa.


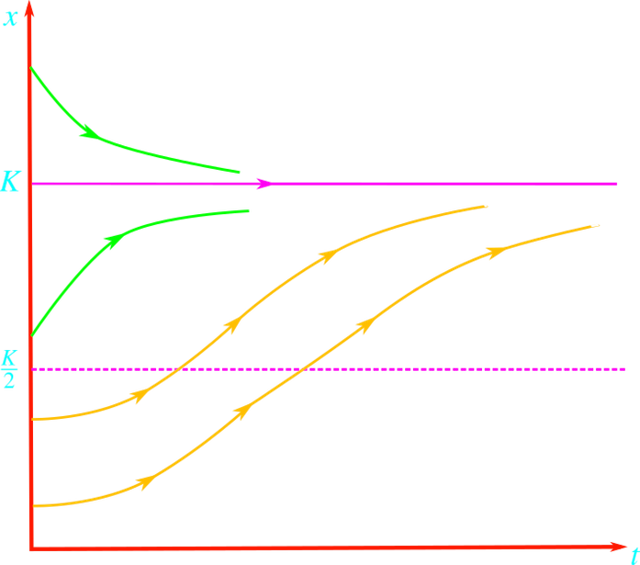
_{Curvas de solución de la ecuación logística. Elaborada en Inkscape por @abdulmath.}

Si x(t) < K para algún valor del tiempo t entonces la gráfica de x(t) no puede cruzar la línea x = K y la misma creciendo para todo valor del tiempo t. De esta manera, decimos que x(t) tiende al límite cuando t tiende a ∞, pero los únicos límites posibles son para los valores de x donde el lado derecho de la ecuación diferencial es cero, es decir, cuando x = 0 ó x = K. Ahora dado que las soluciones cercanas a x = 0 no pueden acerca a cero, pero deben tender a K cuando t tiende a ∞. Una solución x(t) que está por encima del valor K, decrece para todo valor del tiempo t y con un argumento similar debe tender a K cuando t tiende a ∞.

Así, vemos que cada solución no negativa excepto la solución constante x = 0 tiende a K cuando t tiende a ∞, y hemos obtenido esta información sin resolver explícitamente la ecuación diferencial. El método que hemos utilizado puede adaptarse a ecuaciones diferenciales de primer orden más generales.

Consideraremos las ecuaciones diferenciales de primer orden autónomas es decir, las ecuaciones de la forma

en el que el lado derecho no contiene la variable independiente t. A veces escribiremos la ecuación en la forma


donde r(x) representa la tasa de crecimiento per cápita. Definimos un equilibrio de la ecuación diferencial dada en (1), denotado por x_∞ un valor tal que f(x_∞) = 0. Un equilibrio corresponde a una solución constante de la ecuación diferencial, dada por x(t) = x_∞.

Si x(t) es una solución de una ecuación diferencial x' = f(x) que tiende a un límite cuando t tiende a ∞ entonces no es difícil mostrar que su valor límite debe ser un equilibrio. De hecho, para una ecuación diferencial de primer orden cada solución debe tender a un equilibrio cuando t tiende a ∞ o no esta acotada. Sin embargo, no todo equilibrio es un límite de soluciones no constantes. Por ejemplo, la única solución de la ecuación logística que tiende a cero cuando t tiende a ∞ es la misma solución cero.

Para describir el comportamiento de las soluciones cerca de un equilibrio, introducimos el proceso de linealización. Si x_∞ es un equilibrio de la ecuación diferencial x' = f(x) de modo que f(x_∞) = 0, se realiza un cambio de la variable, es decir, llamemos u(t) = x(t) - x_∞, la cual representa la desviación de la solución del valor de equilibrio. Al sustituirlo en la ecuación obtenemos

y la aplicando el teorema de Taylor tenemos


para algún valor de c entre x_∞ y x_∞ + u(t). Usamos f(x_∞) = 0 y escribimos


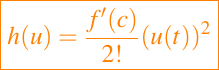
Entonces podemos reescribir la ecuación diferencial x' = f(x) en


La función h(u) toma valores pequeños para valores |u| pequeños, es decir, h(u)/u tiende a 0 cuando u tiende a 0; más precisamente, por cada ε > 0 existe δ > 0 tal que |h(u)| < ε|u| siempre que |u|<δ. La linealización de la ecuación diferencial en el equilibrio x_∞ se define como la ecuación diferencial lineal homogénea


obtenida para dejar a un lado el término de orden superior h(u) en u' = f'(x_∞)u + h(u). La importancia de la linealización radica en el hecho de que el comportamiento de sus soluciones es fácil de analizar, y este comportamiento también describe el comportamiento de las soluciones de la ecuación original dada en (1) cerca del equilibrio.

Hemos establecido una forma que se generaliza fácilmente a los resultados para sistemas de ecuaciones diferenciales En la situación específica, la condición de que todas las soluciones de la linealización tiendan a cero es f'(x_∞) < 0. Para un equilibrio x_∞ con f'(x_∞) < 0 debemos tener que f(x) > 0 cuando x < x_∞ y f(x) < 0 para x > x_∞ si x está suficientemente cerca de x_∞. Por lo tanto, el campo de dirección es como se muestra a continuación

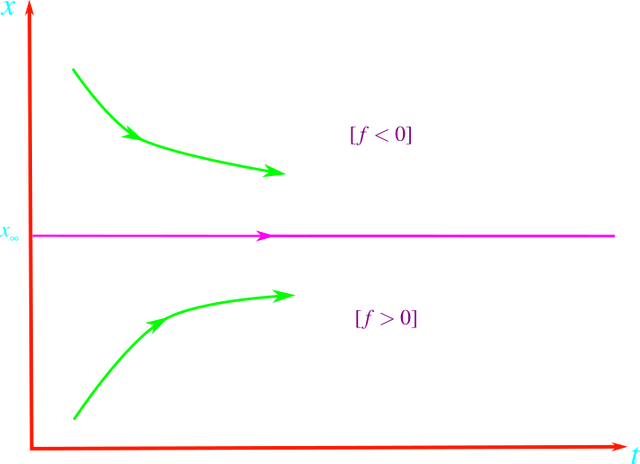
_{Campos de dirección de la ecuación autónoma.}

Una solución con x(0) > x_∞ es monótona, decreciente pero acotada por x_∞, y por lo tanto tiene un límite cuando t tiende a ∞. Como el único posible los límites de las soluciones son los equilibrios, tal solución debe tender a x_∞, siempre y cuando no existan otros equilibrios entre x(0) y x_∞. Con un argumento similar, una solución con x(0) < x_∞ crece monótonamente a x_∞ si no hay otra solución de equilibrio entre x(0) y x_∞. Por lo tanto, todas las soluciones con x(0) suficientemente cerca de x_∞ se aproxima a x_∞ cuando t tiende a ∞. De hecho, para la ecuación diferencial de primer orden podemos ser más precisos: Si x_∞ es un equilibrio con f'(x_∞) < 0 entonces cada solución cuyo valor inicial x(0) esté entre x_∞ y el siguiente equilibrio, en cualquier dirección, debe tender a x_∞ cuando t tiende a ∞.

Se dice que un punto de equilibrio x_∞ es estable si por cada ε > 0 existe δ > 0 de tal manera que |x(0) - x_∞| < δ implica |x(t) - x_∞| < t para todos t > 0.

Está implícito en esta definición que la existencia de la solución x(t) es requerida para t en el intervalo [0, ∞). Se dice que un equilibrio x_∞ es asintóticamente estable si es estable y si además|x(0) - x_∞| < δ lo cual implica que límite cuando t tiende a ∞ de x(t) es igual a x_∞.

Así, la estabilidad significa aproximadamente que un pequeño cambio en el valor inicial produce solo un pequeño cambio en la solución y esta condición es un requisito natural para que un equilibrio sea biológicamente significativo. Es posible que los sistemas tengan equilibrios para los cuales todas las soluciones que comienzan cerca del equilibrio terminan en el equilibrio, pero solo después de haber viajado fuera del equilibrio. Tal equilibrio no sería estable, pero nuestra definición de estabilidad asintótica requiere estabilidad para excluir esta posibilidad.

En aplicaciones biológicas normalmente se requerire estabilidad asintótica en lugar de estabilidad, tanto porque la estabilidad asintótica puede determinarse a partir de la linealización, mientras que la estabilidad no puede, y porque un equilibrio asintóticamente estable no se ve muy perturbado por una perturbación de la ecuación diferencial. En términos de estabilidad asintótica, se obtiene un resultado de inestabilidad correspondiente.

Ya hemos mencionado el modelo logístico, con

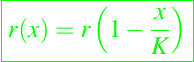
como ejemplo. Otros ejemplos que se han utilizado en los modelos de población incluyen los siguientes:

Al usar un modelo de este tipo para estudiar un problema de población, uno asumiría una forma particular para r(x), realizaría experimentos, y ajustaría los datos resultantes a esta forma para estimar los parámetros del modelo, y luego compararía otras observaciones con las predicciones del modelo para juzgar su validez.

Cada ecuación diferencial autónoma de la forma x' = f(x) o x' =xr(x) es de variables separables y por lo tanto puede resolverse en principio mediante integración. El lector debe observar que para cada uno de los ejemplos anteriores la integración necesaria es lo suficientemente complicada como para hacer atractivo un enfoque cualitativo.

Si en el modelo

la función r(x) es no negativa y decreciente para x en el intervalo [0, K] entonces se dice que es un modelo de compensación. Si la tasa de crecimiento per cápita r(x) está aumentando para valores pequeños de x, se dice que el modelo es un modelo de depensación. Si la tasa de crecimiento per cápita es realmente negativa para valores pequeños x, entonces se dice que el modelo es un modelo de depensación crítica. Mientras que los modelos de compensación son los más comúnmente examinados, tanto la depensación como la depensación crítica surgen en los estudios de pesca.

Un modelo de compensación se caracteriza por las siguientes condiciones

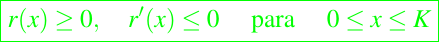
Para un modelo de depensación asumimos


Así, r(x) alcanza un máximo en K^∗, y como


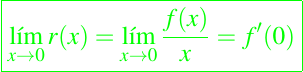
de ello se deduce lo siguiente f'(0) < r(K^∗ ). Así, la línea que une el origen con el punto (K^∗, f(K^∗)) en la curva de crecimiento y = f(x), que tiene pendiente r(K^∗), se encuentra por encima de la tangente a la curva de crecimiento en el origen. Además, dado que


tenemos


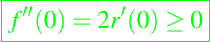
y


Esto muestra que la curva de crecimiento tiene un punto de inflexión a la izquierda de K^∗.

Para un modelo de depensación crítica asumimos

Bajo esta suposición no es difícil mostrar que la ecuación x' = f(x) tiene tres equilibrios: un equilibrio inestable en K⁰ y un equilibrio asintoticamente estable en 0 y K. Entonces, si el tamaño inicial de la población está por debajo de K⁰, la población se extinguirá. En el caso de la caza de depensación crítica, la caza puede llevar a una población a la extinción al reducir el tamaño de la población por debajo del nivel crítico K⁰, y esta tendencia a la extinción no se invertirá si la caza cesa. La extinción a través de la caza de la paloma mensajera en el siglo XIX y principios del XX de una población original de 7.000 millones de personas puede haber sido un ejemplo de depensación crítica. Esta propiedad a veces se llama el efecto Allee [Allee (1931)].

En los tres casos de compensación, depensación y depensación crítica la curva de crecimiento tiene las diferentes formas que se muestran en la figura anexa:

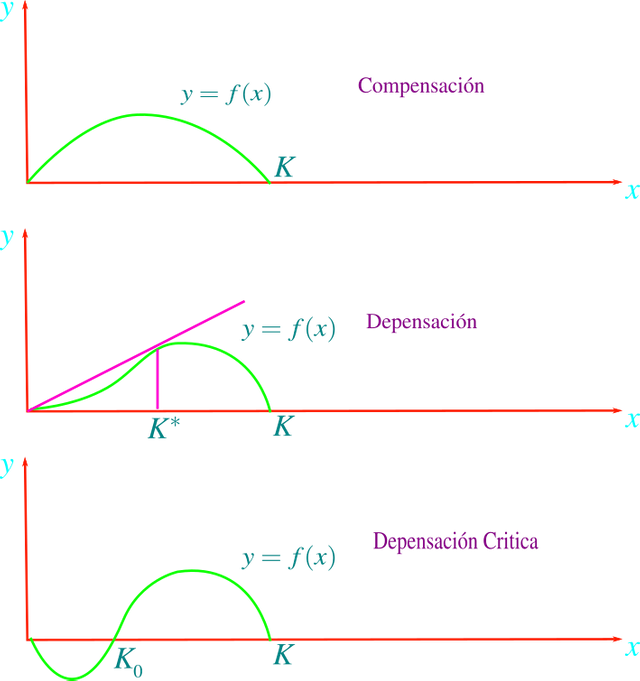
_{Curvas de crecimiento para los casos de compensación, depensación y depensación crítica. Elaborado con Inkscape por @abdulmath.}

En todos estos modelos hemos estado asumiendo tácitamente que la función f(x) en el lado derecho de la ecuación diferencial es exacta. Cualquier estudio realista reconocería que el modelo puede ser en el mejor de los casos una aproximación, y que en lugar de x' = f(x) deberíamos realmente estudiar una ecuación diferencial de la forma

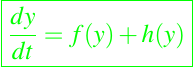
en el que el término h(y) representa el error cometido al asumir la forma específica f(y). Está en la naturaleza de h(y) que no puede ser conocido explícitamente. Así, en lugar de buscar fórmulas explícitas para las soluciones de y' = f(y) + h(y), debemos conformarnos con información cualitativa sobre las soluciones para un determinado número de funciones h(y).

Queridos amigos y lectores, espero hayan disfrutar de una nueva publicación donde las matemáticas tienen sus aplicaciones en otros campos de la ciencia los cuales son de mucho interés en general. Espero que la misma haya sido de su agrado, y pueda servir de una ventana de apoyo para visualizar las estrechas relaciones que existen en particular entre las ciencias, así como se puede contextualizar las mismas teorías en las ciencias sociales, gracias por tomar un poco de su tiempo y poder disfrutar un poco más del maravilloso mundo de las matemáticas y las ciencias básicas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

1. Anónimo, An Essay on the Principle of Population, as it affects the future improvement of society with remarks on the speculations of Mr. Godwin, 1798.
2. Cohen, J. E. How Many People Can the Earth Support? W. W. Norton and Company, New York-London, 1995.
3. Eugene M. Izhikevich. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. Massachusetts Institute of Technology, 2007.
4. Fred Brauer, Carlos Castillo-Chávez, Elmer De La Pava-Salgado, Kamal Barley, Carlos W. Castillo-Garsow, Diego Chowell, Baltazar Espinoza, Paula González Parra, Carlos Hernández Suárez, Víctor M. Moreno. Modelos de la propagación de enfermedades infecciosas. Universidad Autónoma de Occidente. Cali, Colombia. 2015

La imagen de fondo de la portada es una imagen de libre uso tomada de y editada con GIMP por @abdulmath. Las imágenes son todas de libre uso, tomadas de y editadas y tratadas con GIMP. Los títulos, imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, LaTeX2e, Inkscape y GIMP.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.