Interpolación Polinomial a Trozos usando el entorno GNU Octave | 2da Parte

Interpolación Cúbica de Hermite a Trozos
Ahora vamos a tratar a las funciones cúbicas por partes. Cuando aumentamos el grado, podemos obtener un ajuste más bajo en un conjunto dado de n puntos. La idea es interpolar tanto la función f como su derivada con una función cúbica en cada uno de los subintervalos dados.
Interpolación Cúbica de Hermite
Hasta ahora solo hemos considerado la interpolación de los valores de las funciones en distintos puntos. En el problema de interpolación de Hermite, tanto la función como su derivada son interpoladas. Para ilustrar la idea, consideramos la interpolación de la función f(z) = cos(z) en los puntos
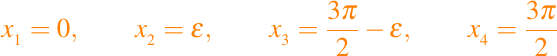
para un polinomio cúbico p3(z). Para valores de epsilon pequeños, notamos que p3(z) parece interpolar tanto la función f como s derivada f' en z = x0 y z = x4. La interpolación la mostramos en la figura siguiente, la cual obtenemos ejecutando el script anexo.
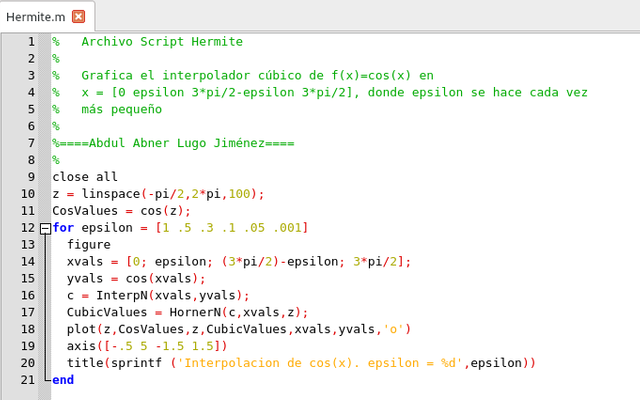
Script para la interpolación cúbica de Hermite. Elaborado en GNU Octave, por @abdulmath.
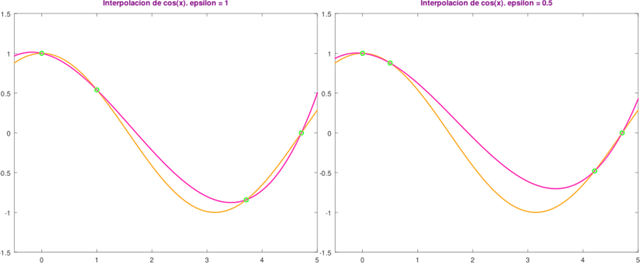
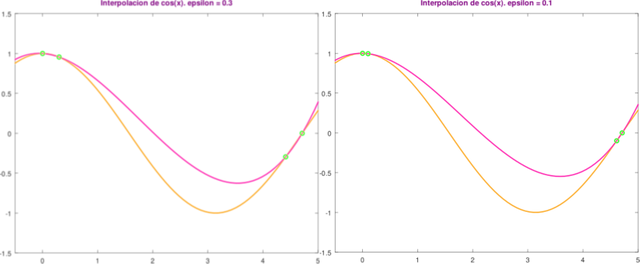
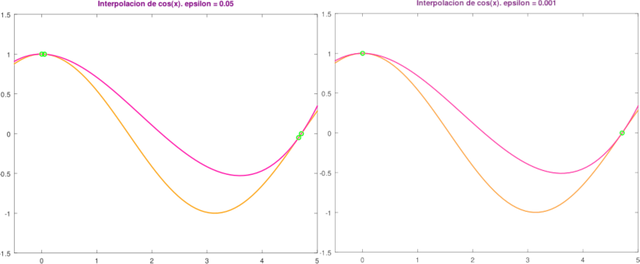
Gráficas de la interpolación cúbica de Hermite. Elaborado en GNU Octave, por @abdulmath.
A medida que los puntos se fusionan, el polinomio cúbico converge hacia un interpolador cúbico del coseno y su derivada en los puntos z = x0 y z = x4. Esto se denomina interpolador cúbico de Hermite.
En el problema de interpolación cúbica general de Hermite, se nos dan los valores de la función yL e yR, los valores de las derivadas sL y sR, y buscamos los coeficientes a, b, c y d, de modo que si

entonces
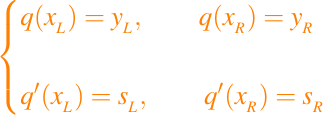
Cada una de estas ecuaciones nos dice algo sobre los coeficientes desconocidos. Notemos que

vemos que
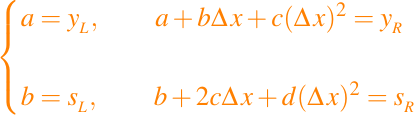
donde

Si lo expresamos en forma matricial obtenemos
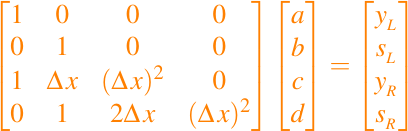
La solución a este sistema triangular es simple:
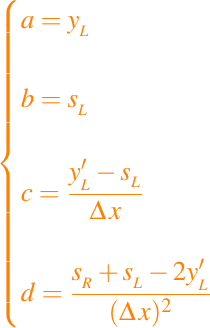
donde
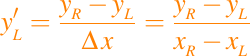
Por lo tanto podemos construir la siguiente función
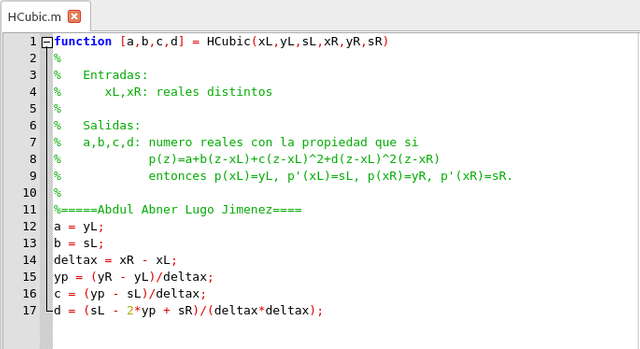
Función para hallar los coeficientes del interpolador cúbico. Elaborado en GNU Octave, por @abdulmath.
Una expresión de error para el interpolador cúbico de Hermite se puede obtener del siguiente Teorema.
Teorema 1
Supongamos que f(z) y la primera derivada de f son conitnuas en el intervalor [xL, xR] y la constantes M4 satisface

para todo valor de z en el intervalo [xL, xR], si q es el interpolador cúbico de Hermite de f en xL y xR, entonces
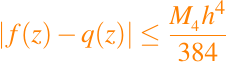
donde h = xR - xL.
El teorema lo que nos indica que si la longitud del intervalo se divide por 10, entonces la cota del error se reduce por un factor de 104.

Representación y Configuración
Ahora mostraremos cómo unir una sucesión de interpolantes cúbicos de Hermite para que el polinomio cúbico resultante C(z) interpole los datos (x1, y1t), . . . , (xn, yn), con las pendientes establecidas s1, s2, . . . , sn. Para ese fin asumimos x1 < x2 < . . . < xn y definimos el i-ésimo polinomio cúbico local por
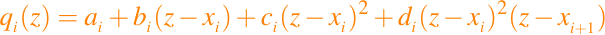
Definimos el polinomio cúbico a trozos por
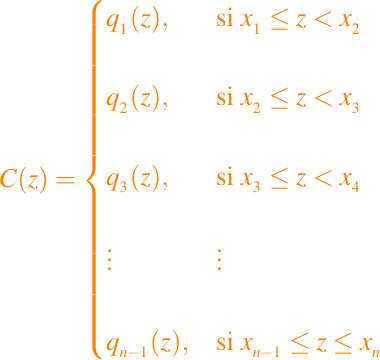
Nuestro objetivo es determinar a(1: n-1), b(1: n-1), c(1: n-1), y d(1: n-1) tal que
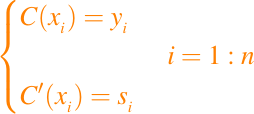
Este será el caso si simplemente resolvemos los siguientes n - 1 problemas cúbicos de Hermite:
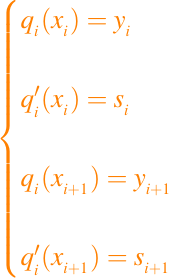
Aplicando lo que hicimos con el interpolador cúbico para cada i tenemos entonces
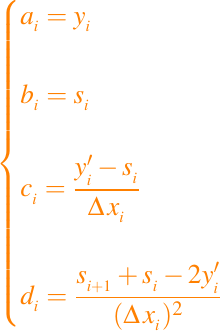
donde

y
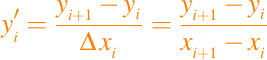
Podríamos usar
HCubic para resolver los coeficientes:
Pero obtener una mejor solución podemos vectorizar los cálculos de la siguiente manera
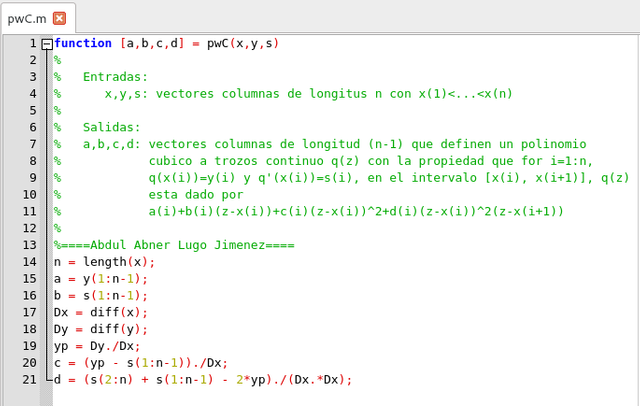
Script de la función para vectorizar los resultados de los coeficientes. Elaborado en GNU Octave, por @abdulmath.
Si M4 acota |f(4)(x)| en el intervalor [x1, xn], entonces por el Teorema anterior implica que
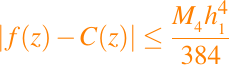
para todo valor de z en el intervalo [x1, xn], donde h1 es la longitud del subintervalo mas grande, es decir, máxi|xi + 1 - xi|.

Evaluación
La evaluación de C(z) tiene dos partes. Al igual que con cualquier polinomio por partes que deba evaluarse, se debe determinar la posición de z en la partición. Una vez que se logra esto, se debe evaluar el cúbico local correspondiente. Así, anexamos una función que se puede usar para evaluar C en un vector de valores z:
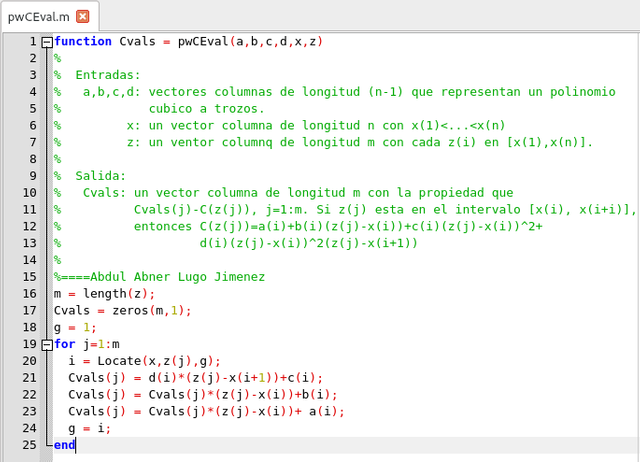
Script para Evaluar la función C(z). Elaborado en GNU Octave, por @abdulmath.
De forma análoga a
pwLeval utilizamos Locate para determinar el subintervalo que contiene a la j-ésimo punto de evaluación zj. La versión cúbica de HornerN se usa para evaluar el polinomio cúbico local apropiado. En el siguiente script mostraremos el uso de pwC y pwCEval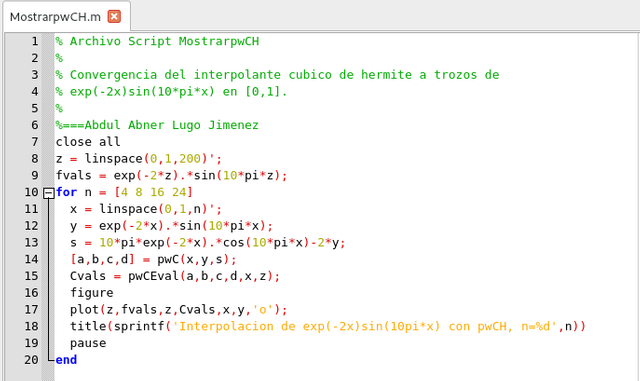
Script de evaluaciones de las funciones
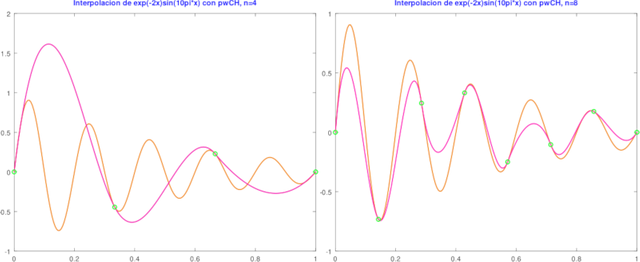
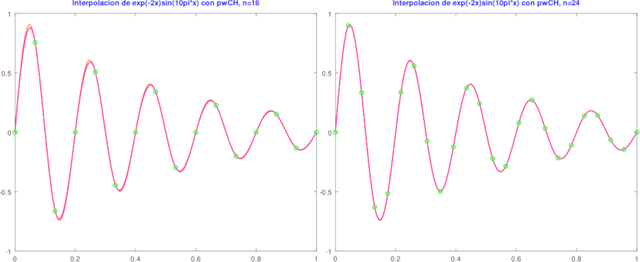
pwC y pwCEval. Elaborado en GNU Octave, por @abdulmath.A continuación mostramos la figuras generadas por el script anterior, donde podemos apreciar, que a medida que incerementamos el numero de puntos sobre la partición, el interpolante cúbico de Hermite converge a la función f.

Queridos amigos y lectores, espero hayan disfrutado y aprendido un poco más sobre la Interpolación Polinomial a Trozos usando el entorno GNU Octave, (1era Parte y 2da Parte) donde pueden usar las funciones construidas y usar los script de aplicaciones modificandolos con nuevas funciones y así poner en práctica todo lo que hemos aprendido hasta el momento. Estoy seguro que será de mucho apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
- Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
- Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

Imagen diseñada con GIMP y elaborada por @abdulmath.

This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Thanks for the support
Hi @abdulmath!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks for the support
Muy buen trabajo amigo @abdulmath. Debido a su excelente presentación y a su muy buen contenido, disfruté leerlo. Si tienes algún tiempo disponible, te invito a ver mi post sobre la Energía. Saludos.
Hola amigo @tsoldovieri, agradecido por tus buenas comentarios, y mucho mas que la lectura haya sido provechosa y te gustará mucho. con gusto pasaré por tu blog. Saludos.