Integración Numérica con GNU Octave | 1era Parte


Introducción
Una regla de cuadratura Q de m puntos para la integral definida
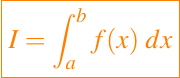
es una aproximación de la forma
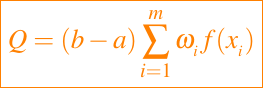
donde xi son las abscisas y wi son los pesos. Las abscisas y los pesos definen la regla y se eligen de modo que Q sea aproximadamente igual a I. La eficiencia depende esencialmente del número de evaluaciones de la función. Esto se debe a que el tiempo necesario para evaluar f en xi suele ser mucho mayor que el tiempo necesario para formar la combinación lineal requerida de valores de función. Por lo tanto, una regla de seis puntos es el doble de costosa que una regla de tres puntos.
Comenzaremos con la familia de reglas de cuadraturas de Newton-Cotes. Estas reglas se obtienen mediante la integración de un interpolador polinómico del integrando f(x). Posteriormente, discutiremos reglas compuestas basadas en una partición del intervalo [a, b] en subintervalos. En una regla compuesta, se aplica una regla simple a cada subintegral y posteriormente se suma el resultado. Se enfatiza la determinación adaptativa de la partición con control del error y conduce a una clase importante de procedimientos de cuadratura que se adaptan al comportamiento del integrando. El problema de cuadratura es ideal para introducir algunas de las ideas clave asociadas con la computación paralela.

Las Reglas de Newton-Cotes
Una forma de obtener una regla de cuadratura Q es integrar una aproximación polinomial p(x) del integrando f(x). La filosofía podemos resumirla como sigue
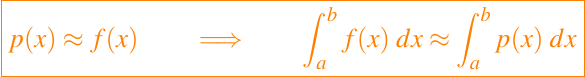
Las reglas de cuadratura de Newton-Cotes se obtienen integrando interpolaciones polinomiales del integrando espaciadas uniformemente.
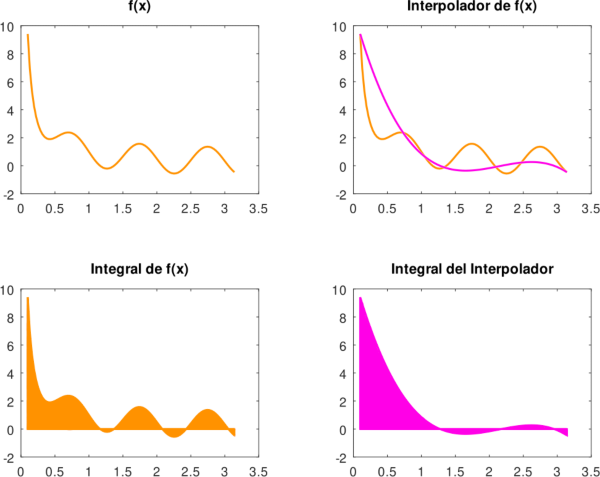
Gráficas que la función y su interpolante, así como de sus respectivas integrales. Elaboradas en GNU Octave, por @abdulmath.
La regla de Newton-Cotes de m puntos, para valores de m mayores o iguales a 2, está definida por

donde pm -1(x) interpola a f(x) con
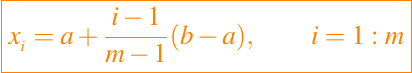
Si m = 2, entonces obtenemos la regla del trapezoide, dada por
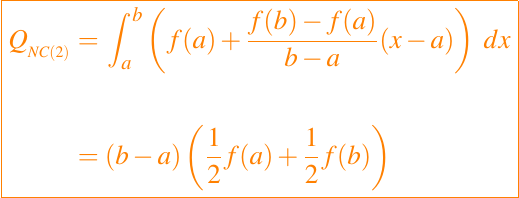
Si m = 3 y c=(a + b)/2 entonces obtenemos la regla de Simpson, dada por
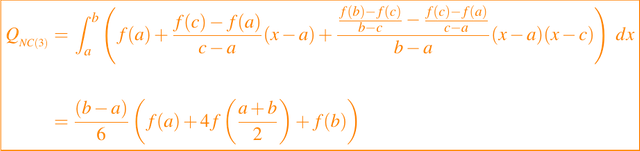
A partir de estos ejemplos de bajo grado, parece que se obtiene una combinación lineal de evaluaciones f al expandir el lado derecho de la ecuación dada en (1).

Derivación
Para el caso general de m puntos, procedemos sustituyendo la representación de Newton
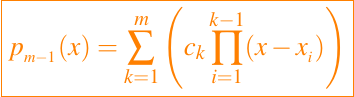
en la ecuación (1) obteniedo lo siguiente:
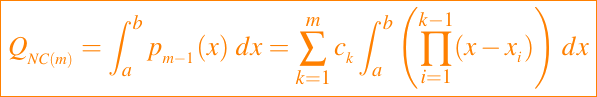
Si establecemos x = a + sh, donde h = (b - a)/(m - 1), entonces obtenemos la siguiente ecuación
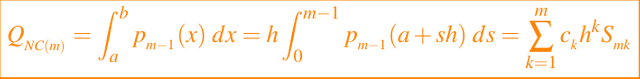
donde
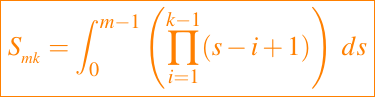
Los términos ck son diferencias divididas. Debido que están igualmente espaciados, ellos tienen una forma particularmente simple en términos de fi, como ya lo vimos en Interpolación Polinomial usando el entorno GNU Octave | 3ra Parte. Por ejemplo,
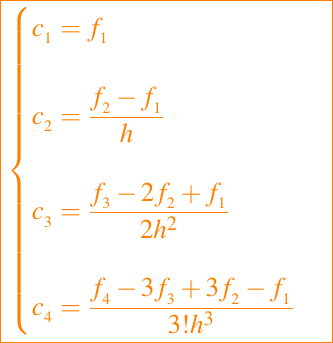
Fórmulas para Smk también pueden ser obtenidas. Aquí mostramos algunos ejemplos:
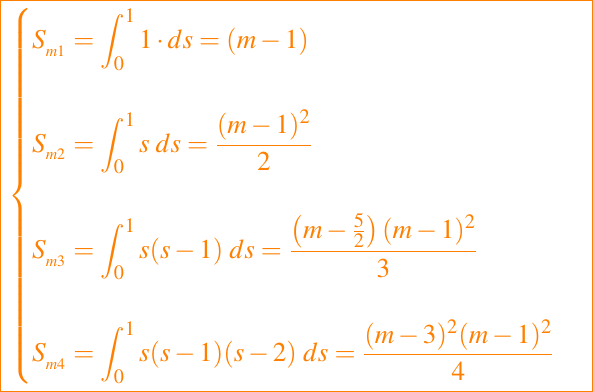
Usando estas tabulaciones podemos derivar fácilmente los pesos para cualquier regla particular de m puntos. Por ejemplo, si m = 4, entonces tenemos

Así
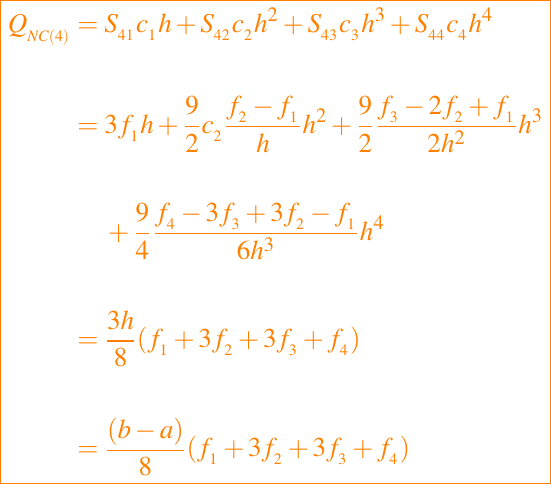
mostrando que

son el vector de pesos para QNC(4).

Implementación
Por conveniencia para cálculos posteriores, empaquetamos en una función los vectores de pesos de Newton-Cotes para algunas reglas:
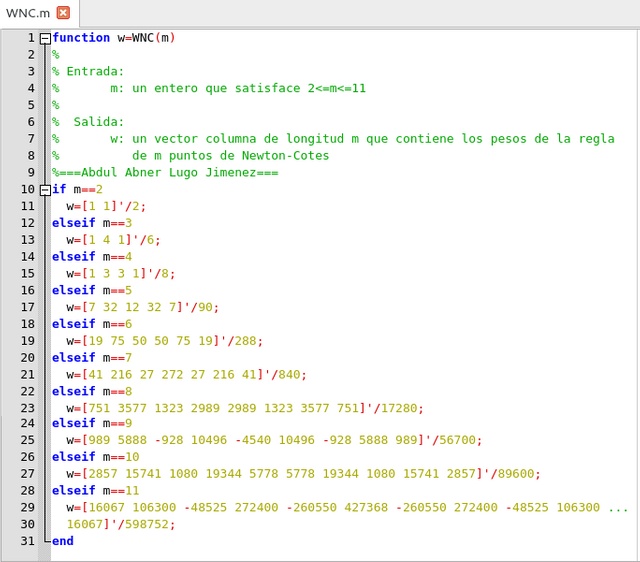
Función para suministrar los vectores de pesos desde m = 2 hasta m = 11. Elaborado con GNU Octave, por @abdulmath.
Observe que los vectores de pesos son simétricos con respecto a su centro en w(1: m) = w (m: -1: 1). Volviendo ahora a la evaluación de QNC(m) en sí, vemos que
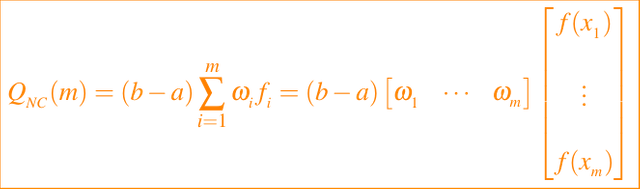
que es un producto interno escalar del vector de peso y el vector de valores de función. Por lo tanto, obtenemos la siguiente función:
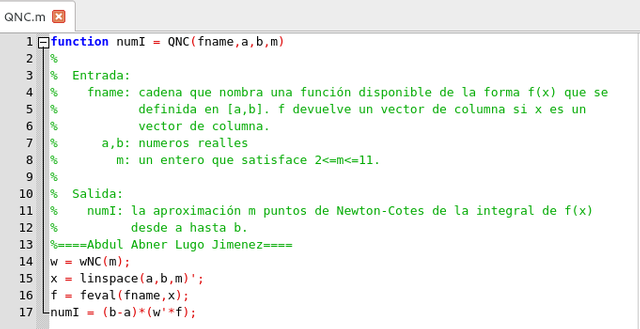
Función que da como salida la aproximación de la cuadratura de Newton-Cotes para puntos desde m = 2 hasta m = 11. Elaborado con GNU Octave, por @abdulmath.
El siguiente Script sirve para la experimentación con esta función:
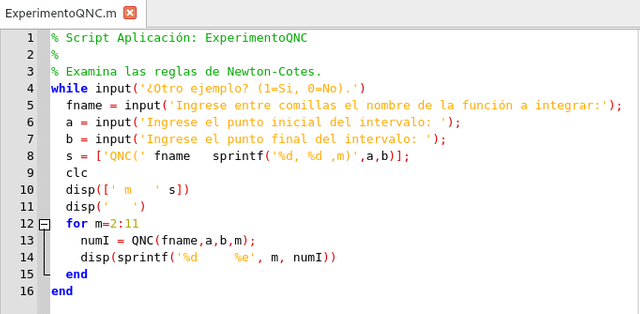
Script de Aplicación de la función
QNC y wNC. Elaborado en GNU Octave, por @abdulmath.Para la integral de la función seno desde 0 hasta pi/2, del script anterior obtenemos:
| m | QNC('sin' 0, pi/2, m) |
|---|---|
| 2 | 0.7853981633974483 |
| 3 | 1.0022798774922104 |
| 4 | 1.0010049233142790 |
| 5 | 0.9999915654729927 |
| 6 | 0.9999952613861667 |
| 7 | 1.0000000258372355 |
| 8 | 1.0000000158229039 |
| 9 | 0.9999999999408976 |
| 10 | 0.9999999999621675 |
| 11 | 1.0000000000001021 |

Error Newton-Cotes
¿Qué tan buenas son las reglas de Newton-Cotes? Como se basan en la integración de un polinomio interpolante, la respuesta depende claramente de la calidad del interpolante. Aquí mostraremos un resultado para la regla de Simpson:
Teorema 1
Si f(x) y sus primeras cuatro derivadas son continuas en [a, b], entonces
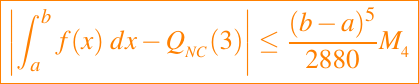
donde M4 es una cota superior de |f(4)(x)| en [a, b].
Notemos que si f(x) es un polinomio cúbico, entonces f(4) = 0 y entonces la regla de Simpson es exacta. Esto es algo sorprendente porque la regla se basa en la integración de un interpolador cuadrático. En general, se puede demostrar que

donde cm es una constante pequeña, eta esta en el intervalo [a, b], and
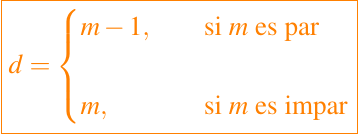
Observe que si m es impar, como en la regla de Simpson, entonces se obtiene un grado extra de precisión.
De (2), vemos que se requiere conocer f(d + 1) es requerido para decir algo sobre el error en QNC(m). Por ejemplo, si
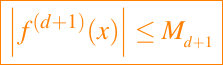
en [a, b], entonces
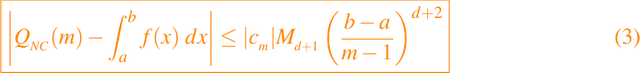
La siguiente función se puede usar para devolver esta cota superior dado el intervalo [a, b], m, y la apropiada cota de la derivada:
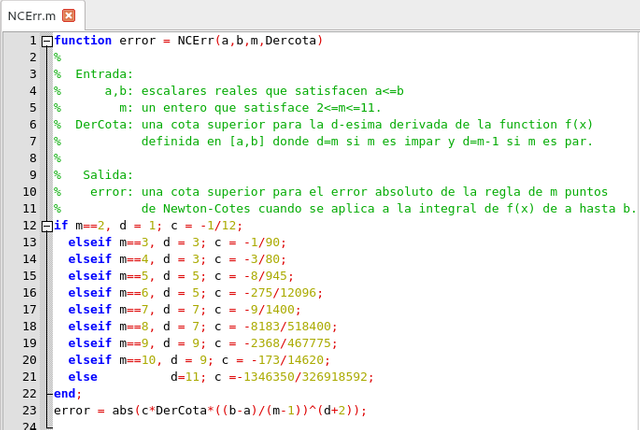
Función que calcula la cota superior. Elaborado con GNU Octave, por @abdulmath.
De esto vemos que si está contemplando una regla m par, entonces la regla de (m - 1) puntos es probablemente igual de buena y requiere una evaluación menos de la función. El siguiente script ilustra este punto:
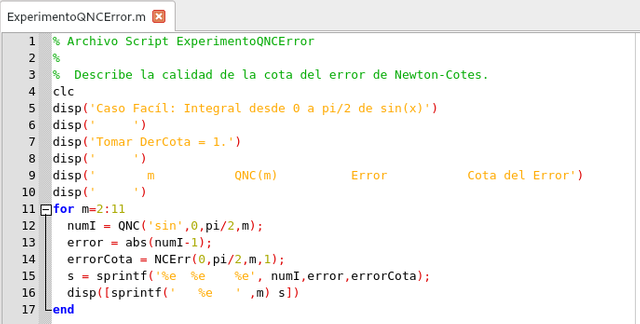
Script de Aplicación. Elaborado con GNU Octave, por @abdulmath.
Los resultados los podemos resumir en la siguiente tabla
| m | QNC(m) | Error | Cota del Error |
|---|---|---|---|
| 2 | 0.7853981633974483 | 2.146e-01 | 3.230e-01 |
| 3 | 1.0022798774922104 | 2.280e-03 | 3.321e-03 |
| 4 | 1.0010049233142790 | 1.005e-03 | 1.476e-03 |
| 5 | 0.9999915654729927 | 8.435e-06 | 1.219e-05 |
| 6 | 0.9999952613861667 | 4.739e-06 | 6.867e-06 |
| 7 | 1.0000000258372355 | 2.584e-08 | 3.714e-08 |
| 8 | 1.0000000158229039 | 1.582e-08 | 2.277e-08 |
| 9 | 0.9999999999408976 | 5.910e-11 | 8.466e-11 |
| 10 | 0.9999999999621675 | 3.783e-11 | 5.417e-11 |
| 11 | 1.0000000000001021 | 1.021e-13 | 1.460e-13 |

Una Nota de Reglas Abiertas
Las reglas de Newton-Cotes presentadas previamente son en realidad las reglas de Newton-Cotes cerradas porque f(x) se evalúa en los puntos finales izquierdo y derecho. La regla de Newton-Cotes abiertas de m puntos coloca las abscisas en a + (i - (1/2))h, donde h = (b - a)/m y i = 1: m. Las abcisas para las reglas de cuatro puntos cerradas y abiertas se muestran en la figura anexa.

Colocación de abscisas de cuatro puntos de Newton-Cotes
La regla de Newton-Cotes abierta de un punto es llamada regla de punto medio. Para m = 3, 5, 6,7, . . . las reglas abiertas implican pesos negativos, una característica que puede socavar la estabilidad numérica de la regla. (La cancelación numérica puede ocurrir con integrantes positivos, y esto puede poner en peligro el error relativo). Las fórmulas de Newton cerradas no "se vuelven negativas" hasta que m = 9, lo que las hace una familia más atractiva de reglas de cuadratura.

Queridos amigos y lectores, espero hayan disfrutado y aprendido un poco más sobre la Integración Numérica usando el entorno GNU Octave | 1era Parte donde pudimos aprender las ventajas de la integración numérica y como estimar el error cuando usamos este tipo de aproximaciones, también los invito a usar los script que les dejo y modificar las funciones dadas en los mismos y así poner en práctica todo lo que hemos aprendido hasta el momento. Estoy seguro que será de mucho apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
- Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
- Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.
Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, GNU Octave,  , GIMP e Inkscape.
, GIMP e Inkscape.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

Imagen diseñada con GIMP y elaborada por @abdulmath.
Tu constancia inspira a otros para mejorar en esta plataforma. Siempre compartes temas nuevos, donde presentas con detalle el desarrollo de tus temas. Además cuidas todos los aspectos de maquetado y diseño de tus publicaciones. Continúo aprendiendo y te dejo mis mejores deseos.
Buena vibra.
Muy agradecido por tus bonitas palabras. Trabajando, aunque a veces algunas personas menosprecian el trabajo de los demás. Adelante. Besos y abrazos.
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @abdulmath!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by abdulmath from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.