Eutrofización: Una aplicación de modelos continuos de población en un Lago.

Esta publicación esta dirigida a estudiantes, profesionales e investigadores en específico en el área de las ciencias Biológicas, o Matemáticas, y al público interesado en estos temas interesantes para el entendimiento de parte del medio que nos envuelve en el día a día. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.


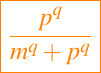
Un equilibrio para la ecuación dada en (1) es una intersección de la curva

representando la entrada de fósforo y la línea

que representa la salida de fósforo.
Debido a que la línea dada en (3) comienza en cero cuando p = 0 y es acotada mientras que la curva dada por la ecuación en (2) tiene un valor no negativo L cuando p = 0 y está acotada cuando p tiende a ∞, hay al menos un equilibrio. Pueden existir hasta tres equilibrios.
Una situación típica es la de un valor pequeño de L y un equilibrio oligotrófico; con un valor grande para L existe un equilibrio eutrófico; y con un valor intermedio de L entonces existen tres equilibrios: un equilibrio oligotrófico, un equilibrio eutrófico, y un equilibrio inestable intermedio que separa los dominios de atracción de los otros dos equilibrios.

Desde el punto de vista de la gestión de la calidad del agua, el reto es controlar el agua de un lago que se encuentra en equilibrio eutrófico y trasladarlo a un equilibrio oligotrófico. Algunas veces esto puede lograrse reduciendo la entrada de fósforo externo. Sin embargo, en algunos lagos, la reducción de los insumos externos por sí sola no puede revertir la eutrofización debido a la cantidad de reciclaje.
Para mejorar la calidad del agua de un lago de este tipo se necesitarían métodos adicionales de intervención para disminuir el reciclaje o aumentar la sedimentación. La viabilidad de estos métodos adicionales depende de las propiedades del lago.
Ahora bien, consideraremos solo lo que se puede lograr reduciendo el aporte de fósforo. En términos del modelo (1), ubicamos los equilibrios como intersecciones de la curva (2) y la línea (3). La disminución de la entrada externa de fósforo corresponde al desplazamiento de la curva (2) hacia abajo. En la figura siguiente mostramos que hay un equilibrio eutrófico para valores de L suficientemente grandes y un equilibrio oligotrófico para valores de L suficientemente pequeños, mientras que para valores de L intermedios están presentes ambos equilibrios.
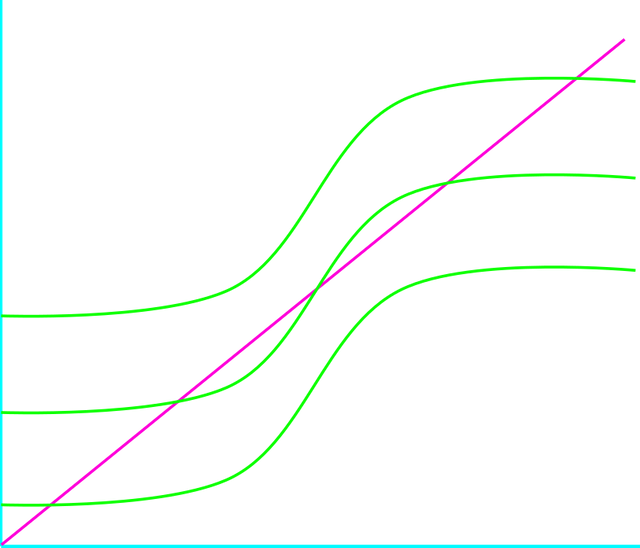
Elaborada con Inkscape, por @abdulmath.
Con el fin de gestionar el lago al equilibrio oligotrófico cuando están presentes los equilibrios oligotróficos y eutróficos, es necesario bajar la concentración de fósforo por debajo del equilibrio inestable. Esto puede requerir métodos de intervención adicionales. En la Figura siguiente existe un nivel de entrada para el cual los equilibrios eutróficos e inestables se fusionan y para el cual la línea y la curva son tangentes.
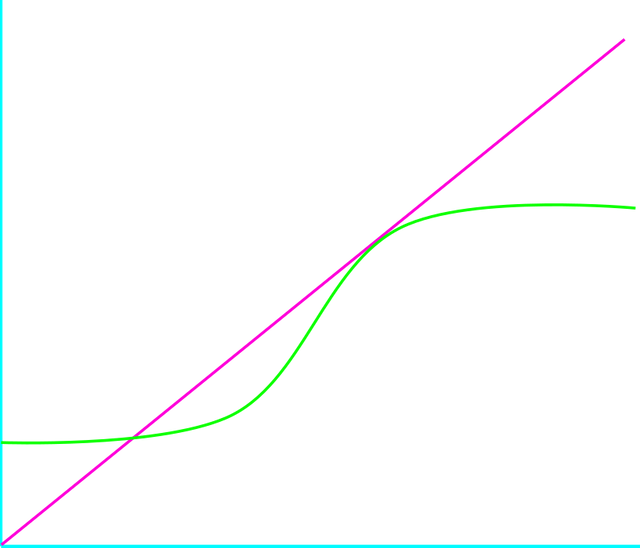
Elaborada con Inkscape, por @abdulmath.
Cuando L se reduce por debajo de este nivel crítico, solo queda el equilibrio oligotrófico. El equilibrio salta a este nivel y la eutrofización del lago se invierte. Este salto de equilibrio se conoce como histéresis, y se dice que un lago que muestra esta propiedad es histerético.
El aporte mínimo de fósforo a un lago está determinado por factores como la química del suelo, y este aporte mínimo puede no ser lo suficientemente bajo como para sacar a un lago histerético de su equilibrio eutrófico. Incluso si un lago histerético pudiera ser trasladado al equilibrio oligotrófico, los cambios en las condiciones pueden aumentar el aporte mínimo de fósforo alcanzable y conducir a la eutrofización.
Un lago histerético que se encuentra en su equilibrio oligotrópico, si es perturbado por una gran cantidad de fósforo, puede ser movido a un estado que está en el dominio de la atracción del equilibrio eutrófico. Por lo tanto, puede pasar rápidamente de un estado oligotrófico a un estado eutrófico, y este cambio puede ser bastante difícil para retroceder. Los cambios repentinos en el estado de un ecosistema pueden tener consecuencias graves. Un ejemplo muy estudiado es el colapso de una pesca debido a un cambio que no parece influir en la pesca.
Si la pendiente de la recta dada en (3) es mayor que la pendiente máxima de la curva (2) el sistema (1) tiene solo un equilibrio oligotrófico, como podemos apreciar en la figura siguiente.
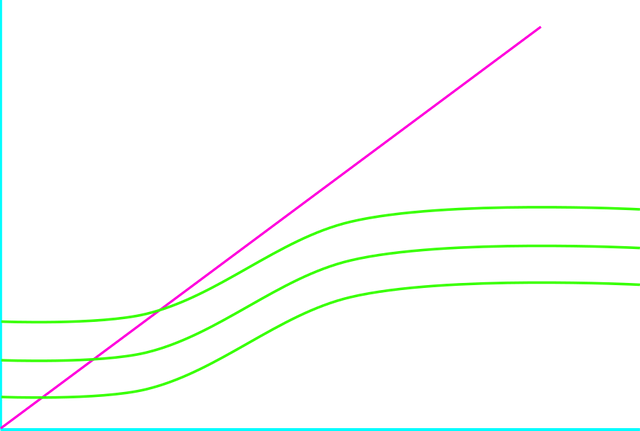
Elaborada con Inkscape, por @abdulmath.
En este caso el lago resiste la eutrofización, y un gran aporte de el fósforo puede ser absorbido sin causar daños significativos. Se dice que un lago así para ser reversible.
Por otro lado, es posible que incluso para la mínima entrada posible de fósforo la línea dada en (3) esté por debajo de la curva dada en (2) para un valor de p pequeño, y el sistema (1) tenga solo un equilibrio eutrófico, como lo podemos apreciar en la figura siguiente.
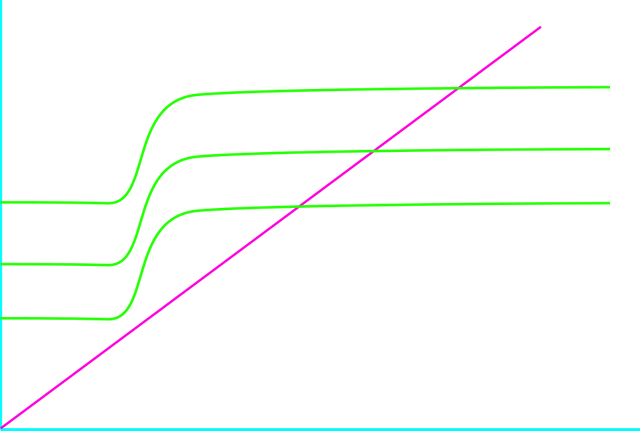
Elaborada con Inkscape, por @abdulmath.
Se dice que este lago es irreversible; es decir, no es posible llevarlo a un equilibrio oligotrófico reduciendo el aporte de fósforo.
A grandes rasgos, un lago es reversible si la pendiente s de la línea dada en (3), que representa la tasa de pérdida de fósforo, es suficientemente grande. Si s es un valor suficientemente pequeño, el lago es irreversible, y para valores intermedios de s corresponden a lagos histeréticos. La clasificación de un lago dependería tanto del valor de s como del aporte mínimo alcanzable L.

- Actividades como la agricultura, la silvicultura y el desarrollo urbano que producen un exceso de nutrientes en un lago y conducen a la eutrofización y tienen beneficios económicos directos.
- Existe una compensación entre estos beneficios y el costo de los daños al lago.
- Los distintos grupos interesados, entre los que se incluyen a los agricultores, silvicultores, promotores y activistas medioambientales, es probable que tienen diferentes estimaciones de las ganancias y pérdidas globales de una actividad.
- Para cada estimación se podría formular un modelo de optimización económica, pero también hay cuestiones políticas implicadas en la decisión de qué modelo se va a utilizar.
- Como en cualquier cuestión política, existen oportunidades sustanciales para malentendido o mala interpretación de modelos y datos.
- A modo de reflexión, el lago de valencia es un digno caso de estudio, donde se podrían desarrollar e implementar este tipo de modelos de forma experimental e irlos alimentando con datos y generar modelos mucho más complejos, con el fin determinar si es un lago irreversible o reversible según sea el caso de influencia sobre el mismo.
Queridos amigos y lectores, espero hayan disfrutar de una nueva publicación donde las matemáticas tienen sus aplicaciones en otros campos de la ciencia los cuales son de mucho interés en general. Espero que la misma haya sido de su agrado, y pueda servir de una ventana de apoyo para visualizar las estrechas relaciones que existen en particular entre las ciencias, así como se puede contextualizar las mismas teorías en las ciencias sociales, gracias por tomar un poco de su tiempo y poder disfrutar un poco más del maravilloso mundo de las matemáticas y las ciencias básicas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Clark, C. W. Mathematical Bioeconomics: The Optimal Management of Renewable Resources, 2nd ed., Wiley, New York. 1990
- Edelstein-Keshet, L. Mathematical Models in Biology, Random House, New York. 1988
- Brauer, F. and D. A. Sanchez. Constant rate population harvesting: equilibrium and stability, Theor. Pop. Biol., 8:12-30. 1975.
- Carpenter, S. R., D. Ludwig, and W. A. Brock. Management of eutrophication for lakes subject to potentially reversible change, Ecological Applications, 9:751-771. 1999.
La imagen de fondo de la portada es una imagen de libre uso tomada de y editada con GIMP por @abdulmath. Las imágenes son todas de libre uso, tomadas de
y editadas y tratadas con GIMP. Los títulos, imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, LaTeX2e, Inkscape y GIMP.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.



This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Saludos estimado amigo @abdulmath, tu post reitera la aplicabilidad de la matemática en otras disciplinas científicas en este caso particular sobre, problemas biológicos causados principalmente por actividades antropogénicas, te comento que este enriquecimiento de minerales en los cuerpos de agua (Eutrofización) es un tema de debate constante en la comunidad científica con enfoques Agroecológicos, dónde se ha planteado el reciclaje de estos nutrientes, implementando como estrategia el cultivo de Macrófitas Acuáticas como fuente extractora, destinando a posterior la biomasa colectada como materia prima en la elaboración de fertilizantes orgánicos. Tu artículo invita incluso a plantear investigaciones dónde se pueda estimar las Descargas (entrada de elementos minerales) y Extracción (salida de elementos minerales) efectuada por la acumulación de nutrientes en los orgános vegetativos de las especies acuáticas.
Saludos, sigamos creciendo.
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by abdulmath from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Has recivido un voto por @cultivandojuntos, Un voto hecho por un bot de construccion experimental en la comunidad de la etiqueta español
Hi @abdulmath!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Excelente propuesta científica y educativa @abdulmath, fijate me abriste una idea. Hace 6 años dí clases en la Universidad Bolivariana en el programa de Gestión ambiental, los alumnos en su pensum de estudio no tienen ninguna materia relacionado con matemática, con tu artículo veo una correlación de una ecuación diferencial que predice la concentración de fósforo que puede contener un lago, lo que me lleva a pensar que sería importante hacer hincapié que las universidades que tienen dentro de sus programas de formación la licenciatura en Gestión ambiental pueden añadir en su pensum las materias de cálculo, donde se puedan dar estas aplicaciones mediante el cálculo diferencial, e inclusive este tipo de profesionales puedan realizar estimaciones de contaminación de un ecosistema tan importante como un Lago, imaginate que se pueda aplicar para nuestro Lago de Maracaibo, sería buenísimo, ya que en parte el mismo se encuentra afectado por la contaminación de los derrames de hidrocarburos. Sin más que agradecido de que puedas compartir este artículo con nosotros. Saludos.