Ecuación de Difusión | Problema de Stefan

Esta publicación esta dirigida a estudiantes, profesionales e investigadores en específico en el área de las Matemáticas Aplicadas e Ingeniería, y público interesado en estos temas interesantes para el entendimiento de buena parte del medio que nos rodea día a día. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.


Si el cambio de fase entre un sólido y un líquido ocurre en un plano en movimiento dado por x = s(t), con el sólido en x < s(t) como lo podemos apreciar en la figura siguiente,
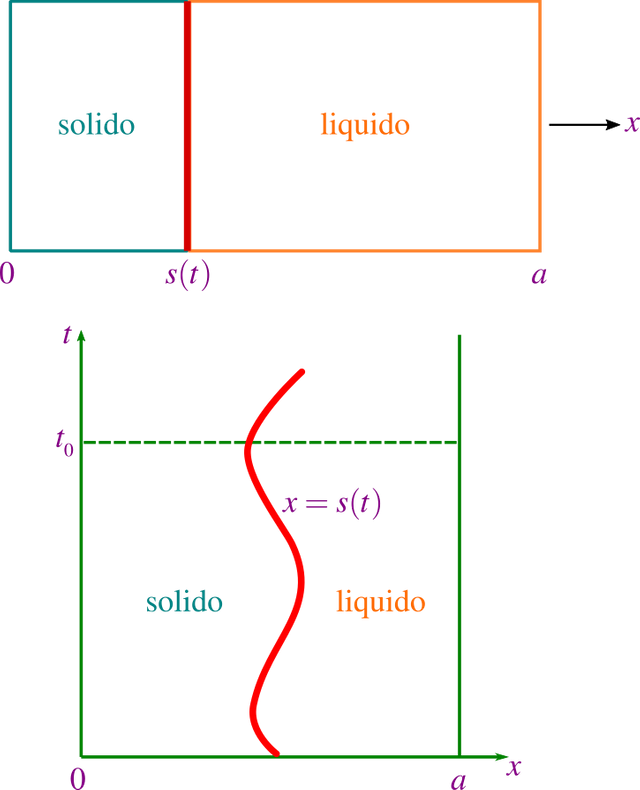
Dominio de un problema de Stefam. Elaborado por @abdulmath.
entonces las condiciones en la frontera son que la temperatura tanto en la fase sólida como en la fase líquida es la temperatura de fusión Tm, y un balance energético dado por la condición de Stefan
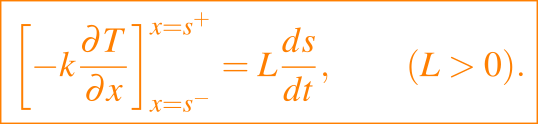
La masa también debe conservarse, y si las densidades de las dos fases son las mismas, lo que es una suposición razonable para la interfaz sólido/líquido pero no para la interfaz líquido/gas, entonces no hay movimiento relativo de las dos fases. Con el sólido en reposo y las diferentes densidades, la velocidad del fluido esta dada por
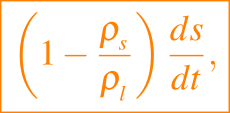
al aplicar un balance de masa. También se debe conservar el momento, y el balance de momento es necesario para determinar la tensión ejercida por el fluido en el sólido.
Sin movimiento de fluido, T satisface
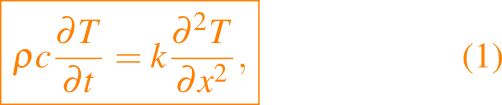
en ambas fases, y por simplicidad asumiremos que ρ, c y k son constantes con los mismos valores en cada fase. Luego la ecuación (1) y la condición de Stefan, junto con las condiciones de fronteras usuales para un problema parabólico, completan el problema de Stefan:
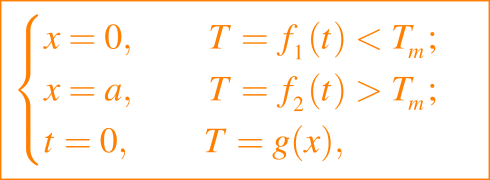
donde
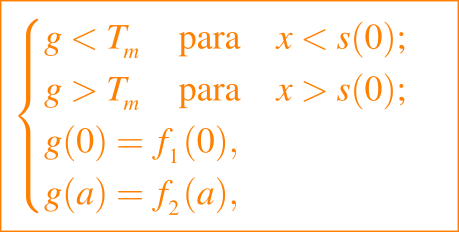
Esto se interpreta fácilmente como un problema físico sensible, y las dos fases se muestran la gráfica del dominio del problema de Stefan x vs. t.
Si la fase fluida está bien agitada, o tiene un movimiento turbulento de modo que, al mezclarse, su temperatura es uniforme e igual a la temperatura de fusión, entonces se dice que el sólido es ablating. Para un bloque sólido unidimensional, la temperatura satisface ecuación dada en (1) junto con las condiciones de frontera en x = s(t), que son:
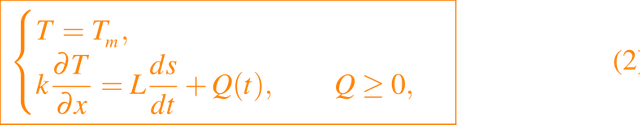
donde Q es la entrada de calor en la frontera de cambio de fase. Esto, junto con las condiciones de frontera dadas por
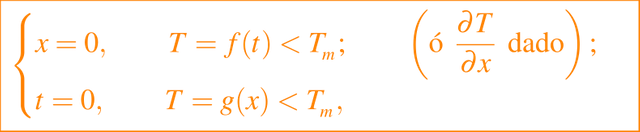
donde

es un problema de Stefan en una fase. Rubinstein (1971) muestra una discusión detallada de algunos problemas bien planteados de una simple fase y dos fases, pero para los tipos de problemas de Stefan no hay un resultado general de problemas bien planteados y no es difícil construir problemas mal planteados.
La solución exacta más simple es que una superficie plana de cambio de fase se mueva con velocidad constante U hacia un fluido a la temperatura de fusión. Luego hay una solución dada en (1) es de la forma siguiente:

que satisface T = Tm en x = Ut.
De la condición Stefan, tenemos que A = L/ρc y para U > 0, T < Tm en el sólido. Para U < 0, en caso de que surja tal situación, entonces T > Tm en la fase sólida y se dice que el sólido está sobrecalentado.
Una solución bifásica con frontera de cambio de fase que se mueve a velocidad constante tiene la misma forma de la ecuación dada en (3), excepto que A se sustituye por As en x < Ut y por Ajl en x > Ut, donde As - Al = L/ρc. Cuando U > 0 es posible tener una nueva situación, es decir, As = 0, Al < 0, cuando el fluido está sobreenfriado.
Para un problema bien planteado, es necesario que la frontera de cambio de fase sea estable a pequeñas perturbaciones, y examinamos la estabilidad del problema de frontera plana en movimiento de una fase prescribiendo una pequeña perturbación periódica en la dirección y normal al movimiento de la frontera. Primero se debe obtener la condición de Stefan
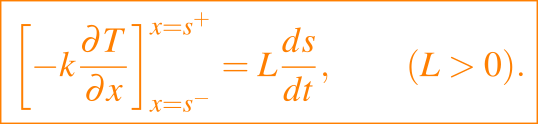
para una frontera no plana definida por F(x, t) = 0. Si la dirección normal de la superficie hacia el fluido es n, entonces un balance de energía proporciona

la cual podemos escribir de la forma
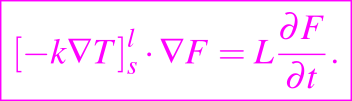
Cuando F = x - s(t) esto reduce a la condición de Stefan, y para F = x-s(t, y) y T = Tm en el líquido, se reduce a
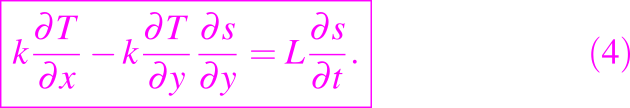
Para una superficie de cambio de fase
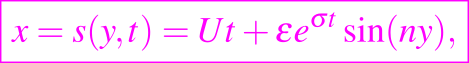
donde ε << 1 y n > 0, buscamos una distribución de temperatura
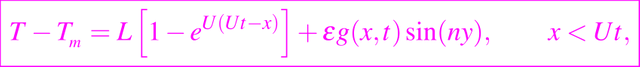
donde para facilitar la manipulación las variables han sido escaladas de manera que k = ρc = 1.
Ahora T satisface la ecuación de conducción de calor bidimensional, de modo que
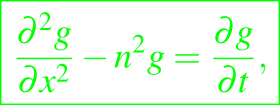
que tiene soluciones de la forma

si m2 - n2 = σ - mU, y si m > -U las perturbaciones permanecerán pequeñas comparadas con las soluciones no perturbadas para (Ut - x) grandes. La condición T = Tm implica que en x = Ut,

para que LU+a = 0. La condición Stefan de la ecuación dada en (4) implica que en x = Ut,
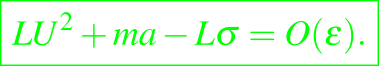
Eliminando a y sustituyendo σ, obtenemos (m + U)2 = n2. Con una raíz positiva m + U = n se cumple la condición para Ut - x y σ = -Un.
La superficie plana de cambio de fase es por lo tanto estable a pequeñas perturbaciones si U > 0 cuando el sólido no está sobrecalentado. Con U < 0 y el sólido sobrecalentado la frontera es inestable, y el problema de Stefan está mal planteado. Esta condición de estabilidad, que implica que la frontera libre sólo es estable si la fase sólida se convierte en una región de temperatura constante y no viceversa, es directamente análoga a la estabilidad de la frontera fluida en una celda Hele-Shaw. El problema Hele-Shaw es, sin embargo, más fácil ya que p satisface la ecuación de Laplace y no la ecuación de difusión bidimensional. El resultado es que la frontra sólo se mueve establemente en la dirección de disminución de la presión es sin embargo idéntico.



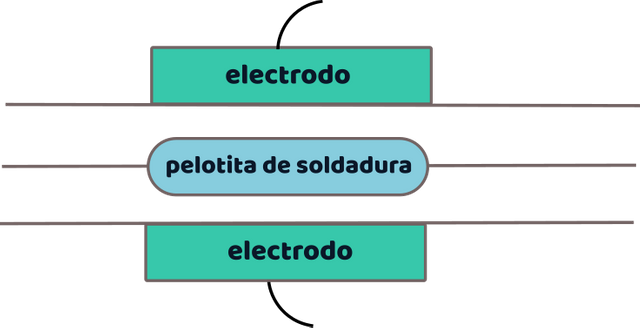
Modelo de soldadura en dos placas de acero. Elaborado por @abdulmath.
La temperatura T satisface la ecuación de conducción de calor con un término fuente Q = RI2, donde R es la resistencia local que puede depender de la temperatura e I es la magnitud de la corriente local. Sin embargo, si se utiliza una corriente alterna y los electrodos tienen una gran inductancia constante, la amplitud de la corriente es esencialmente constante. Además, la escala de tiempo del proceso de soldadura es mucho más largo que el tiempo del ciclo de corriente alterna, de modo que el valor cuadrado medio de la corriente proporciona la fuente de calor y puede ser tomado como constante. Para el acero dulce por debajo de unos 400 °C, la resistencia aumenta con la temperatura, pero por encima de 400 °C se mantiene aproximadamente constante. Por lo tanto, habrá un problema inicial en el que el metal se calentará rápidamente hasta los 400 °C debido al creciente término fuente; también los transitorios de corriente y la resistencia del aire entre las placas, y los electrodos y las placas, complicarán este problema inicial. El interesante rango de temperatura está por encima de los 400 °C, y se modelará el problema con una temperatura inicial que está por encima de los 400 °C y asumiremos que el tiempo que se tarda en alcanzar este estado es pequeño y puede ser estimado. Es probable que las conductividades térmicas en las fases de fusión y sólida sean muy diferentes, pero para simplificar el análisis haremos caso omiso de ello, aunque podría incorporarse de forma directa.
Con variables no dimensionales tales que las placas son de espesor 1, la difusividad es 1, y
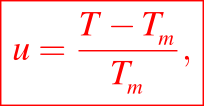
entonces u satisface

donde
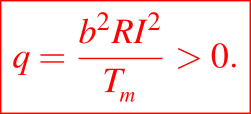
Por simetría la derivada parcial de u con respecto a x en x = 0 donde las placas se tocan; e inicialmente en t = 0, u = g(x)<0. En x = 1, la cara de la placa que toca un electrodo, la condición de frontera será la continuidad de la temperatura y el flujo de calor hacia el electrodo. Para evitar tener que analizar la distribución de la temperatura en el electrodo, se determina un coeficiente empírico de transferencia de calor H. Esto nos da la condición de frontera
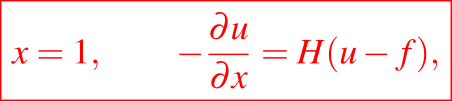
donde f es la temperatura media del electrodo. Para completar el problema se requiere una condición en la frontera de cambio de fase u = 0, y la condición de Stefan en estas variables es,

donde
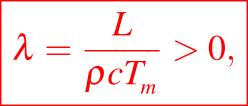
es el número de Stefan.
Este problema del valor en la frontera se puede mostrar en una gráfica x vs t como el que mostramos a continuación, pero este no está bien planteado.
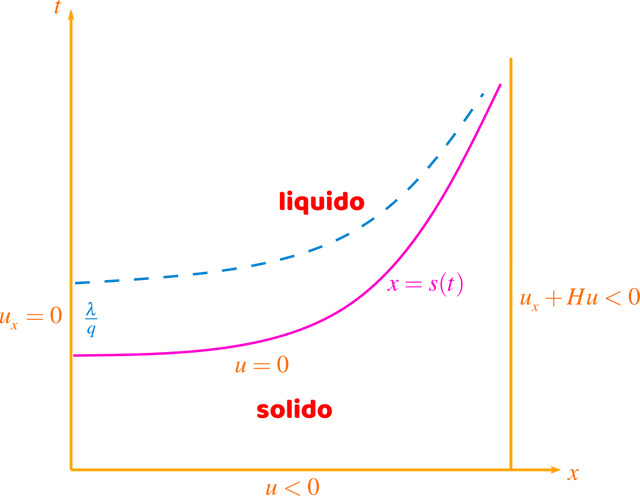
Dominio para el problema de soldadura. Elaborado por @abdulmath.
Una simple ilustración de la falta de positividad de este modelo es considerar la partícula que primero alcanza la temperatura de fusión u = 0. Será en x = 0, y para cambiar su fase tiene que adquirir una cantidad de calor λ para aumentar su entalpía o calor total. Dado que la partícula está en el punto más caliente, no puede recibir calor por conducción, y recibe calor sólo de la fuente de calor. Adquirir una cantidad de calor λ a una velocidad q tomará un tiempo λ/q y su temperatura allí permanece constante, igual a cero, durante este período de tiempo. Por lo tanto, debe existir una región de temperatura constante en el plano, en la cual el material no es totalmente sólido ni fundido, llamada región blanda. Por lo tanto, el cambio de fase no tiene lugar de forma discontinua.
Queridos amigos y lectores, espero hayan disfrutado de una nueva publicación donde las matemáticas tienen sus aplicaciones en otros campos de la ciencia los cuales son de mucho interés en general. Espero que la misma haya sido de su agrado, y pueda servir de una ventana de apoyo para visualizar las estrechas relaciones que existen en particular entre las ciencias, así como se puede contextualizar las mismas teorías en la ingeniería, gracias por tomar un poco de su tiempo y poder disfrutar un poco más del maravilloso mundo de las matemáticas y las ciencias básicas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Bender, C. M. and Orszag, S. A. Advanced mathematical methods for scientists and engineers. McGraw-Hill, New York. 1978.
- Courant, R. and Hilbert, D. Methods of mathematical physics, vol. I. Interscience, New York. 1976.
- Landau, L. D. and Lifshitz, E. M. Fluid mechanics. Pergamon, London. 1963.
- Stakgold, I. Green's functions and boundary value problems. Wiley-Interscience, New York. 1979.
- Rubinstein, L. I. The Stefan problem. American Mathematical Society, Providence. 1971.
La imagen de fondo de la portada es una imagen de libre uso tomada de Pixabay y editada con GIMP por @abdulmath. Las imágenes son todas de libre uso, tomadas de Pixabay y editadas y tratadas con GIMP. Los títulos, imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, LaTeX2e, Inkscape y GIMP.



Si te gusta nuestro contenido,ven y apoya a @Cervantes como Witness en
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by abdulmath from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Este artículo me fue más fácil de comprender... sobre todo porque se ve un ejemplo fácil en el área metalúrgica, incluso hasta en la artesanía se observa esta aplicación porque cuando diseñas dijes debes llenar moldes con el material derretido (normalmente estaño).
This post is supported by @tipU upvote :)
@tipU voting service always profitable, instant upvotes | For investors.
Admiro tu dedicación y tu trabajo para mostrar información que llevan a un aprendizaje importante. La constancia tiene buenos resultados y se nota tu crecimiento en esta gran plataforma. Sinceras felicitaciones.
Buena vibra.
Maravillosa publicación saludos mi estimado @abdulmath
Excelente colega...
Te has convertido en parte de mi problema Stefan...
jejeje...
Mi frontera del cambio de fase se desplaza en el tiempo, cambiando mi horizonte y mi estado catatónico, que se pulveriza de solido a liquido y luego se volatiliza a gaseoso, para la trascendencia de mi materia inerte y alcanzar el Espacio Sideral. Cuando nuestros puntos máximos convergen y es alcanzado por la temperatura de fusión, que hacen estallar los átomos y el calor es absorbido por tus catalizadores, en compás con tu entalpía, que la conduces en mi plano constante, donde se funde parte de la partícula sólida, transmutando el material en la llamada región blanda. Por lo tanto, el cambio de nuestras fases no tiene lugar de forma discontinua.
Jejeje...
Me diste una idea, para hacer un post con Cantos Poéticos al Amor a Través de las Matemáticas, EUREKA... Ya veo, que Stefan no solo nos mete en problemas con eso, sino que puede aplicarse también al Amor.
Excelente Artículo, Felicidades Corazón.