Maximum errors in computing volume and surface areas with Differentials
Let's have a look at a more practical example of the use differentials. One of the applications is in calculating maximum errors of volumes and surface areas of objects, given certain errors in measurement.
For instance, here is a cube with side length s = 30cm and a possible error in measurement of 0.1cm.
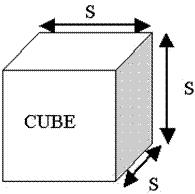
Image Source
Now, the volume of a cube with side length s is given by...
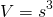
If we consider the error in measurement of the side length to be Δs = ds, then the error in calculating the volume would be ΔV, which we can approximate with the differential dV.
And hence by differentials,
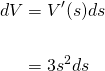
And given s = 30cm and ds = 0.1cm,
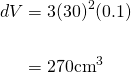
Thus the maximum possible error in calculating the volume of this cube is 270cm3, which seems huge. But remember, our cube has a side length of 30cm, which means the precise volume is...
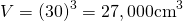
Thus the relative error is...
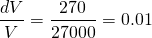
...or 1% of the total volume, which seems a lot more reasonable.
Algebraically, the relative error in calculating volume is...
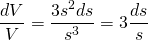
...which means we can expect the maximum error in calculating volume to be within 3 times the error in side length measurement.
Now, what about surface area? For our cube, it is given by...
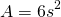
Again, we can approximate the error as dA by differentials...
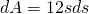
Hence the relative error in surface area calculation is...
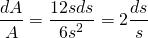
...or about 2 times the relative error in the side length measurement.
So calculating this relative error...
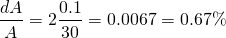
This example problem was adapted from an exercise in Calculus 5th Edition by James Stewart.
Here's a list of posts created so far on the subject of Linear Approximations and Differentials:
- Linear Approximations Part 1 - Interpolating between Empirical Data
- Linear Approximations Part 2 - Estimating values of f(x) = √(x+2) near x = 2
- Linear Approximations Part 3 - why sin(x) ≅ x near 0
- The Geometric Meaning of Differentials
- Differentials: Comparing dy and Δy for y = x^2 at x = 1 and Δx = 0.5
- Estimating (2.001)^5 with Differentials and Linear Approximations
- Maximum errors in computing volume and surface areas with Differentials
Please give me an Upvote and Resteem if you have found this tutorial helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
I would really appreciate any small donation which will help me to help more math students of the world.
Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu
Man you must be a genius in the field of mathematics. This is one the best post I have read on steeemit since I joined the community. You are really a seasoned professional and this post has helped and would still help more student of like me. More of it I enjoy such posts they make me like steemit the more. Glad to knw people like you exist here.
Wow, thank you for your kind comment @orishtimothy. No, I don't consider myself a math genius, haha. I often struggled with understanding it in my earlier University days. I think a strength of mine is once I do understand something, I'm good at educating others.
Yea that is a principle that I adopted too in my school days- teaching every thing I understood to other by so doing perfecting and learning more. All the same it really helped thanks once more
@originalworks
The @OriginalWorks bot has determined this post by @masterwu to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!