Linear Approximations Part 2 - Estimating values of f(x) = √(x+2) near x = 2

In part 1, we went over the idea of linear approximations and how it could apply to estimating values nearby to empirical, statistical or experimental data points.

In this post, let's see how accurately we can estimate expressed, continuous and differentiable functions.

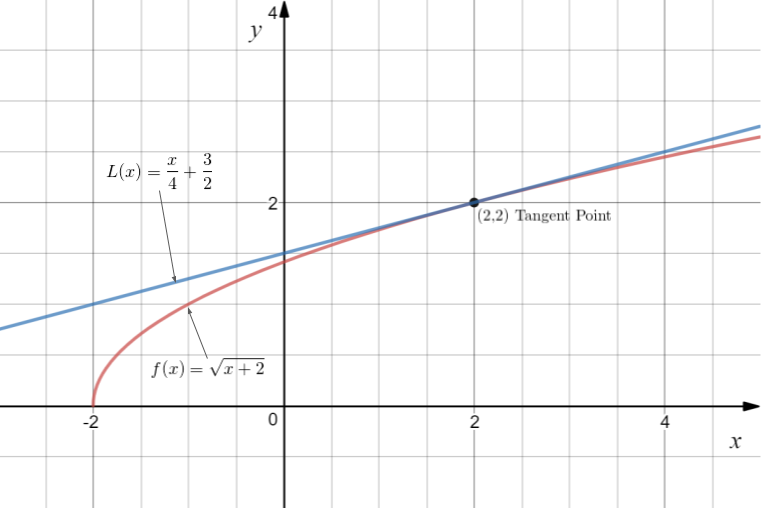Created with: www.desmos.com/calculator

For example, let's find the linearisation of...

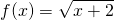
...at x = 2. Let's use this result to estimate √3.97 and √4.05.

Ok, now firstly, the derivative of the function is...

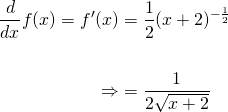
At x = 2, the derivative evaluates to....

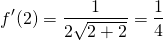
And f(2) evaluates to...

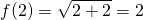
Remember the tangent line or linearization formula for L(x) is given by...

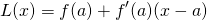
So substituting the values for f(2) and f'(2) and a = 2 gives...

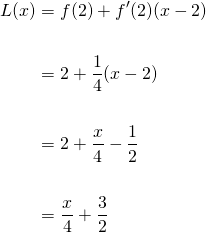
Therefore, our linear approximation of f(x) around x = 2 is...

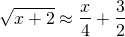
Ok, great. So now let's test this approximation to see how accurate it is for √3.97. Note, in this instance, x + 2 = 3.97, thus x = 1.97. By our linear approximation...

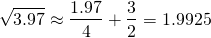
And entering √3.97 into a scientific calculator, the full display result is...

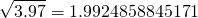
Our linear approximation is accurate to within 0.002%!

Let's try the same process with √4.05. Our approximation is...

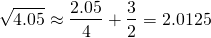
Again, checking with a scientific calculator...

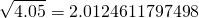
This time, our approximation is accurate to within 0.004% by virtue of x = 2.05 being a little bit further away from x = 2 compared to x = 1.97. But it's still a pretty good estimate.

The solution is graphed in the figure above. We can see that indeed, the tangent line L(x) is a good approximation for f(x) near x = 2. Note that our approximations will be over estimates, since the tangent line is above the curve.

---

Here's a list of posts created so far on the subject of Linear Approximations and Differentials:

1. Linear Approximations Part 1 - Interpolating between Empirical Data
2. Linear Approximations Part 2 - Estimating values of f(x) = √(x+2) near x = 2

---

Please give me an Upvote and Resteem if you have found this tutorial helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu