Probability (P1 Exam Practice) - Probability Distributions
Actuary Exam P1 Practice

Probability distributions are not hard to understand, but there is some Calculus used to do the problems given on the exam. It is not hard math, just basic Algebra, but there is a lot to memorize. If you want to research this further, look up Derivative and Integral videos on YouTube or Khan Academy. I may do a section for you after I take the test, so hold tight!
The Basics of Probability Distributions
A probability distribution the likelihood of an event for continuous or discrete events. Mathematics makes it easier for us to understand why it works because all of our curves have an area of 1 which is equal to 100% (probability-wise). The pf, probability function, and pdf, probability density function, are necessary to understand.
The pf tells us probabilities of events. The independent axis (horizontal) represents events and the dependent axis represents their probabilities. Here is an example of a discrete pf. Recall: discrete means we are using integers, -1, 0, 1, 2, ...
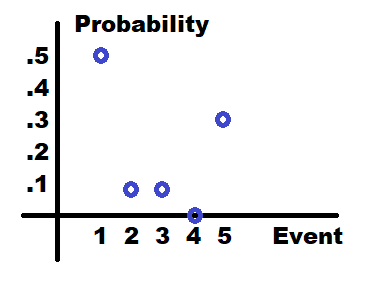
The pdf in Calculus represents the integral (anti-derivative), or area under the curve, which we know is equal to 1 for the entire set. This graph can tell us the probability of multiple events because you can find the area under the curve for certain bounds. Since the area of the pf is 1 and stops, that is the limit of the pdf
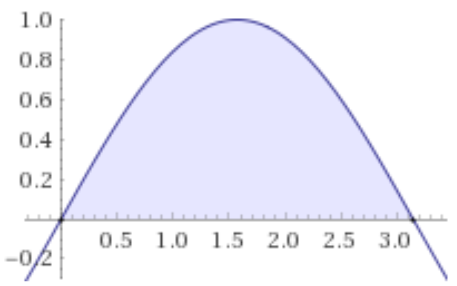
Graph created with WolframalphaIn a continuous graph the probability of a single event is zero. The whole graph still has a probability of 1. For example, light bulbs only last so long, right? Some last 3 years and some last 10 years. There is a probability distribution for this light bulb and it can tell us the probability it dies in a 3 month span, but not at a certain point in time. You could limit the function to a certain second, but what would be the use of that?
An Example with Calculus
The pdf for a certain random variable X is
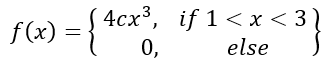
To solve for c we need to take the integral and set it equal to 1 because we are forcing it to be a pdf in a way.
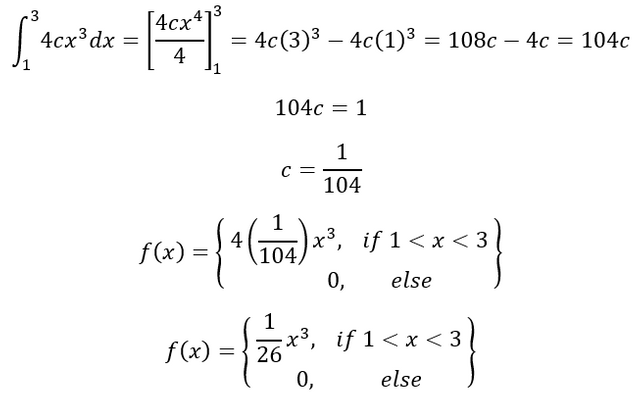
The graph for this:
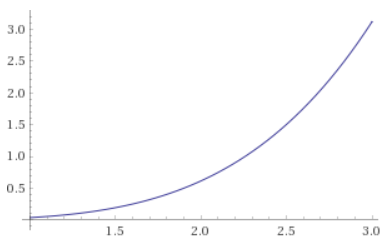
Example
The random variable X can take the values 5, 7, and 9 with probabilities .25, .14, and .36. For the interval (2,4) the probability density function is f(x) = 1/6x.
What is the probability that X lies within [3,6]?
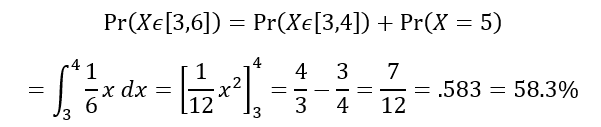
What is the probability that X is below 3.5?
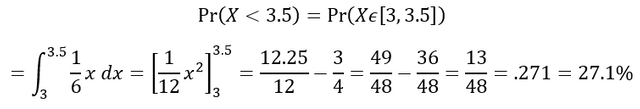
Distribution Functions
The distribution function for a random variable X measures cumulative probability. This means that the end of the graph will level off at 1 and flatline after that. It has limits defined with mathematics:

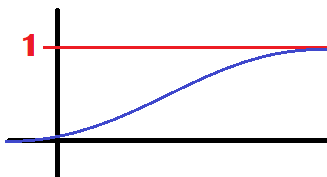
For discrete functions making this graph is easy because you just add up each probability cumulatively. For continuous functions, we can create this graph using this formula:
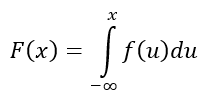
The Quantile Function
The quantile function is the inverse of the distribution function.
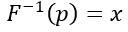
It produces x-values at which probabilities occur. We can relate it to quartiles (25%, 50%, 75%) used in basic statistics and box and whisker charts.
The Bernoulli Distribution
The simplest probability distribution. It is discrete and can only take the values of 0 or 1. It is great for modeling trials that either fail or succeed. p represents success and q represents failure. It follows that 1 = p+q.
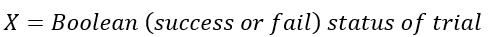
The Equation
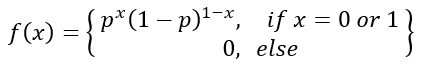



@hansenatortravel, I gave you a vote!
If you follow me, I will also follow you in return!
@hansenatortravel that's a really complicated calculus probability question for me lol...it's great that you are awesome at this! I recalled my pre-calculus and calculus classes but since then hadn't pursued with the math or science fields so had forgotten it. It's a good refresher and easy to understand~ Anyhow, haven't been on Steemit for some time as my Macbook black screened on me~ Hoping to get back onto Steemit and stay connected and support each other. Upvoted to support~
Sounds great @miss.kat. Glad to see that you are back! I think most of us have experienced our fair share of problems with technology. Thank you so much for the support! Can't wait to keep up with you as well!
Haha yes I’m back once again following the major hardfork 20 update n days of inhibiting me from posting or responding!!! Technology....my goodness this one had been quite an impactful one to all steemians!!!
Posted using Partiko iOS