The purpose of these posts are mostly selfish, but aren't they all? Haha. I am just doing my best to summarize what I am learning, or what I feel is important enough to note, for myself and those that want to do more with their lives, but don't want to read a whole damn book. I am first and foremost a mathematician, so I don't like to read. Hope all is well! Enjoy!

Chapter 5 - Theoretical Pricing Models

A trader that expects the market to rise will be more inclined to buy calls and sell puts.
Suppose that a 110 call expiring in three months is available at a price of $2. If the stock rises to 115 by expiration the trader will profit $3 ($5 intrinsic value minus the $2 cost).

The Importance of Probability

Expected Value (Mean)

The text gives two examples:

A fair die has an expected value of 3.5 because the mean is calculated by:

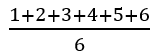
It is simply an average. Say you charged someone 3.60 for a die roll and paid them whatever they rolled. You will have an edge!

The same applies to a roulette wheel. There are 38 numbers, 0-36 and 00. The casino pays back $36 for a win on a single number. Therefore they have an edge that we can calculate:



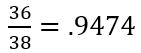
This means that for every dollar spent on the wheel they can expect an average payout of .05. Over millions of attempts they will win because of the edge.

Theoretical Value

The theoretical value of a proposition is the price one would be willing to pay now to just break even in the long run.

It is important to remember that just holding money gives it value in interest. If we take the same situation above, but the casino charges .95 instead of 1 and hold the winnings for two months they are still making money because of this fact. If interest rates are 12% annually we have to do some math:

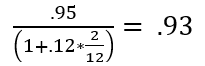
The player loses .02.

Because an option’s theoretical value is based on the laws of probability, which are only available in the long run, the trader must also consider the question of risk.

A Simple Approach

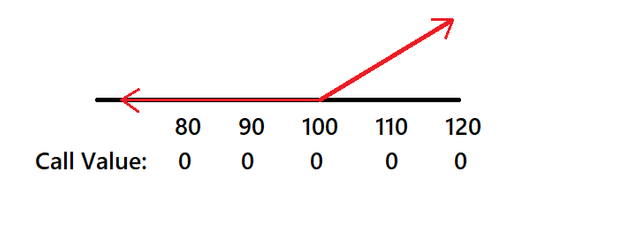
Natenburg is trying to make this easier for the reader to understand my making an extremely simplified model. For instance, consider that a contract can expire only at 80, 90, 100, 110, 120 which are all equally likely, so 20%. We can calculate the expected value at expiration to be:

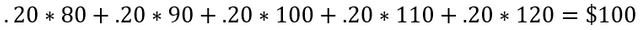
Now consider the expected value of a 100 call using the same underlying prices with a parity graph. We have the math:



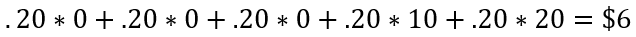
The expected value for a call at expiration is:



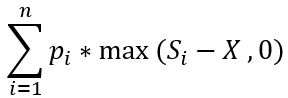
This is just a difficult way of saying the sum (add up) of all probabilities times the max of the underlying price minus 100 versus 0. Therefore if S-X is negative, you make no money, but it still takes up that probability. A put is the same formula, but it is X-S because you want the price to decline:



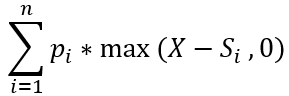
We can observe the parity graph for this situation:



So, you as the trader, if paying $6 would be losing interest on that money, so account for it here:



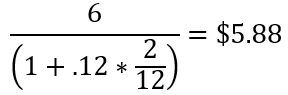
This number represents the value of the option.

The book then shows a similar example with changing probabilities, more like the real world, but still very simplified. Prices in the market can be anything, 95.243 or 110.12, but these examples are great to make sense of it. We want to provide these probabilities in such a way that the expected value that the underlying contract represents the most likely, or average, value at expiration.

Investopedia Definition: Arbitrage-free valuation is used in a couple of different ways. First, it can be the theoretical future price of a security or commodity based on the relationship between spot prices, interest rates, carrying costs, convenience yields, exchange rates, transportation costs, etc.

Remember that arbitrage is a risk-free trade. If we assume that the underlying market is arbitrage-free, the expected value of the underlying contract must be equal to the forward price.

Necessary steps in developing a model:

• Propose a series of possible prices at expiration for the underlying contract.
• Assign a probability to each possible price with the restriction that the underlying market is arbitrage-free – the expected value for the underlying contract must be equal to the forward price.
• From the prices and probabilities in steps 1 and 2, and from the chosen exercise price, calculate the expected value of the option.
• Lastly, depending on the option’s settlement procedure, calculate the present value of the expected value.
  

The Black-Scholes Model

To calculate an option’s theoretical value using the Black-Scholes model, we need to know, at a minimum, five characteristics of the option and its underlying contract:

• The option’s exercise price
• The time remaining to expiration
• The current price of the underlying contract
• The applicable interest rate over the life of the option
• The volatility of the underlying contract

Black and Scholes also integrated a risk-less hedge. For every option position, there is a theoretically equivalent position in the underlying contract such that, for small price changes in the underlying contract, the option position will gain or lose value at the same rate as the underlying position. To take advantage of a theoretically mispriced option, it is necessary to establish this risk-less hedge by offsetting the option position with a theoretically equivalent underlying position. Whatever position we take, we must take an opposing position in the underlying contract. The correct proportion of underlying contracts needed to establish this risk-less hedge is determined by the option’s hedge ratio.

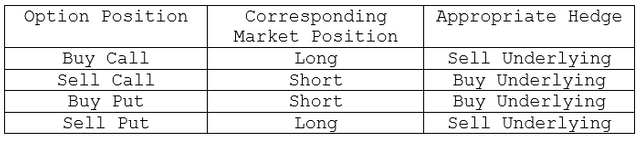
Exercise Price

The underlying price is fixed, so it is a constant that you just plug into the Black-Scholes equation.

Time to Expiration

This is also a fixed date based on the contract, but as time goes by the expiration closes in and the deal will have to be made (or not). If the holder of the option chooses not to accept, then they have a loss on their hands! Number of days until expiration is what must be considered by the model. It is necessary for two things:

• To determine the likelihood of a price movement in the underlying contract.
• To make interest calculations.

Remember it is only business days that need consideration since the price does not change otherwise. A trader may use hours or even seconds to get a better prediction, but it is limited computationally.

Underlying Price

At any time, there is a bid-ask spread¬, so the price is not always defined. Yes, stock prices are set when you are using an exchange, but the first buyer and first seller on the list may not see eye to eye leaving a gap of usually pennies. Usually, the underlying market is very liquid meaning it has narrow spreads, so the trader can take an average and use it for the model.

Interest Rates

Affect the forward price of the underlying contract. Interest rates may affect the present value of an option. As interest rates are raised we reduce the present value of the option. For foreign currencies there are two interest rates that must be plugged in, a problem that has been dealt with by Garman-Kohlhagen version of the Black-Scholes model. Traders often use the LIBOR, the London Interbank Offered Rate, or the Eurocurrency market to determine the rate. Interest rates tend to play the least important role in the model.

Dividends

A dividend is a payment to the holder of a stock. The amount of the dividend and when it is to be paid is the necessary information needed. An option trader is likely to focus on the ex-dividend date, the date on which the stock is trading without the rights to the dividend. The exact dividend payment date is important in calculating the interest that can be earned on the dividend payment and thereby calculating a more accurate forward price.

Volatility

The most important number to plug into the model to make good trading decisions. Volatility, we will talk about later, is the degree at which a stock price can change, statistically speaking.

Thank you for visiting my page! Feed Your Brain & Best Wishes!