The Number One Fix to Improve Steem's Chances for Mainstream Adoption
Meow. Here's a story.
@trafalgar is one of Steem's larger investors that actually bought into Steem with their own money. Maybe about 600,000 Steem Power in bulk when they started off a user like the rest of us, testing Steem as a social content platform. You can't get more skin-in-the-game than that.
They have been complaining about Steem's voting problem ever since figuring out Steem's sad state of affairs, which is where we are nearly at now when more and more users start clawing back most of their votes which is not quite social. The symptoms of it are all around us. Regardless, they've even created pure self-voting accounts to join the race to keep up and ironically, adding more to the problem.
"As I've argued before, this is not a problem of individual misbehavior or bad culture or inability to discover good content or bad ui etc. We've just got a flawed economic system that provides the very action we don't want with the highest rewards."
"And realizing the fact that if all the stakeholders behaved contrary to their direct economic interest it'll be better for everyone including themselves is not a solution. No individual stakeholder can entirely trust the voluntary generosity of other stakeholders. And the only way to defend your own stake is to contribute to the very behavior that's making it worse for everyone."
It's clear they don't like doing it, and would rather much prefer the economic incentives change so that they could start voting more on other better contributors besides themselves. It's just common sense. In all likelihood, there are certainly many users out there that contribute to the platform more than ourselves.
Why focus on being a social content platform?
Given that Steemit is unlike Reddit with its novel use of currency, we can expect that it’s also unlikely to function close to the social content platform that we know and love. It's somewhat a different beast. But we’d want to follow a proven path and evolve from there. It’s a sound strategy.
But what use will a Reddit-like platform have anyway if it distributes currency? Well, it maintains an engaged community, a community that gets paid for their contributions. So unlike Reddit, Steemit could sustain and grow autonomously with its own community and economy, thereby becoming a blockchain of opportunity of sorts.
But for this to happen, the money aspect really has to be managed to at least maintain some form of Redditness - a social content platform that works.
So with Steemit, are influential voters voting others more freely than themselves, given there's money involved? At the time of writing, it has been proven that it's an activity that's reducing over time under Steem's current economy.
This is why we need to understand the counter-productive activities that arise when money is involved in such a platform so that we can begin tame its side effects via economic designs to actually enable a social content platform. To do that, we would need to minimise the trolley problem in design as presented in my previous post.
There is no problem with profit-maximisation.
The problem is really just the abysmal alignment of incentives that is turning Steem into an economy that rewards the most counter-productive elements of the platform more than it should. Nudge profit-maximisation into a direction that benefits the platform instead.
It has all been reasoned out very well, in my opinion. Here's what @trafalgar mentioned recently:-
"I still believe with the right economic adjustments, we can make desirable behavior provide competitive or even superior returns to the problematic profit maximization behavior we have currently. Something like 50% curation, modest superlinear (which would incidentally solve most of the spam problems we currently have as well) and increased downvote incentives would be a good rough guide."
As simple as that. For the meatier version of @trafalgar's reasoning, check out this link: https://steemit.com/steem/@kevinwong/time-to-wake-up-and-fix-steem-s-voting-problem#@trafalgar/re-kevinwong-time-to-wake-up-and-fix-steem-s-voting-problem-20180525t145649133z.
It also pays to note that he's not the only one. Many have complained along the same lines for a much longer time, like @ats-david.
Never been so flabbergasted.
So I'm quite surprised when I found out almost no developers and top witnesses were taking @trafalgar's suggestion seriously as they seem to have rambled on about it for the past year. You're getting actual feedback from the wiseguy who's exploiting the bejeezus out of your system in broad daylight (albeit in good taste when compared to others, in my opinion), have decent suggestions to improve things, and nobody's feeling the urgency in doing something about what he's saying?
They and many others have been giving feedback that Steem's economy is currently paying out $1000 everytime people take a dump on the streets, yet somehow the focus is on building skyscrapers to attract tourists to shitcity 2020?
Don't get us wrong, we love SMTs and all those wonderful ideas that are coming in and inspiring people the world over. Even I'm working to get app developers into the idea of SMTs. But @trafalgar's suggestion is something that seems to require the least effort with a very high chance of immediate improvements. It's so bleeding obvious and non-trivial once you think about it. Why not try?
Steem is a lot of things.
But first and foremost, it functions best and may have the best chances for mainstream adoption through its social content platform. Steemit has been slipping off the web ranking over the past year because it's just not working out at the moment. Anti-social activities are now getting the highest rewards.. on this platform that could very well be popular if it's actually works like a social content platform.
We've tried n2, we've tried linear. Now it's time to try something in-between, along with some minor tweaks derived from the input of dedicated and experienced users. Minimise the trolley problem. Tame the counter-productive side-effects of money in order to produce the world's best incentivised blockchain-based public content platform.
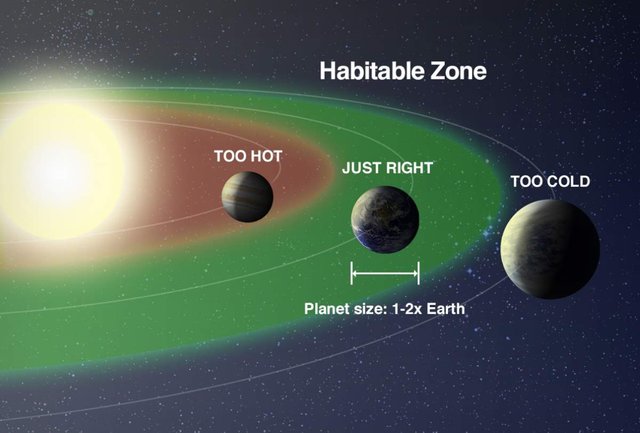
Planet Steem may have been orbiting too close or too far away from the Sun all these while. Let's continue to look for the region where it'll flourish.
Image source: https://ourplnt.com/nasa-announces-10-new-earth-sized-planets-orbiting-in-habitable-zone/habitable-zone/
cc: @ned, @andrarchy, @gtg, @jesta, @roelandp, @timcliff, @good-karma, @ausbitbank, @thecryptodrive, @someguy123, @aggroed, @clayop, @lukestokes, @smooth, @netuoso, @blocktrades, @anyx, @jerrybanfield, @curie, @pharesim, @followbtcnews, @xeldal, @pfunk, etc.
We're convinced that this is the best move for Steem at the moment. It'll be a huge mistake to just leave this unattended until SMTs and communities. The problem will still linger around.
Let's do something about it.
Resteem and upvote this burger!
(Or post up your own opinion burger)
(I'm seriously getting sick of rambling)

So cute
I feel like these discussions, while good and healthy, will quickly become largely irrelevant and overall frame Steem in an unsustainable way, leading us to address the wrong problems!
No matter how we incentivize these ROI maximizing whales to curate better or worse, the average user will not notice one bit of difference when Steem is at any sort of reasonable scale.
Let's say in the next few years Steem hits 25 million users. Great, but that still is only a tiny fraction of the bigger players. The Steem blockchain is currently dishing out roughly 25 million Steem a year in rewards. Even if everyone earns identically in a wonderfully balanced and sharing society... we all earn 1 Steem a year. Of course, this won't happen. Serious content creators, businesses, celebrities, etc. will of course outperform and we'll fall into much more of a Pareto distribution. Your average run of the mill Steemian will probably earn .1 to .2 Steem a year. If some misbehaving whales knock that down to .09 or .18 how much will it really matter? Will appreciating Steem price help save the minnow morale? No. Lets say the 25x growth in our user base brings on a 100x multiple in our price and we're at $300 per Steem! Your average user is still making $30-$60 per year. We cannot make rewards for average users our main message and reason for being or Steem will fail.
I grind my teeth as I see the countless posts being bandied about at this early stage, complaining about the seemingly small rewards , as I feel like the amounts anyone is seeing now will seem like a fortune in the months and years to come!
Steem needs to be framed as the incredible tool that it is. A one stop setup for businesses and creators for extremely frictionless and cost effective financial transactions, marketing, social media, crowdfunding, etc. In the end we're going to need people to be here just because they want to be here... not for rewards distribution. And those people will follow the content that they want to see.
I'm also curious to see the evolution and impact of a system like SMTs. New niche specific whales will be created and average users will have much more opportunity of feeling engaged and valued as they earn recognition and rewards in a focused community and area of interest that they really care about.
The ROI maximizing habits we see at this small scale will also cease to be as effective with growth. It really is short sighted both for Steem as a whole, but also directly for the people engaging in it right now. Sure, users may feel like they are maximizing their stake, but the ways they are doing it will lead to them not being able to outperform their own stake. I firmly believe that someone who wields stake wisely to build an active, supportive, organic community around themselves will outperform the ROI of a dedicated self voter or bot delegator any day, and this will become much more apparent the more people we have involved. Accounts focused solely on immediate ROI also tend to comparatively weaken over time, as they are more inclined to power down and cash out some earnings. Their quest for raw ROI already shows they have the mentality of a Steem earner, and not a Steem owner.
In a nutshell, I don't see the current economics as overly limiting or negative. There is no solution for the drastically increasing scarcity of Steem and at full scale the vast majority of Steem users will have relatively low value accounts regardless of the voting behavior of a handful of todays current whales.
Thanks, but I'm puzzled by your response. There's a problem that needs to be fixed now, which is the misalignment of incentives. Whether relevant or not next 5 years, it doesn't matter. Some superintelligent AI might even take over the world tomorrow.
Minnows or whales or giraffes, doesn't matter. What matters is to have an economy that is rewarding desirable behaviour, probably equally as much as the worst, if we're to be pessimistic. Now the gap is in the region of 600-1000% (I'm a normal user that curates, but I'm earning 600-1000% less than if I just sell my votes?)
I actually agree with most of what you have to say, but that's far in the future with the maturity of SMTs and all the skyscrapers that go with it. The goal of having a reliable focus now on the proven model of social media is the most beneficial move. Steemit and other Steem-based platforms could be leveraged, and I think most are underestimating web rankings and what they do for projects like this.
Also, 1 million engaged and satisfied users / investors / whatnot is way better than 25 million users under the current economic circumstances which rewards the most counter-productive behaviours for the network..
I don't think this focus will address the wrong problems. Sure not everybody is gonna get Steemed up, it's just the nature of any social networks. It really doesn't matter if there are a lot of people just earning 60-100 or whatever, the point is to have people actually earning through proof-of-brain, which at least require a form of curation (which is simply not voting for the self because it's the equivalent of no work. but we don't ban self-voting, we just remove the trolley problem so voting however one wants is more or less the same outcome).
Seriously I dunno why you're trying to brush off the issue when there's good evidence and reasoning lol. I think it's an entirely fixable issue at almost no risk, except to bidbotters maybe. So they'll need to shift to something that actually does some work instead of zero work.Regardless, they'll still exist, it's just that buyers would have to take more risk.
Agreed. People will come for the community and discover new things and do new stuff and figure out what Steem is for themselves anyway. But the chances fall off when there's utter looting going around. Also just saw the comment about celebs endorsing. Totally, it'll be the smartest move, especially once this problem gets fixed.
I do understand your point of view, but perhaps I'm just not optimistic on the ability to figure an ultimate ROI formula that incentivizes good behavior. I feel like cultural change and UI improvement is more important going forward.
Maybe I'm just missing how some of these suggested changes even work to properly address the issue at hand. In my mind, most folks who earn via vote selling are doing so by delegating power to a service that then pays them a percentage of their earning in turn. These voting bots are then dominating curation rewards as well, and under an increase in curation % will adjust by passing on more of that profit back to their delegators, thus keeping vote selling in equilibrium with actual curation.
And it doesn't seemingly do anything to address multi account abuses. Any kind of collusive voting ring will see no impact to their activity as it'll just shift which account involved gets the ill gotten gains. Likewise pure self voters remain unaffected as it'll still be more profitable for them to vote themselves as gaining the curation reward and the creation reward is better than just curating.
Maybe my thinking is off on some of these points, so please feel free to correct or hit me with some examples, but overall, I believe that whatever math we do, there'll be follow up math to determine the best way to game the system. Even with changes to make rewards non linear again it'll still be a solvable problem for ROI maximalists resulting in regular users still not getting curated. Voting trails would simply return in force to pile on predetermined posts at the most mathematically beneficial time to maximize rewards. For a small segment of the population, proof of brain will always end at the point the numbers are crunched and the bot is programmed.
All that being said, I don't think it's hopeless to expect changes and better things for Steem. But that kind of gets me back to my thought that some of these discussions may take us off course. For example, I firmly believe the best way to undercut the voting bots is to replace and improve the existing inbuilt promoted & advertising system. A well implemented and working system would give people a choice, and go a long way toward undercutting the profitability of vote selling services and improving content discovery, as well as bringing users a secondary revenue stream that would actually be valued based on their genuine audience size & engagement, rather than the amount of Steem Power they currently hold.
Perhaps I favor a more bottom up approach, rather than top down. I'm kind of working off the assumption that the "power users" are going to find ultimate ROI at the expense of the spirit of proof of brain no matter what. On the flip side, the vast majority of average users don't even fully grasp the mechanics of the rewards system as is, but they're the mass consumer feeding the vote buying industry because they see no alternative. They're the ones whose behavior can most be changed to improve the platform. Peer to peer advertising programs, public education about the importance of powering up and exercising your votes, and perhaps on the technical side continuing to look at the problem of the "dust threshold" taking away voting power of the smaller users. I just find things like this as being more important and productive than trying to calculate a new rewards formula that will maybe improve the voting patterns of a couple dozen individuals.
that's like saying we would literally push our nose up Zuckerburg's face same way Spiegel did with Snapchat. if that is so then a hell lot of work will be inputed into this platform. off the top of my head, i think the fastest way to achieve this is by luring CELEBRITIES of all walks of life away but most especially those from the entertainment industry.
is there really any other way of triggering up such mass adoption?
does history have any record of mass adoption that didnt end up through the Entertainment industry?
I see that as the most probable path too. I get excited whenever I see someone I recognize has joined the platform. There’s a growing core of actors, musicians, writers, directors & artists that I hope are poised to build more serious momentum.
But I think once communities and a bit more polish to usability (and of course registration) are added, there is an unbeatable value proposition. Right now people come to Steem and alter their behavior to chase rewards. I think soon the available tools and projects built on Steem will make it easier for people to cross over and continue doing exactly what they’re doing. And if SMTs perform well and development grows easier, the end result is people won’t even have to cross over because Steem will come to them. As an artist, I fantasize about a scenario where a site like DeviantArt integrates a Steem backend. Totally doable as a project like BeScouted has already demonstrated. I would jump for joy as 26 million new artists were suddenly on the blockchain. Scenarios like that can feasibly penetrate across every category of online community that exists now.
Meanwhile, down in the three- and four-digit accounts, we're finally developing multiple independent systems where dolphins and minnows are helping each other and driving collective growth. We're developing high-value, externally-appealing content, onboarding a bunch of incredibly-talented new users in non-cryptocurrency topics, and making sure they're financially and socially rewarded enough to stay. The concept of cooperation among an expanding middle class is gaining traction.
Basically everything linear rewards promised is starting to happen. Our share of the rewards pool is small but it's growing and if things stay as they are it will continue to grow. I'm not convinced that's true under your plan.
There's a double economy on Steemit and I appreciate that yours is both much larger and pretty much a mess. But we're making actual progress down here and if you give us time we'll reshape the face of things.
I understand there's this value adding layer that's going on all over. But are they going to provide 600-1000% returns more than if I just self-vote and vote trade all the time? If this layer can inch things closer to just a mere 50-100%, then maybe a revolution will begin.
Basically, come up with something that even the likes of @freedom @trafalgar and @haejin will act for the greater good. To make this happen, voting has to be almost synonymous with acting for direct self-interest as well. Learning from them, I think we can come up with a better kind of money that really flows around. I don't think any "layers" will change the core condition. But for sure I think they'll be massively useful when circumstances are right. Hence this proposal.
Thank you very much for contributing to the platform, although please note that you're funnelling in and maintaining users in a place where the incentives are totally out of whack. You can literally see the most braindead behaviour getting the highest rewards. Steem's economy is now paying people $1000 everytime they take a dump.. and there's really nothing to stop it.
Hopefully the proposal gets taken seriously so that builders like you wouldn't be working against highly unfavourable circumstances in the future. Which projects are you working on by the way?
You seem to think I'm here looking for your support. I'm not. I'm here asking you to leave us alone. Go ahead and have your huge ROI. That's fine. Just don't prevent hundreds of people from helping each other in hopes of forcing a few users you dislike to begrudgingly do something they don't have any interest in.
If you would like to support the building community, I'll offer you something you can do for free: make some curation posts. Find 3-5 posts you like and write about why. Or pick a user you think is doing good work and write about why. Self-vote and vote-trade your post into trending and take your profit. You have a huge audience and you could make a difference without ever passing down a cent.
50% curation and superlinearity of rewards are even-more-highly-unfavorable circumstances for us than the existing ones even if they actually do what you think they will. They raise the minimum effective buyin, which is already way too high. They result in everyone relying on the regular support of ~150 whales who you've forced to show up rather than being able to build a larger community of people who are actively, personally interested in helping each other succeed. Which is the real long-term value here. Under the current circumstance we have enough voting value to drive the growth of that community and inspire more users to participate. Under superlinear everyone trying to do that would need a consistent whale. And there aren't enough whales to do that sustainably, even if you could control them all.
Find a system that allows builders to help other builders and it will be worth thinking about. Hyperbolic rewards would be better than superlinear ones: make it easier to go from 500->5000 and 5000->50,000 than it is to go from 500,000->600,000, instead of the other way around. Find a way to allow more people who aren't crypto millionaires to buy into the system and be effective. That's the support we need. We don't need whale votes, we need to not need whale votes.
I see some promise in the algorithm @t3ran13 uses if you'd like a place to start. (That's not a project I'm involved in, I just thought it was cool. I literally have no idea who that user is.)
thx)
Nope, I wasn't thinking you're here looking for support. I was just replying plainly. Personally, I think your all suggestions would work against the platform, especially hyperbolic curve. But that's only my take on it. I've been supporting various communities the past 2 years and have been losing out on that big ROI, hence my complaint about it recently. Many more will just start selling their votes and do nothing. Thanks for the recommendation about @tran13's algo, by the way, will check it out :)
To be clear, I'm not advocating for a hyperbolic curve. I think it might be better for the platform itself but switching to it would definitely crash the price of Steem, and it probably couldn't be done effectively anyway. I just think superlinear is even worse.
I hope you don't think my suggestion of you making curation posts is bad for the platform. If you listen to any of this I hope it's that paragraph.
It's a good suggestion and I'll consider it, although in general I wouldn't wanna pump out posts like a tv series and would prefer to write my own stuff when I have the time and support through votes. I get that it helps parts of the community though. The problem with the current economy is that it wouldn't help as much as before. I remember a time before linear when good contributions were likely to get more attention, and now it's just too spread out. I think you may be underestimating the side-effects pure linear has. Sure it provides full individual autonomy across the board, but it's at the expense of something else, hence my suggestion for a slight superlinear to have any semblance of collective work.
I'm glad to see more and more posts about this topic, @kevinwong. Sometimes it feels like no one is listening, simply because no one appears to be talking! It's so important that users from brand new minnows all the way up to long term investors provide their feedback and their experiences to be considered in however we move forward. Seeing big accounts start talking about the culture and the necessary behavioral shifts is awesome, because we're starting to see followers who had previously not weighed in joining the conversation. Posts like this one are valuable, because it's opening up debate and discussion to audiences who may not have participated before, and that's a good thing for a solution that is well rounded for everyone involved in this blockchain.
There has absolutely been a solution suggested that has included modest super linear rewards, 50% curation, and a separate downvote pool. There have also been counterpoints with ideas like an adjustable curation rewards rate that begins at a 50% default, but can be adjusted by the author. I think, overall, that almost everyone is waking up to the fact that some changes are necessary. We have to keep these conversations lively and representative, because content producers, curators, developers, and investors all have valid viewpoints that are interconnected in how we approach addressing the issues we have now.
This is part technological, and part societal. Any code changes made need to drive the behavior we want to see on the platform, and the behavior that we value on the platform needs to be examined to inform our decisions on the technological development.
Appreciate the response @followbtcnews. I think I'm learning about the process a lot since I've never put up any serious complaint before until I started to be convinced that this is a fixable problem, and a problem that has been plaguing the platform.
Glad to hear that, I may been ignorant about what goes on between witness and dev talks. Now my biggest worry is, are there any "protocols" between devs and witnesses in trying to converge on a solution? It seems to be a problem that has been left hanging for too long..
Lots of great thoughts here, Kevin. Many of them have been discussed at length, and I do think we’re moving towards more consensus through these continued discussions. I don’t know if we’re there yet.
While you and I might say, “Yes, we need a separate downvote rewards pool to encourage effective protection of the rewards pool,” some people are arguing to remove flags and downvotes all together because they’ve been so abused by retaliatory flagging by large SP accounts. If flags can’t be countered in the last 12 hours before payout, and we start rewarding flagging directly (instead of the current indirect reward of protecting your overall, long-term investment), will we create new problems with more people leaving and complaining about being “censored” because “their” rewards were “taken” from them? Many people don’t understand potential payouts or what true censorship is. We have education work to do there.
I think some changes to the reward curve to give a little extra rewards for pile on voting could be healthy and Dan talked about his concerns over linear rewards early on. That said, I also remember when so many people got absolutely nothing for their content and how linear rewards enabled them to get something, even without a trending post. Maybe a small change could be made here for a set period of time and then reevaluate.
I’m very interested in the 50% curation, but I’m also concerned it’s just funneling more rewards to those who already have a lot of Steem Power. Unless we adjust how curation rewards work, those with little Steem Power would earn very little rewards via curation so how will they ever get ahead, even if their content is great and begins to get voted on? I think some will complain the rich will just get richer if too much of the rewards focus on curation which goes mostly to those who already have Steem Power. Maybe it will incentivize more people to invest in Steem?
Part of me still thinks the problems here are psychological. If huge whales are trying to extract too much value instead of using the value they already have to protect and grow the collaborative commons we have here, then they essentially destroy their own provisions. If, instead, they thought in terms of rational, long term value creation (instead of irrational, short-term value extraction), we might all benefit more.
I know many disagree with me here and think it’s just about adjusting what systems are in place that people can exploit. Maybe they are right. I still think much of the value we see here is because of people who choose not to exploit, even if given the opportunity to do so.
Updated, added more counter-arguments:
I agree with most of what you're saying.I think this is a non-problem. All SP users would want to accumulate anyway, so why does it make a difference with a lot of SP? The rich will surely get richer regardless, if they don't waste their potential. The problem is getting voter's self-maximisation actions align with the behaviour that ought to be rewarded on the platform, which is curation / distribution / supporting curation services. The action has to be almost synonymous with SP accumulation, it's not a bad thing. I think with this, even the likes of @freedom, @haejin, @trafalgar will start to use their votes for the greater good.
They can work for curation groups like @curie which has already established a decent workflow that adds to the platform that can be replicated. Also, with a curation economy actually going on, more valuable contributions will likely get rewarded.
Re: about flags:-
Reddit has downvotes even for the end of retaliation, by the way. It's something users will need to adapt to. It's likely a feature that adds more to the platform rather than the other way around, imo.
This part I'll be disagreeing. Technology leads society leads technology, ad infinitum. The tech is making those being "rational" lose out too much, it's hard to tell people to change and there are no signs of users following what is considered the better course of action for the long-term. So the tech needs to enable profit-maximisation behaviour in better directions, which I think could be fixed as per the proposal. I think traf's explanations are very good here and it actually changed my mind. Like if Steem's econs is actually the equivalent of flying too close or too far away from the sun, then we're just fighting against all odds to make things work. Traf may not be making such an irrational move after all, since it's a problem that will likely be woken up to and addressed eventually at some point for a good dump, if the platform is still in public interest..
This is right of course, but doesn't address the problem. They're absolutely right.. what you've just said is almost equivalent as saying "it's okay, leak Steem's treasury to the worst behaviours on the platform.. it's okay, we moral upstanding people will take the hit until they go away.. somehow.."
Again, those taking a stand is currently getting "taxed" by the worst behaviours on the platform. On equal grounds, if SP accumulation points per month for those taking a stand and actually contributing to the network is only +100 points / month, while those exploiting are getting +1000 points / month. In 10 months, the difference is 9000 points. This is the chasm we're facing at the moment.. and good news is that it can likely be fixed, as proposed.
I also like the "flying too close to the sun" analogy. You make a lot of great points here, and I agree with them all. I do think value creation should be the focus AND those with a disproportionate amount of STEEM should individually restrain themselves from extracting too much value. This is the part that causes problems from a mentality standpoint. If the largest whales were to take the lion-share of curation rewards under a new economic system, we'd have the same problem again, just a different flavor. I agree, things can be improved, but there will always be "the problem" of wealth extraction until we think in terms of a collaborative commons and not in terms of a staking coin for maximizing wealth extraction.
Some more thoughts on this (which I think you've already seen): An Argument for Long-Term Rational Self-Interest Versus Short-Term Irrational Value Extraction. When people say no one is taking steps to add value instead of extracting value, I point to my wallet and say, "Really? No one?" I think many are, they just do it quietly. I'm happy with the amount of value provided to me via STEEM, and I don't need to use bidbots or self-voting to extract further value. That said, I also agree more can and should be done to protect the commons and disincentivize others from extracting too much from it.
Thanks for the response! Yup we're converging on something here @lukestokes :).
Now we're seeing value adding services popping up all over Steem. Their existence will likely have a much higher chance of greatly accelerating improvements on the network if those with a disproportionate amount of STEEM find a great reason to use them. The best bet is to encourage that action is the have a result that doesn't lose out in the order of 600-1000% compared to self-voting/vote-trading. 300% may still be too much of a difference to trigger a new behavioural equilibrium, a mere 50-100% difference in results may be possible for the revolution that we need. The problem is that value-adding endeavours are falling back by the order of 600-1000% difference.
I understand that we can promote the culture, but there are others that just want to maximise anyway. The wide gap is causing more and more to join the race, "succumb to the dark side". If the gap is not as wide, maybe it'll be more bearable for most users to do it for the greater good, so to speak. I suspect maybe you aren't "feeling it" because you're a top witness :D it's a different kind of skin-in-the-game..
Check out this video, it's very interesting, showing the difference between aspirations and actions..
This! 🙌
Good summary of the individualist responsibility / culture point of view. I think point of view contrasts with the view which places overarching systematic incentives at the core of positive behavior problems.
I lean to the latter. The incentives work whether or not you're aware of them or even factor them into your decisions because the create the outcomes and everyone responds to outcomes. This is where @tcpolymath gets it wrong too. Individual people "feel" the systematic incentives even if they are not aware of it. Rewards subtly (and not so subtly) affect what people determine is cogent to do.
I also think your analysis is wrong here:
It is not necessarily irrational to extract value in the short term, especially when you factor in the unknowable future, difficulty in coordinating among large stakeholders (ref prisoners dilemma), and so on. Changing the rewards structure is I think a good attempt to offset the unknowns and paranoia which is akin to FOMO.
You are both right and wrong imho. If the vast majority of people acted according to that principal it would work. However bringing that mindset about is about as likely as bringing about world peace, most people agree it is a good thing to aim for but it is never going to happen. Human nature just doesn't allow for it, no matter how much people think it should.
No system is perfect, there will always be bad actors but I have to agree with the OP, the key is to align financial incentives with desired behavior.
In trying to achieve that aim, I wouldn't get too caught up in "the rich get richer" mantra. It will happen or they will take their investment elsewhere and everyone will lose. So long as the poor can make enough to make their time worthwhile the platform will work and the cream will rise to the top or reasonably close to it at least.
Make no mistake, it will happen here or elsewhere but if it happens elsewhere this platform will go the way of myspace or bebo and become a footnote in the history of blockchain. It's just a question of when, not if.
I think this is a very good point: "If, instead, they thought in terms of rational, long term value creation (instead of irrational, short-term value extraction), we might all benefit more."
But the sentiment seems to be - someone else is abusing the reward pool so why shouldn't I do that as well ? You wouldn't want to loose out right ?
The whole idea of Steemit is to cut out the third party - greedy people like Mark zuckerberg - and we as a whole get to share the rewards of the value we create as a community. But that should also mean that we all take role as leaders. It is sad to see that it seems like we are in the end being just as greedy as any other and just like in Facebook just a few really benefit who are at the top.
On the other hand I don't have upvotes that would be worth 10 of dollars each so it's not easy to say what I would do if I had that kind of Steem Power.
Either way, I think 50 percent curation seems like a good option to try. But I think more importantly people have to think of their own social compasses instead of looking at what others do
Helo @lukestokes
Thanks for stopping by to offer your thoughts on this important subject matter.
I guess you vividly captured my mind here. If the system is skewed to put the rich guys perpetually at advantage, this could cause a lot of middle guys and new guys to leave.
Whatever the case, I guess steemit team and top witnesses will do what's best for us all.
@eurogee of @euronation community
The incentives are already good enough. All shareholders already understands that this is in their best interest to protect Steem blockchain from spam and abuse.
The problem is not with lack of incentives, but with to strong disincentives.
People are afraid of revenge when it comes to flagging. This is simple as that. Therefore we need a way, to allow them flag content responsibly without a fear of being flagged-back
That is not a primary goal of my upcomming project "Wise" (code name: SmartVotes), but it will also allow stronger accounts, to delegate flagging and delegate decision making to smaller accounts.
I think this may cause that owners of smaller accounts will become a little bit more brave.
More details about the project... soon :)
I've been really excited about this project since we first discussed it at a dinner table in Lisbon. :)
Hi @lukestokes ! Do you also believe that with SMTs and the type of airdrop that @steemhunt created will change the game entirely? Many individual accounts will stay with low SP due to the reason people will start delegating SP to Dapps that will be airdropping their SMTs. This will end up the Steem Blockchain with high power to Dapps that will give ROI to its users in different ways, like Steem and their own SMT.
I believe that will change Steem for good.
By the way, if you get the chance to review the post I made about registration for eosDAC and EOS, your feedback is well appreciated!
Regards, @gold84
Until SMTs launch, it's hard to say what will happen.
Thanks @lukestokes for your feedback!
Regards, @gold84
Bidbots are anti-social. Those are advertisers selling "visibility" while in reality; the operators and all those who delegate their SP to the bidbot are being paid to look away.
This was once called the "attention economy" and people are constantly talking about how the bidbots are becoming a problem; and nobody is paying attention to them.
These people cannot socialize with robots. They want actual eyes on their work, not 1000 eyes concentrated into one vote that isn't even worth the stated value beside their post. People have $50 worth of rewards next to their post and they don't even earn it. A massive portion of the reward pool dished out daily doesn't even go to these members who have it placed beside their work.
Hardly anyone is coming around to talk to them. The money seems fake and so do many of the members leaving comments. The actual feeling of being "rewarded" goes far beyond money and many of these people are being robbed of that experience. That experience existed at one time, before bidbots, and I know that because I was here enjoying it. I witnessed the negative anti-social impact of these bidbots since their inception and every step along the way.
That actual feeling of being rewarded and appreciated was one of the main contributing factors that kept me around for so long and I am damn lucky to still be one who gets to experience it to this day. That took hard work and dedication to maintain but many of these other members are not being afforded the same opportunities and ladder to climb. Many got duped into thinking this place was about easy money, they seem to think all they have to do is post and purchase their rewards to win, and they don't even give themselves a chance to learn about how hard work and dedication is a requirement if one wishes to succeed here. They get stuck between a rock and hard place and the anti-social elements caused mainly by these bidbots do not provide them with the incentive to stick around. They're performing in front of empty seats; and the audience that didn't even show up is earning more than the performer.
I politely disagree when you state bidbots are not a problem. They are a problem, but not the only problem. Maybe your cheeseburger will help. I hope everyone can put their heads together, combine everything we've learned here on Steemit so far through trial and error, and come to some sort of healthy solution that of course not everyone will agree with; but hopefully at least steer us all in the right direction.
You're right, it was part of the title I forgot to remove. Bidbots are a symptom of the dysfunctional economy. What I really meant was paying to get higher ranking like advertising. Now it's an issue because the cost is covered by the inflation, and even worse, with potential profit as well so it's at the expense of the network. Which all could likely be remedied as per proposal. Can't tell people to stop using or operating the bidbots, but the econs will find a new equilibrium that'll make curation groups more favourable, I think :)
I see now, you edited that portion out. They call it advertising. Mainstream media caught wind of our "advertising" and one of the first things they asked about was the obvious low quality paid programming style spam on our trending page. All that money that went to "advertising" shot us all in the foot.
The advertisers can have their money as well. Simply mark the posts using bots as advertisements, take them off the trending page and place them in the promoted tab. Then those who want to spend money on advertising can then pay ME, the content producer, to place a banner on my blog that leads to their promotion. Something logical like that works and there are far more winners. We see it on Youtube working great, daily.
I do see the potential there as well.
Great solution you've just proferred regarding bidbots, @nonameslefttouse.
I was a bit embarassed when the Bloomberg interviwer asked Ned Scott about how Steemit Inc. intends to solve the current problems of crappy content on the the trending page. Hopefully, most of the solutions would be considered by steem witnesses and core team members of Steemit Inc. for implementation soon.
@maryfavour.
Steemit was mentioned on the Joe Rogan Podcast as well and while watching on Youtube, I saw our trending page; along with over 1 million other viewers. We dodged a bullet that day. The content at the top was genuine and respectable. Two days before that podcast, the content was complete trash that involved members bickering and acting extremely unprofessional. Joe Rogan is a comedian and had he seen the trolling, there's no way he would have been able to resist making a few jokes.
This publicity is important. We need to get it right. We live in a time when cryptocurrency ads are being banned everywhere. One simple loophole to get around that censorship is to advertise Steemit, with no mention of cryptocurrency or any of the other wording they've deemed unfit for advertising such as "profit". That gives the STEEM blockchain another distinct advantage over all of the others; but not if people continue to fail at taking Steemit's potential seriously.
Steemit, Censorship Proof, Transparent Public Forum. I pitched this idea to the promo tag, nobody wanted to hear that, seems everyone in the Promo tag is high on @stephenkendal and mostly all about "MONEY!" and prematurely onboarding everyone under that empty promise of Making it BIg, instead of consciously stepping into the momentum of Facebook censoring as it's happening before the buffoons in Congress.
Money ain't gonna buy you friends, nor will money speak the truth on your behalf, and money ain't gonna reason how can you have any online or otherwise community without Moderation, fuck me even TPB has moderation AND curation.
I thoroughly enjoy your posts when I catch them and I couldn't agree more with your bid bot assessment @nonameslefttouse, I may be biased after all my proposal was to give even more power to the POOR bastards that hold nothing but REP but ain't anyone want to hear that, the only noise made was from @pharesim when he chimed in to tell me that REP doesn't mean shit. Well then I guess my entire proposal for a separate flagging system is shit, right @pharesim? JK, if I could give a fuck all about some nonsense like REP doesn't count as if code is some mythical creature that needs to be tamed.
I had seen it with my own eyes a couple months back when @dantheman told @the-ego-is-you that they were working on a separate flagging system apart from upvoting, and that was when I knew I had hit the nail on the head so hard that nobody could get a cat's claw under it and will remain there even if Stinc tries to scrape the entire thing because I realize one simple thing a long time ago: you cannot moderate with money as that is the equivalent of giving justice based on people's pockets.
https://steemit.com/blockchain/@dantheman/re-the-ego-is-you-re-dantheman-the-problem-with-byzantine-generals-20170130t142618756z
Insert whatever euphemism you want for shit coming back to bite you in the anus because @ned, ain't any SMT gonna solve moderation and ain't any moderation going to happen here without implementing something similar to what I suggested a year and some ago, which unbeknownst to me at the time that the man behind it all had divulged a telltale of being on top of the issue I shouldn't have even bothered to contemplate not even a month or so later, had he not ended up leaving this project. It doesn't take a genius to figure out that as long as anyone can spam and abuse the platform, wealthy or poor, the rest of the world will shake their heads at the car without brakes which is the perfect analogy for this contraption.
Don't worry, to put the reality of consequences into everyone I plan on revisiting my post from last year and including some caveats, such as Restoring/Recovering Steem through the flagging system, either that was lost (poloniex will get the boot at the curve) or hacked or misplaced, and outright freezing accounts and founds (poloniex will get the boot to the curb, along with hijackass and all other spammers and name sitting assholes @bah!!!!!!!!!!!!!!) and not only disabling accounts from spamming (@noganoo and his alter-dimensional trifecta of @gullible, @TIMOM and @notgayporn).
Wild West mothertruckers, if you plan on being a pathetic non-thought in your actions, with your stake, reap the consequences, because @dantheman when he said "Thanks. I can tell you that we are working to separate moderation (flagging) from curating (voting). This issue will be improved in time." to @the-ego-is-you's flagging appart from downvoting comment it was LOUD and CLEAR the age old issue of wealth dictating justice and not the blind justice we have.
Yeah, justice is a harsh word for this crowd to stomach, keep dreaming that anyone will enjoy this ride anymore once the masses dawn on the horizon with their no holds barred spam, plagiarism and outright abuse (can you scrub child porn from being automatically uploaded once dragged into the comment section and the comment not posted yet the link be used regardless? amazon doesn't care..)
I share the same opinion with you @nonameslefttouse on bidbots.
I joined last July and there were no bidbots and Steemit was awesome and i would feel good when people interact with my posts!
I could really feel rewarded for my content and btw its an awesome experience,however little the money besides the post was.
You could know a real human being read,upvoted and commented on your post,i felt encouraged.
The actual feeling if being rewarded is really now being missed by the new people as you say.
Its really rewarding to start from zero and grow on Steemit,make 10 posts and earn a combined zero,work harder and earn as you grow on the platform!
I have a challenge with the new people i bring to Steemit in Uganda(i am a Steemit promoter).
Whenever i tell them of the organic way of growth of commenting and starting small,most of them do not want to believe.
In fact am shocked when many ask me about Bid-Bots! I tell them to try as much as possible to grow organically as it is more rewarding than getting votes on a post which are all bidbots!
Anyway many people here are for the money(which is okay),but to me and may be others,we feel happpy when real people read and comment on our posts.
I also like the idea of 50/50 payment....it will make more people start reading and discovering more great content.
Hello moses i need to ask you something thia iz my WhatsApp number 0756125239 reach me pliz
This is quite informative. I just got enlightened reading this
I agree with the bulk of this except for one thing which I think it's truly broken and that is the curation system.
Back when we first started it did work as a way for good manual curators to try and find new and interesting content. Now though it is merely a pile on to posters who get good rewards.
Increasing it to 50 would exacerbate this I feel. People would still pile on to the posts they think will earn biggest rewards. Because they see the dollar signs of the big money.
And I know that the biggest curation rewards go to those posts that are discovered when they have little rewards already but it just doesn't seem to work out like people care about that now.
It's a tricky one. I think a slightly super linear approach to rewards would be good but that gives me the fear that the people who use multiple bid bots for their posts would abuse that as it were to then make a proper killing on their promoted posts.
Abuse will happen anyway, but point is good behaviours shouldn't be completely left in the dust. Moving away from linear also means posts would need to have votes congregated, so it's manageable. Under linear, the abuse is spread out and distributed widely.
Yeah, I'm with you. Something being done is better than nothing. Some right out of the box nonsense would be good :0)
I really loved your post. 😍😍
Thanks for sharing
Most welcome sir,
You are welcome
Please keep rambling Kevin! I honestly feel that you are leading the charge on this issue. You have my full support and resteems.
I agree completely, in fact I was reading one of Warren Buffett's shareholder letters and it had a point that related directly to Steem. He says, paraphrased: "We view it as less risky to find businesses with excellent management and fundamentals, and much more risky to find businesses that align with future trends and markets."
Right now Steem and SMTs are fully aligned with, as you say, "building skyscrapers to attract tourists to shitcity 2020", but we lack the excellent management and fundamentals.
I can't lie, I'm diversifying my energy a bit. I want to see Steem succeed but I view it as an increasingly risky investment of time / money / energy.
I think the team is improving and getting more streamlined after the new CTO came in. Decentralisation problems.. lol
There's so much good discussion in this thread I feel like I'm not qualified and my opinions dont matter. But fuck it, I feel that we need basic non-tech idiots like me joining the discussion too.
Let's just say that HF19 has morphed into a shitshow..
I dont see why these suggestions be implemented in the upcoming hardforks "just to see how it'll work out". We've already done it with HF19. Steem as a blockchain is plausibly still far too problematic for mass adoption.
While i think it'll never be fixed, we still should find a way to play around with the parameters and see what works in the real world situation (aka tested by the users instead of discussed hypothetically by smart people).
Overall i give an "aye" to your suggestions, if it means a damn thing.
I think it's worth trying something in-between. I suspect an overarching economy has a lot to do with psychology and human behaviour, and I think its effects are great underestimated. It sets the culture. With linear, it's basically a tragedy of the commons when every individual is allowed full freedom so to speak. It detracts from society. A social content platform needs some collectivity, hence the suggestion to move away from linear, even if a little. n^2 was too much of a sacrifice of individual autonomy.
"tragedy of the commons" is exactly what steem is right now. at this rate its gonna get run to the ground before too long and becomes a "zero trxn fee hedging asset" excuse of a coin by traders.
Cant say anything else other than i fully agree with your points.