Complete guide to understand rewards in HF21 [Part 2]
In the first part we saw the basic concepts and the convergent linear curve. This second part is focused in the distribution of curation rewards.
Curator rewards
The way rewards are distributed between curators is through "weights". Each time you upvote a post or comment you receive a weight, which depends on the value of the vote and the previous votes. At the end you, as curator, receive a percentage of the total curation payment which corresponds to the weight divided by the sum of all weights.
For instance, suppose your weight is 125, and the sum of all weights is 1000. Then, if the reward for curators is 20 SP, you will receive 20 x 125 / 1000 = 2.5 SP.
Do not confuse this curation weight with the weight of the vote, both are two different things.
And what is the formula to calculate the curation weight? When you upvote you are adding rshares to the post. The weight you receive is the difference between the new (rs1) and old (rs0) total reward shares evaluated in a curve W:
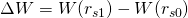
The curve W(x) is the curation reward curve. In the Hardfork 19 and 20, it was defined as the square root of rs, which leads us to a specific analysis. However, the changes in the Hardfork 21 introduce a new formula a little bit different:
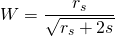
This change is not on a whim, it has its deep reason for being, and comes from a beautiful relation between claims and curation that must be preserved:
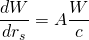
Where A=1/2. I will not go into details in this point, but just tell that thanks to this relation earlier curators have more benefits than late curators, and more important, there is no need to recalculate the weights of all curators when new votes come in.
Being rs0 the rshares before the vote, rs1 the rshares after the vote, and rsT the total rshares at the time of payout, and assuming no downvotes, the individual payment for a single curator is
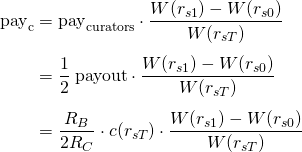
The reward system incentives to earlier voters. Thus the curator payout is very related to the gain that the post experiments after the vote. Let's define g as the gain in rshares:
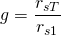
And "v" as the number of rshares is giving the vote:
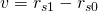
Then, the payment can be expressed as
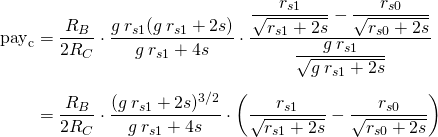
In following sections we will discuss different cases related to the value of 3 parameters: vote (v), gain (g), and previous votes (rs0).
Case 1: No previous votes. rs0=0
If the vote is the first one, rs0=0, and v=rs1. Then
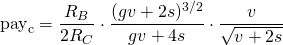
Assuming "gv" is much greater than 4s, and "v" much lower than 2s:
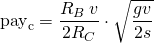
Assuming "gv" is much greater than 4s, and "v" much greater than 2s:
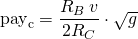
Assuming "gv" is much lower than 2s:
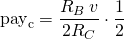
Case 2: rs0 much greater than 4s
In this case we suppose that the post is already popular and that rs0>v. Then
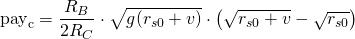
After some calculations we can get
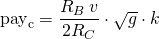
where
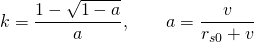
And k tends to 1/2 when rs0 tends to infinity. Then
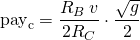
Case 3: v is much greater than 4s
In this case we suppose that the post is voted for a whale, and that v is much greater than rs0. Then, after some calculations we get:
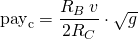
Case 4: v tends to zero
When the vote is very small we can use the derivative of W to calculate the payment to the curator.
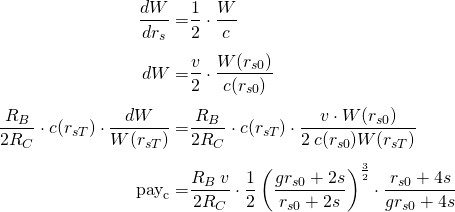
Assuming that "grs0" is much greater than 4s and "rs0" much lower than 2s:
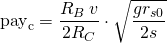
Assuming that "grs0" is much greater than 4s and "rs0" much greater than 4s:
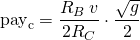
Assuming that "grs0" is much lower than 2s:
Patron
We can see that there is a patron in these results, and the payment to the curator can be simplified to:
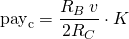
Where K is an expression that varies depending on the conditions of the parameters. Remember that v is an amount of rshares added to the post. Following the concept of linear payout described in previous sections, we can define "vote" as:
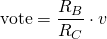
That is, "vote" is the value of the rshares converted to steem and supposing linear payouts. In this sense, the payment to the curator is:
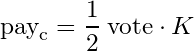
And the value of K is
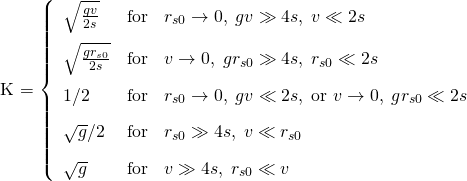
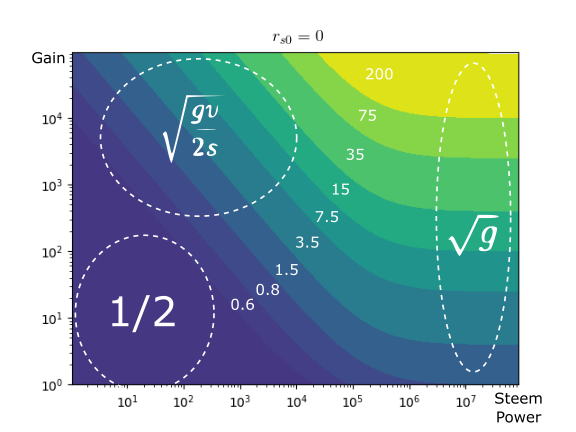
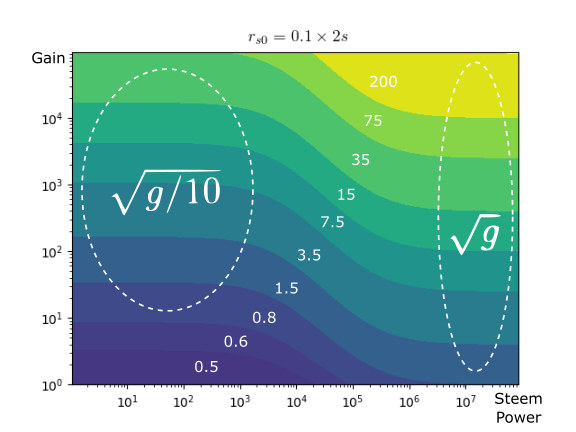
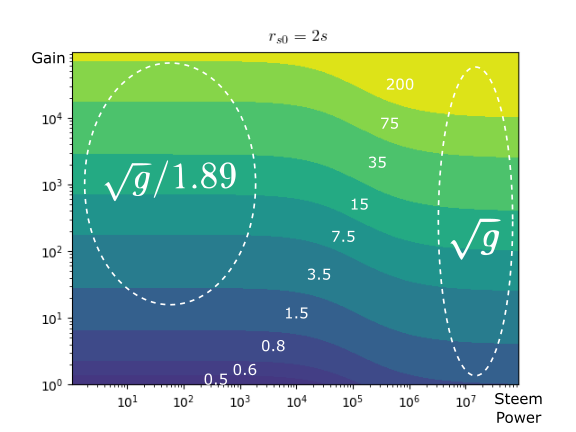
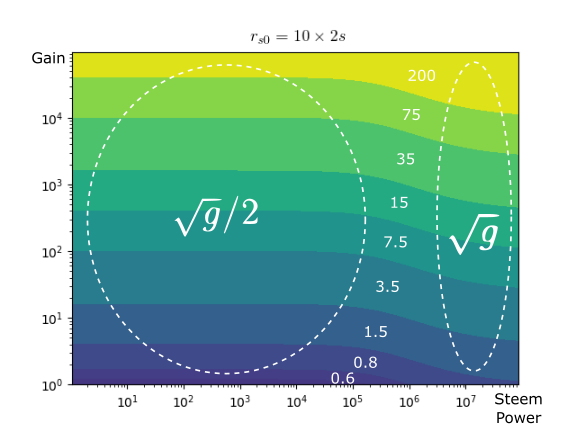
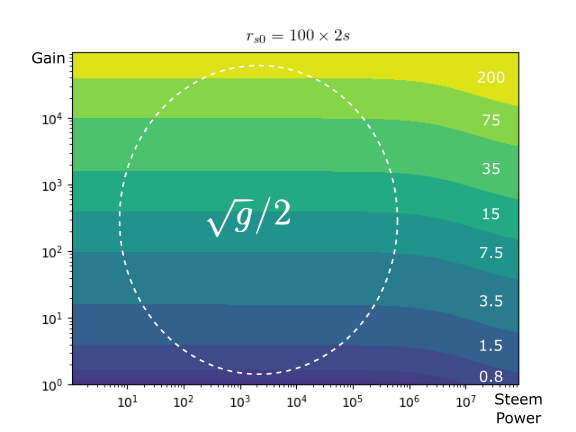
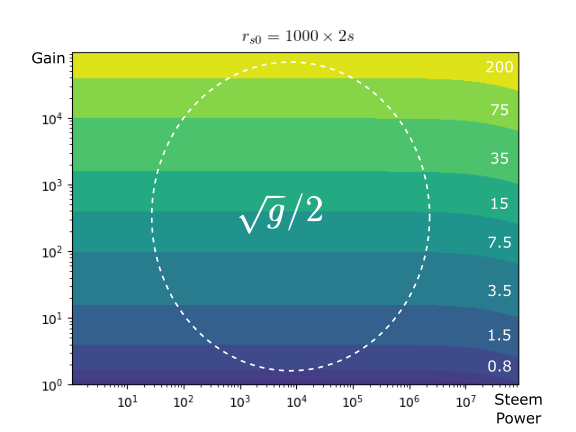
K in figures
The following figures show different values of K. In the x-axis is the vote translated to steem power (rshares generated with the manabar full), and in the y-axis is the gain g. The values of K are represented with colors. We see that the minimum value is 0.5, and the maximum depends on g (in the figures it is caped to 200).
Examples:
- The post is new (rs0=0), and you have 10 000 steem power. Then if there is no gain (g=1) the value of K is 0.5. But if the post receives more votes later and the gain is g=100 then K is around 2.
- The post is popular, rs0 much greater than the gap, then K is the square root of g divided by 2.
- When a big whale votes, with SP greater than 1 Million, then K is square root of g.
Votes before 5 minutes
An additional rule not mention before is that votes before 5 minutes are penalized proportional to the distance to 5 minutes, and this reward returns to the reward pool. For instance, one vote at time 0 is penalized in 100%, at 1 minute is 80%, at 2 minutes is 60%, at 3 minutes is 40%, at 4 minutes is 20%, and at 5 minutes there is no penalization.
This rule is present because bots have more advantage than humans by being able to vote instantly when a new post comes out. Then these minutes helps to reduce this disadvantage. The same happens with curators that vote to popular authors no matter the content, this period gives a chance to make a read before voting.
Downvotes
The rewards for curators presented before take in consideration no downvotes. The question is what happens if there are downvotes? how is the calculation in this case?
The downvotes do not have curation weight, and are not taken into account in the total weight W. Then, the individual payment for a single curator is
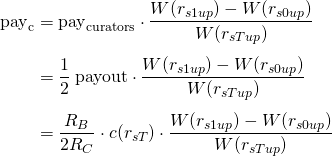
where the subindex "up" means only positive rshares. Let "d" be the relation between the final claims and the upvote claims:
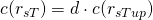
Then
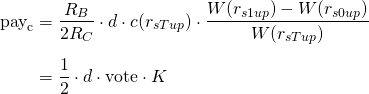
And the K is calculated using only the upvotes.
Example: Suppose that a post reach 400 steem. After that people start to downvote and the final payment is 300 steem. Then the downvotes represents -100 steem, and the value for "d" is 75%. Then the payments are calculated as if the total payout were 400 steem, and each payment is reduced by 25%.

The one minute timer on early votes was changed to five minutes.
Also I think the explanation given for the timer is incomplete but that's not really core to the post, which seems to be focusing more on the mechanics than the motivations.
Thanks for that. I changed it.
I would like to know your perspective about this rule.
It has a dual purpose. One is to slow down bots and the other is to reduce curation rewards on obviously high paid content (e.g. authors who get highly voted every time) that doesn't require much curation effort (nor risk).
You are right. I added that, thanks.
The two functions during this early period - the square-root and the linear - result in complex behaviour that is probably the only interesting bit of feedback in the whole system. :-) It is also highly profitable.
Thanks for the update re 5 minutes too - been so busy on my own projects have not kept up.
This is so valuable, thank you! :)
Posted using Partiko Android
Amigo @jga como decimos en Venezuela te la comiste.
pero con respecto al tiempo votación en un lapso de 5 minutos, muchos de esos bots pueden ser programados para el minuto 6 o 7 e igual pueden ganar ganar. cierto?
Sí, de hecho es una buena práctica programarlos para votar a los 5 minutos.
El punto está en que ya habrán pasado 5 minutos en los que un humano común y corriente habrá tenido algo de tiempo de darle un vistazo antes de votar.
Congratulations @jga! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPVote for @Steemitboard as a witness to get one more award and increased upvotes!
This makes me feel like in math class again... 😐....