How to optimize your upvote (mathematical analysis)

Do you know how much you get reward for curation? Should I vote for a post in trending? vote an unpopular post? How much does it matter? and on the other hand, how much does my steem power intervene in my curation? How to act with the rule of 30 minutes? Should I vote at 20, 25, 27?
There are many questions about curation. Do you want a better performance in this issue? This post will show you all the answers. We will see some maths here, but don't worry, if it is complicated for you just jump to the summary where you will find the main points to follow.
The formula of curation
In my last post we found the formula of curation:
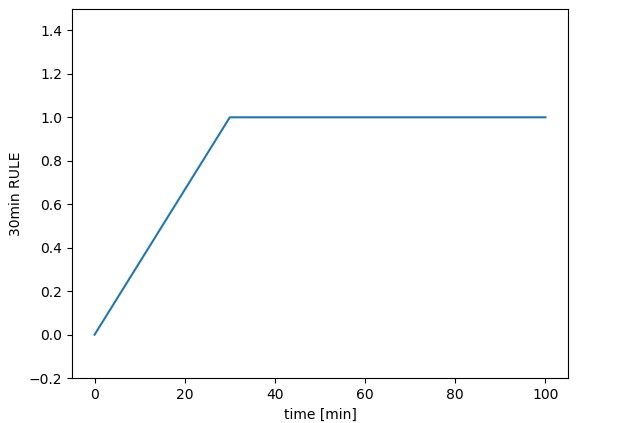
P0 is the payout before you vote, P1 is the payout after you vote, v is the worth of your vote, PT is the payout after 7 days, and t is a value between 0 and 1 in function to the rule of 30 minutes (if you vote right after the publication then it is 0, if you vote at 30 minutes then it is 1, in the middle the value is proportional to the time, and after 30 min it continues being 1).
Note: On steem, the formula to calculate the square root is not exact but approximate, to be able to make operations fast. Then the above calculations could differ a bit from the reality.
Let's see an example: Your vote is worth in $0.24. Then you vote a post worth in $5.00 (after 30 min). How much you will receive if that post after 7 days grows to $50?
But this value must be transformed into STEEM. If 1 Steem is worth in $5, then
Then you will receive 0.018 Steem Power. It is easy to calculate, but we need to go into more detail about the implications of this formula.
Rewriting the formula
Let's rewrite this formula in terms of the worth of your vote. Suppose that your vote is k times the payout P1, and the final payout is s times (scale) the payout P1:
For instance, if you are the first voter, then k=1 because there is no previous payout and therefore your vote is the total payout, P1 = v. But if you are late in your vote (P0 is big) and your are a minnow (v small), then k will be near 0.
As you can see k is a constant between 0 and 1, and defines some characteristics of your vote with respect of the timing and the popularity of a post.
With some calculations we get:
Including all this in the formula we get:
We can group the first fraction in a big K:
Then, rewriting we find this:
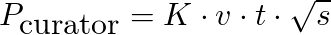
The value of K
But, what is the meaning of the big K? It represents the transformation of k into money. As we saw earlier, k is a value between 0 and 1. Let's see the range of values for K.
This is more difficult, we need to apply the L'Hopital's rule
Wow, then K is a value that goes from 1/8 (when you vote later) to 1/4 (when you are earlier voter). The following graph shows a representation of this value. The x-axis corresponds to the ratio v/P0. For instance, suppose before upvote the payout is P0 = $5 and the worth of the vote is v = $0.5, then the ratio v/P0 is 0.1, which corresponds in the graph to K=0.128.
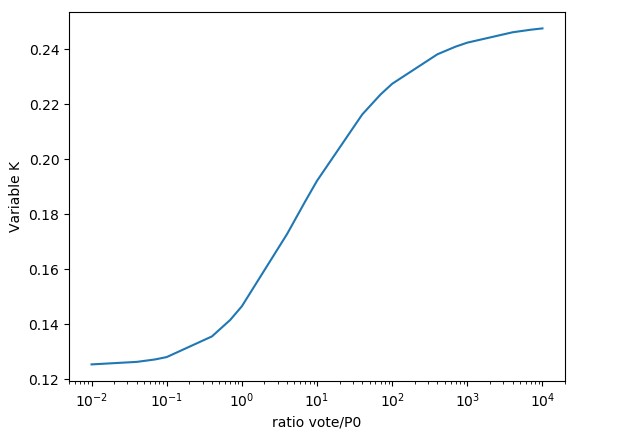
- If we want to achieve a value near to 0.25 the vote
vmust be several times higher thanP0, about 1000 times higher. Here we have two options: 1) Be the first voter, in this caseP0=0and thereforevis infinitely larger. 2) Be a whale and be an earlier voter: SinceP0is small andvis very large, the proportion could be reached. - If our vote
vhas the same value of the payoutP0, thenv/P0 = 1, andK=0.146. - While our vote
vis less than the payoutP0the value ofKwill approach 0.125, its minimum.
Examples of curation
Let's see some examples.
Example 1: Minnow votes early for a post that becomes trending
Suppose a vote of a minnow (worth in $0.10) and she is the first voter (after 30 min). What is the reward if the post reaches $5 after a week? Look that $5 is 50 times $0.1.
She will get more than worth of her vote. This would be an ideal case, but difficult to achieve. Look, she is first, which is good, the vote is after 30 minutes (the 30-min rule is all for she), and it grows 50 times!!. One important conclusion is that your rewards increase with the square root of the scale. As the payout increases 50 times your payout increases sqrt(50) times (that is 7.07 times).
Example 2: Whale votes a trending post
Suppose a whale that gives a vote worth in $40 to a trending post which has $460, and the post doesn't get much more after that. In this case, when he votes the post reaches $500, then k=40/500=0.08, and K=0.1276 (near to 1/8 because he votes late). His payment will be:
What we can conclude here is that your Steem Power is very important. The more you have the more you receive in a proportional way. In the example, the curator received one eighth of his vote.
Example 3: Minnow votes a trending post
Suppose the same as before but the worth of the vote is $0.10. In this case the total payout will be $460.10, then k=0.1/460.1=0.000217, and K=0.125. His payment will be:
The result is almost the same as before, the curator receives one eight of his vote. Look that we found that K is almost the same in both cases. Then we can conclude that this value is near to 1/8 when you upvote a post in trending no matter if you are a minnow or a whale. This is an amazing simplification, since by definition K depends on the value of the vote.
Example 4: Upvote to an unpopular post
Suppose a vote worth in $1.00 applied to a post that has $0.03. The vote is after 30 minutes. The post is unpopular and after a week it only reaches $1.72. What is the reward for the curator? Here we found that k=1/1.03=0.97, and K=0.2135. And s=1.72/1.03=1.67
He is not the first voter but the worth of his vote is much higher than the initial payment, then K is higher similar to the example 1.
Example 5: Minimum reward
Suppose you vote late and the post does not grow after the upvote. Here K takes its minimum value, and s is 1.
Many people thinks that if you upvote a trending post worth in $2500 you will receive less than other post worth in $400. This is not true. The above calculation clearly shows us that there is a minimum no matter the value of the post!! It depends only on the worth of the vote.
Beating the rule 30-min
In the previous examples we always assumed that the vote was made after 30 minutes, where the value of t is 1. Here we will see what happens when you upvote before and what is the best time to do it.
Let's define some values:
When the curator upvotes the total payment is P1. This payment scales s30 times and reaches the payment P30 at 30 minutes. On the other hand we use the same s to define the scale until a week, the final payment PT. And from 30-min to a week the post scales c times. In this order of ideas:
The question is: Should I wait until 30 minutes? or is it better to upvote before? First lets see the curator's payment if the he upvotes at 30 min, that is s=c and t=1:
On the other hand, if he upvotes before we have:
Where Dt is the time of the vote in minutes. Now, let's compare these 2 results. We will assume that the value of K is close in both cases.
Conclusion: If we believe that the post will grow greater than 900/Dt² then it is better upvote before!! Examples:
- A post has $99 at 10 minutes. With your upvote it could reach $100. Some calculations:
900/10²=9. And$100(9)=$900. The question is: Do you think the post could reach $900 or more at 30 minutes? if the answer is yes then upvote now, if not then wait. - A post has $9.9 at 15 minutes. With your upvote it could reach $10. Calcs
900/15²=4. And$10(4)=$40. Do you think the post could reach $40 or more at 30 minutes? if yes upvote now, if not then wait. - A post has $69 at 25 minutes. With your upvote it could reach $70.
900/25²=1.44. And$70(1.44)=$100.8. Do you think that in the next 5 minutes the post could reach $100.8 or more? if yes upvote now, if not then wait.
It's easy, no?
Summary
Your rewards for curation can be calculated using this formula:
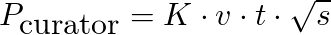
where:
Kis a value between 0.125 (if you vote late) and 0.250 (if you are the first voter). It is very difficult achieve 0.25 or similar if you are not the first (you need to be a whale), and it is easy achieve a value near to 0.125. This depends on your steem power and the moment you vote.vis the worth of your vote. You can calculate it using steemnow.com.tis the 30min-rule, a value between 0 and 1. If you vote at 0 minutes of publication it is 0. At 10 minutes it is 0.33. At 20 minutes it is 0.66. At 30 minutes it is 1. After 30 min it continues in 1.sis the growth of the post after your vote. If the post has $20 just after your vote, and after a week it reaches $100, thens=100/20=5.
This payout is transformed into Steem Power, then it is divided by the price of steem.
Some conclusions
- Rewards increase with the square root of the growth scale of the post.
- Rewards increase linearly with the worth of the vote. The more steem power you have the more profits you will have.
- If you vote late a trending post the reward is
v/8no matter the value of the post. - If you vote after 30 min, and you are the first voter you will receive a minimum of
v/4, no matter if the post is popular or not. - At 30 minutes you get all the reward, but if you vote before the gains decrease with respect to time. The rule to upvote before 30 minutes is: If you believe that the post will grow greater than
900/Dt²times (whereDtis the time in minutes) then it is better upvote.
I hope you enjoyed it as much as I enjoyed writing and scrutinizing the reward system.

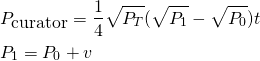
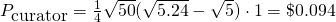
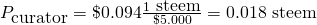
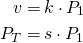
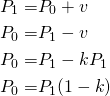
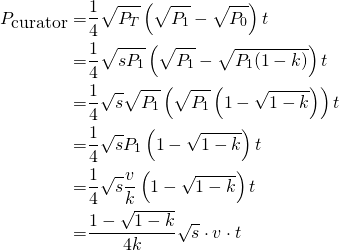
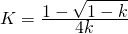
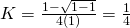
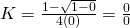
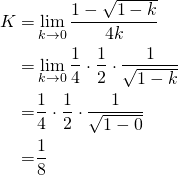
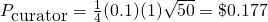
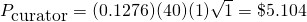
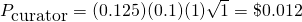
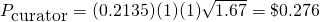
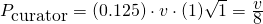
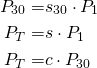
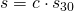
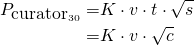
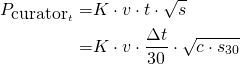

Wow, I am impressed. Congrats!
You should repost this in a form of the tutorial at https://utopian.io/.
Do you think that this is possible?
When I write this post I had doubts about whether to publish it in utopian or not since it had to do with mathematics mainly and not with software as such, I do not know if I was wrong in it
I think this could count as documentation.
The rules say that only pull requests "merged" are accepted.
I sent my pull request to steemit/steem but they responded me that this documentation is for the whitepaper, another repository. Then I sent my pull request to the whitepaper but the repository is not very active, I'm waiting they reply. I will wait :)
Thanks
You can try it as tutorial.
Super very good work man!
thx for the in-depth analysis, wow seems a bit more complicated than I thought ;) I will continue to upvote favorite stuff without thinking too much about the formula ;)
Thank you very much
Excelente trabajo, @jga . Tendré que leerlo detenidamente.
Cualquier sugerencia, pregunta, corrección, o aclaración bienvenida sea. Un saludo.
Welcome to Steem.center, thanks for registering! A link to your post was included in the wiki article about Upvote. Feel free to edit, change or add any information you want. Thanks and good luck again!
thank you very much. I started with some changes and a new page :)
https://www.steem.center/index.php?title=Rewards
Thank you for this very good post! You explained everything very well and it's easy to understand all the concepts.
Thank you very much
Muy buen trabajo mi amigo, se ve que te esforzaste, este post merece estar en tendencia. Bueno espero que te sirva de algo mi follow y mi upvote amigo. Sigue así
Wow ahora que me acuerdo mientras voy escribiendo este comentario y creo que te he visto en algun video de youtube hace tiempo, no se si estoy loco pero bueno jajajaja
¡¡Feliz año 2018 y saludos!!
Gracias @miguelb. Sí, en realidad es un post de muchas horas de investigación, recopilación y análisis. Gracias por el comentario. Y sí, yo estoy en un par de videos en youtube, por ejemplo en uno que hizo @anahilarski de un meeting de steemit aquí en Panamá.
Un saludo.
WOW. Excelente work. I was doing a lot of searching to find a formula for rewards and you gave them to me with analysis and examples.
Yes. This was the idea. I'm glad it's helpful.
Some amazing math there my friend.
Thank you for coming here and for your upvote @kus-knee!! :)
Amazing math work, thank you, i can understand very well now how curation works.. Stay blessed.