Composición de Funciones
Saludos a toda la comunidad científica y académica de Steemit, nuevamente nos encontramos para continuar con el estudio de las Funciones, para lo cual se presentará a continuación el saber matemático vinculado con éstas, a saber, la Composición de Funciones, el cual se detallará fundamentalmente desde las perspectivas teórica, demostrativa, gráfica, así como el desarrollo de ejemplos que potenciarán la posibilidad de comprensión de los lectores y estudiantes de esta comunidad.
Se invita a los lectores a dar un lectura previa sobre la composición de relaciones - ver aquí – en tanto que el referido apartado se considera como conocimiento previo que facilitará el estudio de los saberes que se presentarán en esta publicación. Recordemos que toda función es una relación, aunque no toda relación es función, en este sentido, lo relativo a la temática de relaciones binarias es considerado saber previo de gran importancia al tópico de las Funciones. Comencemos.
Así como se estudió en una publicación anterior - ver aquí – la posibilidad de componer relaciones, en una perspectiva similar también puede ocurrir con las funciones, con la diferencia de que en ésta oportunidad al realizar una composición de funciones estamos conscientes de que las mismas deben cumplir (o cumplen dependiendo del escenario problemático planteado) con las condiciones de
- Existencia de Imagen
- Unicidad de Imagen
Y por ende, la función compuesta de igual manera debe verificar tales condiciones. Ahora procedamos con la definición formal, esto es
Sean las funciones f:A⟶B y g:B⟶C se define la función compuesta de la siguiente manera
La notación g∘f se lee f compuesta con g y representa a la función compuesta de f con g. De igual forma es posible determinar f∘g que identifica a la función compuesta de g con f, y su expresión matemática es
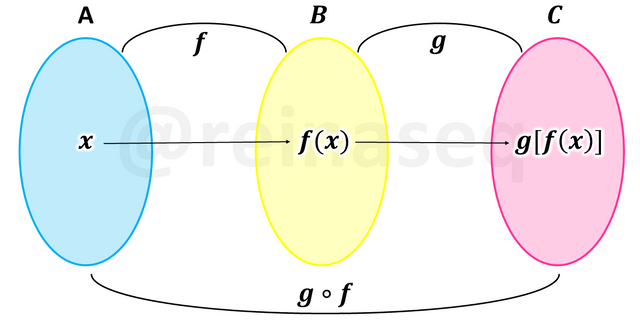
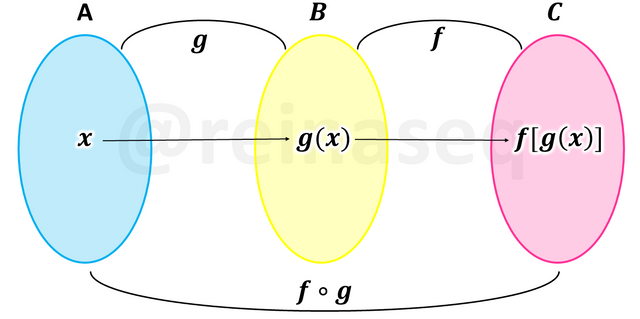
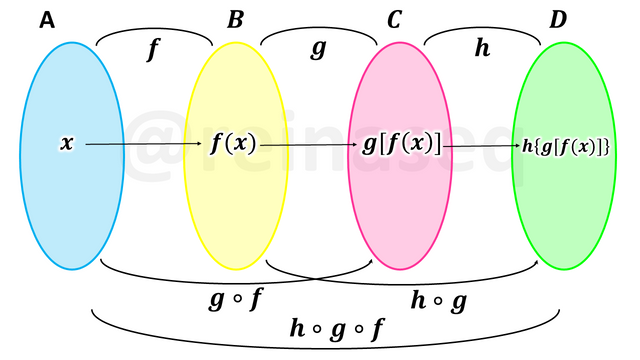
Visualizando en un Diagrama de Venn tenemos
Cabe destacar que las funciones compuestas g∘f y f∘g en general no coinciden lo que implica que no verifican la propiedad conmutativa.
- Ejemplo
Dadas las funciones
f:R⟶R/f(x) =4x+3
g:R⟶R/g(x) =x2
Determinar: g∘f y f∘g
Solución
Para precisar g∘f aplicamos la definición, es decir
g∘f:R⟶R/(g∘f)(x)=g[f(x)]
Al analizar los dominios y codominios de las funciones f y g es claro que la compuesta de igual modo estará definida en el conjunto de los números reales R, esto quiere decir que nos falta identificar la expresión matemática que la define, por lo cual procedemos como sigue
g[f(x)]=g(4x+3), por definición de f
g[f(x)]=(4x+3)2, por definición de g
g[f(x)]=(4x+3).(4x+3), por definición de potenciación en el conjunto de los números reales R
g[f(x)]=4x2+24x+9, por definición de potenciación en el conjunto de los números reales R
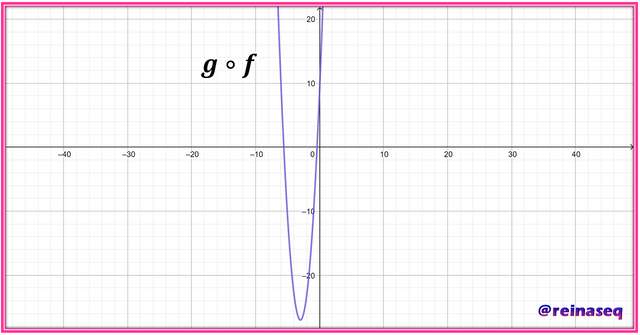
∴g∘f:R⟶R/g[f(x)]=4x2+24x+9
Visualizando el gráfico cartesiano tenemos
Ahora procedamos a determinar f∘g, la cual al igual que la anterior estará definida en el conjunto de los números reales R, esto es
f∘g:R⟶R/f[g(x)]
A continuación determinamos la expresión matemática que la define
f[g(x)]=f(x2), por definición de g
f[g(x)]=4x2+3, por definición de f
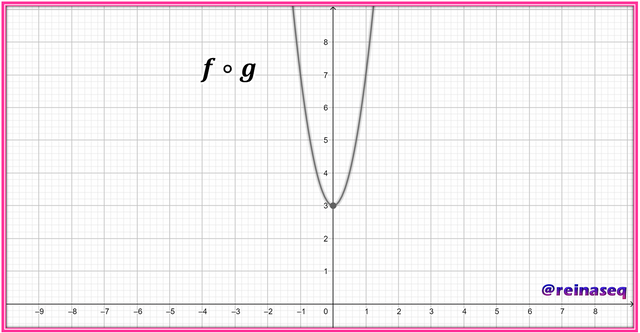
∴f∘g:R⟶R/f[g(x)]=4x2+3
Graficando tenemos
Como se puede observar, tanto por las expresiones algebraicas resultantes para ambas funciones compuestas como por sus gráficas respectivas, se ratifica que g∘f ≠ f∘g, esto es, no se cumple la propiedad conmutativa.
- Igualdad de Funciones
Sean las funciones f:A⟶B y g:A⟶B se dice que éstas son iguales si y sólo si son iguales sus imágenes respectivas para todo elemento que pertenezca al conjunto de llegada. Simbólicamente es.

- Asociatividad
Para esta propiedad se requieren al menos tres funcione para poder definirla, a saber, f:A⟶B, g:B⟶C y h:C⟶D
Es de hacer notar que los dominios y codominios de ambas funciones compuestas son (h∘g)∘f:A⟶D y h∘(g∘f):A⟶D, los cuales pueden ser visualizados en el siguiente Diagrama de Venn
Ahora bien, para demostrar la asociatividad se debe considerar la definición de igualdad de funciones, por lo cual se deben desarrollar ambas imágenes y luego compararlas. Procedamos:
i ((h∘g)∘f)(x)=(h∘g)[f(x)], por definición de función compuesta
=h{g[f(x)]}, por definición de función compuesta
ii (h∘(g∘f))(x)=h[(g∘f)(x)], por definición de función compuesta
=h{g[f(x)]}, por definición de función compuesta
∴ Por i y ii se demuestra que (h∘g)∘f=h∘(g∘f), por definición de Igualdad de Funciones∎
- Composición de Funciones Inyectivas
Sean las funciones f:A⟶B y g:B⟶C se dice que si éstas son inyectivas entonces la función compuesta g∘f:A⟶C también lo es. En símbolos.
Demostración
En esta comprobación debemos considerar las definiciones de función compuesta y función inyectiva. En este sentido, recordamos que en el caso de la inyectividad se establece por definición que si las imágenes son iguales entonces los elementos de los cuales proceden también lo son, por lo cual partiremos de la igualdad de las imágenes de los elementos a y b mediante la función compuesta g∘f y veremos que sucede.
(g∘f)(a)=(g∘f)(b)⟹g[f(a)]=g[f(b)], por definición de función compuesta
⟹f(a)=f(b), por ser g inyectiva
⟹a=b, por ser f inyectiva
∴ Se demuestra que Si f:A⟶B∧g:A⟶B son inyectivas⟹g∘f es inyectiva∎
- Composición de Funciones Sobreyectivas
Sean las funciones f:A⟶B y g:B⟶C si las mismas son sobreyectivas entonces la función compuesta g∘f:A⟶C también es sobreyectiva. En notación simbólica.
Demostración
Al igual que en la comprobación debemos considerar las definiciones de función compuesta y en este caso función sobreyectiva. En este sentido, se debe demostrar que para todo elemento del conjunto de llegada existe un elemento en el conjunto de partida de manera que la imagen del elemento del conjunto de partida a través de la función compuesta g∘f es igual al elemento en el conjunto de llegada.
Simbólicamente lo que se quiere demostrar es que ∀c∈C,∃a∈A/(g∘f)(a) =c, por lo cual procederemos como sigue:
Se sabe que la función g:B⟶C es sobreyectiva, entonces
∀c∈C,∃b∈B/g(b) =c, (I)
Adicionalmente también se conoce que la función f:A⟶B es sobreyectiva, por lo cual
∀b∈B,∃a∈A/f(a) =b, (II)
Como se puede observar las funciones f:A⟶B y g:B⟶C tienen en común el elemento b∈B y por la expresión (II) sabemos que f(a)=b luego la expresión (I) queda representada como sigue
g(b)=c⟹g[f(a)]=c, por la anterior deducción
⟹(g∘f)(a)=c,a∈A∧c∈C, por definición de función compuesta
∴Se demuestra que Si f:A⟶B∧g:A⟶B son sobreyectivas⟹g∘f es sobreyectiva∎
- Composición de Funciones Biyectivas
Sean las funciones f:A⟶B y g:B⟶C se tiene que si éstas son biyectivas entonces la función compuesta g∘f:A⟶C es biyectiva. Simbólicamente.
Para esta demostración particular se procede de manera similar que en las anteriores propiedades, salvo que, la hipótesis a considerar es la biyectividad de las funciones f:A⟶B y g:B⟶C, y como sabemos, si una función es biyectiva es porque verifica de forma simultánea la inyectividad y sobreyectividad. En esta comprobación, deben a su vez desarrollarse las comprobaciones de inyectividad y sobreyectividad, las cuales se dejarán sugeridas a los lectores a manera de ejercitación.
Una vez que se realizan las verificaciones sugeridas se tiene que
∴Se demuestra que Si f:A⟶B∧g:A⟶B son biyectivas⟹g∘f es biyectiva, por definición de función biyectiva∎
Mediante la presente publicación hemos logrado estudiar los aspectos concernientes a la composición de funciones o función compuesta, presentando sus detalles teóricos, gráficos, prácticos y demostrativos. Como se trata de mostrar la visión algebraica se procuró ir más allá de los planteamientos tradicionales del tema que generalmente se enfocan en lo teórico y práctico. El interés del abordaje mostrado en este post tiene que ver con la búsqueda de relevancia de los aspectos formales de éste y otros conceptos estudiados previamente, los cuales facilitan en gran modo la comprensión de los saberes compartidos, en tanto que se va más allá de los razonamientos y expresiones que comúnmente se encuentran en los textos.
En los procesos de formación de la ciencia la especificidad y el detalle son fundamentales si se pretende fortalecer a la comunidad científica, nada en la ciencia está sobreentendido, es necesario facilitar el enfoque del detalle lo cual conlleva de forma favorable al desarrollo de la curiosidad y creatividad.
En las próximas publicaciones, se dará continuidad al estudio de las funciones abordando un nuevo tópico inherente a las mismas, nos leemos en el siguiente post, saludos y éxitos para todos los lectores y académicos de esta comunidad.

¿Qué misterios de la naturaleza no pueden ser comprendidos con el apoyo de la Matemática? – Reina Sequera
¿Qué misterios de la naturaleza no pueden ser comprendidos con el apoyo de la Matemática? – Reina Sequera

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia diseñadas en el editor de presentaciones Microsoft Powerpoint 2013, ajustadas y recortadas en Paint.
Los gráficos cartesianos fueron diseñados por @reinaseq mediante el software Geogebra en Línea
Publicaciones Relacionadas





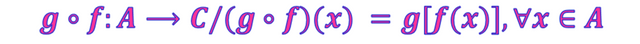
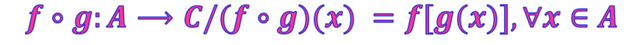
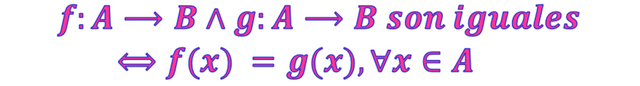
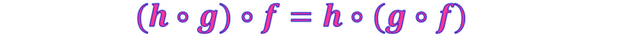
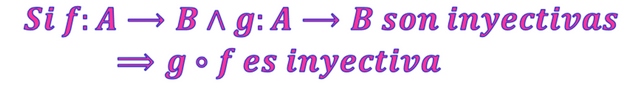
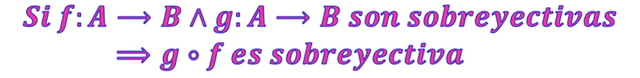
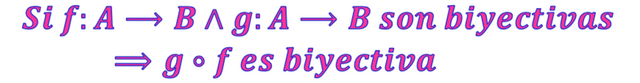

I upvoted your post.
Keep steeming for a better tomorrow.
@Acknowledgement - God Bless
Posted using https://Steeming.com condenser site.
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Excelente y educativo artículo el que nos presentas, mi amiga @reinaseq, acerca de la composición de funciones. Muy bueno para dar una clase. Mis felicitaciones, su presentación tan buena hace que uno disfrute su lectura. Saludos.
Muchas gracias @tsoldovieri por valorar mi aporte, aprecio su generoso gesto, esa es precisamente la idea, que pueda ser utilizado como recurso educativo por la comunidad académica y científica de Steemit!! Abrazos fraternos!!
¡Felicidades, #proconocimiento te valoró!
Has sido reconocido(a) por tu buen post por el Comité de Arbitraje y Valoración del Proyecto Conocimiento @proconocimiento.
Apoyamos y valoramos tu esfuerzo...
Proyecto Conocimiento es parte de la comunidad @provenezuela.
Pioneros en la plataforma #steemit en el reconocimiento y valoración a la Producción Intelectual en habla hispana.