Una fórmula explícita para los números de Fibonacci
Los números de Fibonacci son una de las sucesiones más conocidas por el público general, hasta son mencionados en películas de Hollywood. Estos números tienen muchas aplicaciones en diversas ramas de la ciencia y también en el arte y arquitectura; ya que las proporciones involucradas en la noción de belleza, están relacionadas con estos números.
Si denotamos por fn el n-esimo número de Fibonacci, estos están definidos por la relación de recurrencia fn+2=fn+1+fn, donde n es un entero no-negativo, y las semillas, o datos iniciales son f0=0 y f1=1.
Nos gustaría tener una fórmula cerrada o explícita para fn, es decir una que no involucre recurrencia. La respuesta se conoce como la Fórmula de Binet. Se le ha dado el nombre del matemático Francés Jacques Philippe Marie Binet (1786-1856), quien el 1843 la publicó. Aunque ya era conocida por Abraham de Moivre (1667-1754), Leonhard Euler (1707-1783) y Daniel Bernoulli (1700-1782).
La fórmula de Binet es:
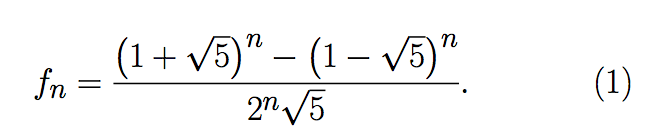
Sin embargo hay una manera más elegante de expresarla, usando la razón dorada ( o también llamada razón áurea). La denotamos por Φ:
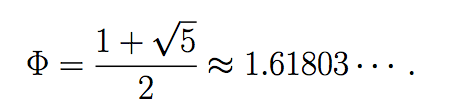
Recordemos que Φ es la raíz positiva del polinomio x2-x-1. Este polinomio está asociado a la relación de recurrencia de Fibonacci. Sea φ la otra raíz de es este polinomio.
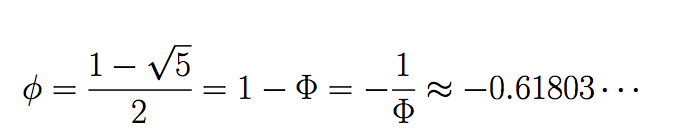
La fórmula (1) escrita en términos de Φ y φ es
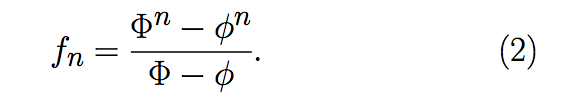
A continuación daremos una demostración de la fórmula de Binet.
Sea Zn=aΦn+bφn donde a y b son constantes. Mostraremos que Zn satisface la misma relación de recurrencia que la de los números de Fibonacci, es decir: Zn+2=Zn+1+Zn. Luego se encontrarán los valores de a y b tales que Z0=0 y Z1=1. De esta manera se demostrará la fórmula (2).
Como Φ y φ son raíces de la ecuación x2=x+1, las siguientes identidades se cumplen, para n entero no-negativo:
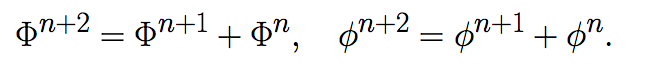
Por lo tanto:
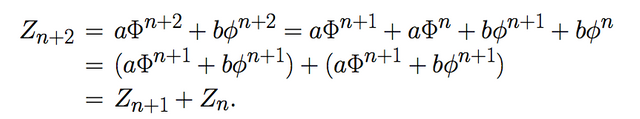
Si se establece que Z0=0 entonces se tiene a+b=0. Similarmente, si Z1=1 entonces aΦ+bφ=1. De esta manera obtenemos el sistema de ecuaciones:
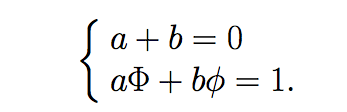
Su solución es:
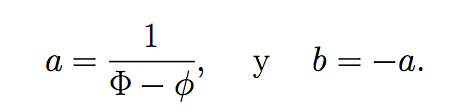
Por lo tanto Zn=fn, demostrando así la fórmula (2).
Referencias:
https://en.wikipedia.org/wiki/Fibonacci_number#Closed-form_expression
http://mathworld.wolfram.com/BinetsFibonacciNumberFormula.html
https://en.wikipedia.org/wiki/Jacques_Philippe_Marie_Binet
T. Koshy, Fibonacci and Lucas Numbers with Applications, Wiley-Interscience, 2001.
Muy interesante amigo, no sabia que se podía sacar como factor común la raíz de 5 de la ecuación de Binet y mucho menos que era la ecuación áurea jeje, siempre me ha gustado mas la practica de las matemáticas que la teoria
Saludos
Me alegra que el post haya sido de tu agrado. Gracias por el comentario.
Gracias por compartir este post sobre la sucesión de Fibonacci. El estudio de las sucesiones es uno de mis campos preferidos de las Matemáticas.
Te felicito por lo conciso y elegante de la demostración que presentas.
Mencionaste lo siguiente:
En efecto, tal polinomio es el llamado "polinomio característico" de la relación de recurrencia de la sucesión de Fibonacci.
Tengo en mente (desde hace semanas) postear sobre el procedimiento para construir los polinomios característicos de las ecuaciones de recurrencia y a partir de sus raíces hallar la fórmula general o explícita. Tal vez te interese.
Cualquier relación de recurrencia lineal, tiene asociada un polinomio. El cual tiene diversos nombres en la literatura, por ejemplo asociado, auxiliar o característico. Este último nombre se debe a que es polinomio característico de la matriz asociada a la relación de recurrencia.
Se puede escribir una fórmula explicita del término general de la sucesión, usando las raíces de su polinomio. En la literatura a esta formula se le llama la fórmula de Binet de la relación de recurrencia.
El caso de Fibonacci, es el más conocido, fue el primero en expresarse y el más elegante.
Cuando la relación de recurrencia es de orden mayor a dos. La correspondiente fórmula de Binet es más complicada.
Gracias por el comentario.
i love mathematics and numbers
Thank you.
todo un maestro en matematicas, imagino que disfrutaba esas clases... para mi siempre fue dificil, saludos amigo, interesante su post
La sucesión de Fibonacci es un tema que me llamo mucho la atención desde el momento que me hablaron por primera vez sobre ella. De hecho es tanto así, que siempre que puedo intento buscar esta sucesión en cada cosa que me encuentro, podria decir que me obsesiona jaja. Como curiosidad sobre lo que dijiste al comienzo acerca de que es una de las sucesiones mas conocidas en la cultura pop, me tomo la libertad de mencionar que en el videojuego Owlboy existen dos personajes que hacen clara referencia a este matemático. El nombre de los personajes son Fi y Bonacci, una clara referencia que es dificil no darse cuenta de ella. Saludos.
No sabía que ese juego hacía esta referencia.
La película el Código da Vinci menciona a esta sucesión.
Gracias por el comentario.
Rayos me hiciste recordarme de mis estudios de ingeniería!
La idea es divulgar conocimientos básicos e interesantes de la matemática.
Good work
Felicidades!

La sucesión de Fibonacci es un tema que me llamo mucho la atención desde el momento que me hablaron por primera vez sobre ella. De hecho es tanto así, que siempre que puedo intento buscar esta sucesión en cada cosa que me encuentro, podria decir que me obsesiona jaja. Como curiosidad sobre lo que dijiste al comienzo acerca de que es una de las sucesiones mas conocidas en la cultura pop, me tomo la libertad de mencionar que en el videojuego Owlboy existen dos personajes que hacen clara referencia a este matemático. El nombre de los personajes son Fi y Bonacci, una clara referencia que es dificil no darse cuenta de ella. Saludos.
Gracias por ayudarnos a fortalecer la cultura matemática. Dios no sólo es el gran arquitecto. Él habla en todas sus obras con matemáticas. Y de alguna manera, este número está asociado a la perfección y a lo bello. Saludos