Saludos queridos lectores, bienvenidos nuevamente. En está oportunidad hablaremos un poco de una de las aplicaciones de la Transformada de Laplace para resolver Ecuaciones Diferenciales Ordinarias (EDO), en específico aquí mostraremos como usarlas para resolver Ecuaciones Diferenciales Ordinarias de segundo orden con coeficientes constantes. La misma está dirigida al público en general, pero con atención especial a estudiantes universitarios de ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

La transformada de Laplace

El Matemático Francés Pierre-Simon Laplace (1749-1827), además de dedicarse a las matemáticas, también fue físico y astrónomo, mientras seguía sus estudios en estadística, sentó las bases de la teoría analítica de las probabilidades, y fue cuando introdujo el concepto de la Transformada de Laplace.

De estamanera, la podemos definir como sigue:

La Transformada de Laplace, satisface las siguientes propiedades:

1. Linealidad:
   
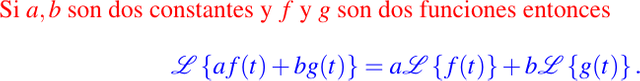
2. 1er Traslación:
   
3. 2da Traslación:
   
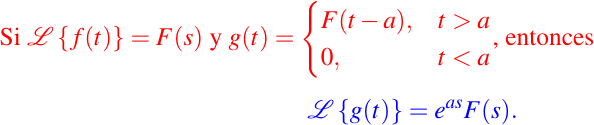
4. Cambio de Escala:
   
5. Desplazamiento temporal:
   
6. Derivación:
   
7. Integración:
   
8. Dualidad:
   
   
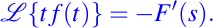
9. Desplazamiento, potencia n--ésima:
   
   
10. División por t:
    
11. Función con periodo T:
    
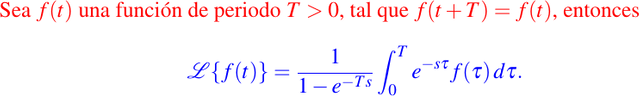
12. Teorema del valor inicial:
    
13. Teorema del valor final:
    

---

---

Tabla de las transformadas de Laplace elementales

A continuación, presentaremos una tabla donde podrán encontrar las Transformadas de Laplace para funciones de una sola variable. Es de hacer notar y resaltar como ya lo dijimos anteriormente, que la transformada de Laplace es un operador lineal, con respecto a la suma, y con respecto a la multiplicación por escalares, lo cual podemos expresar de la siguiente manera:

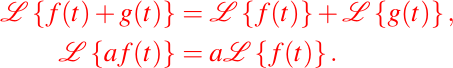
Luego, la tabla es:

---

---

Transformada inversa de Laplace

Cada vez que en Matemáticas definimos una operación, ésta siempre tiene definida su operación inversa, por ejemplo, las operaciones más básicas que conocemos, tenemos: la suma y la resta, el producto y el cociente, la derivada y la anti-derivada o integración, etc. Así podemos continuar la lista.

Luego, la transformada de Laplace de una función F(s) tiene su transformada inversa de Laplace, la cuál es una función f(t) que satisface lo siguiente:

donde la L cursiva, es la transformada de Laplace. Es bueno resaltar, que el operador de la transformada de Laplace y su inversa satisfacen un número de propiedades que las hacen útiles para el análisis de sistemas dinámicos lineales.

Ahora podemos dar una fórmula para la transformada inversa de Laplace, esta fórmula es conocida también como la integral de Bromwich, integral de Fourier-Mellin o fórmula inversa de Mellin, la cuál está dada como sigue:

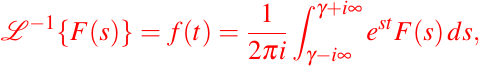
donde la integración se realiza a lo largo de la línea vertical

en el plano complejo tal que gamma es mayor que la parte real de todas las singularidades de F(s).

---

---

Tabla de las transformadas inversa de Laplace elementales

---

---

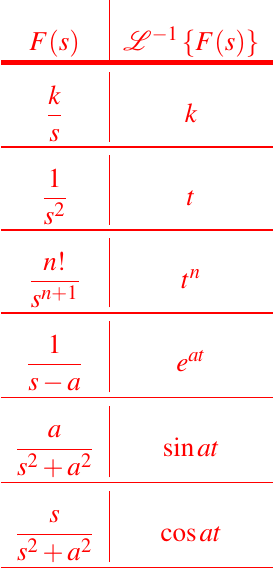
Aplicación de las transformadas de Laplace a Problemas con Valores Iniciales (PVI)

Una de las aplicaciones del Operador de la transformada de Laplace es para resolver problemas de valores iniciales (PVI), en particular trataremos como resolver ecuaciones diferenciales ordinarias de segundo orden con coeficientes constantes.

Para ello, supongamos que deseamos resolver la ecuación diferencial de segundo orden con coeficientes constantes siguiente:

sujetas a las condiciones iniciales (o de frontera):


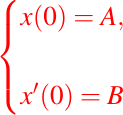
donde A y B son constantes dadas. Ahora, como el operador de la transformada de Laplace, es lineal con respecto a la suma y al producto por escalar, entonces al aplicarle el operador de la transformada de Laplace a la ecuación anterior, y aplicando la propiedad de linealidad del operador tenemos:


como podemos observar esta ecuación involucra las transformadas de la primera derivada y la segunda derivada de una función desconocida x(t).

Luego, utilizando las propiedades de la transformada de Laplace, tenemos lo siguiente:

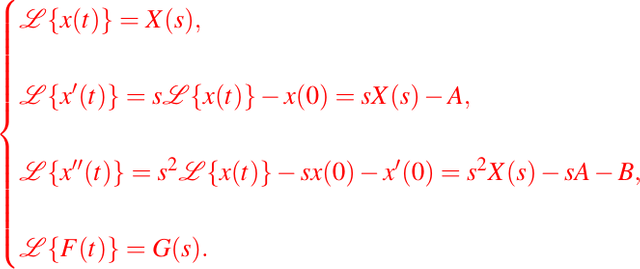
Entonces la ecuación transformada que nos queda es:


simplificando nos queda:


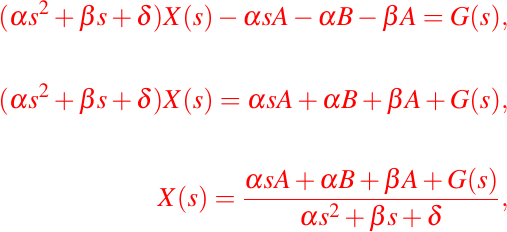
Luego, como necesitamos hallar x(t), debemos a la ecuación anterior aplicar la transformada inversa de Laplace convenientemente.

---

---

Ejemplo: Hallar la solución del problema de valores iniciales siguiente:

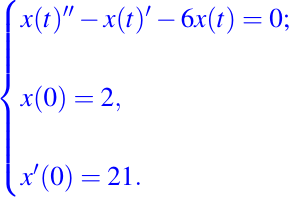
Para hallar la solución de la EDO de segundo grado con coeficientes constantes, usando la transformada de Laplace al PVI dado, tenemos:

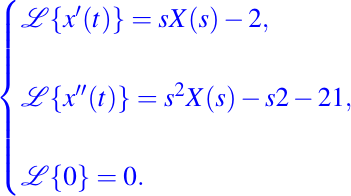
De esta manera, la ecuación transformada es

si simplificamos obtenemos

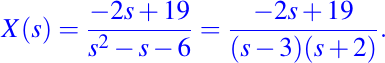
Así, luego de factorizar el denominador, debemos tratar de poder obtener un cociente equivalente al que tenemos con el objetivo de poder aplicar alguna de las transformadas inversas de Laplace elementales dadas, para ello debemos aplicar al cociente de la derecha un proceso conocido como fracciones parciales, el cuál consiste es hallar dos valores A y B tales que se satisfaga lo siguiente:

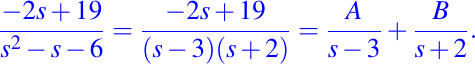
por lo tanto, los valores de A y B son 13/5 y -23/5 respectivamente, sustituyendo tenemos entonces:

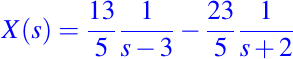
Luego, al aplicar la transformada inversa para hallar x(t) obtenemos:

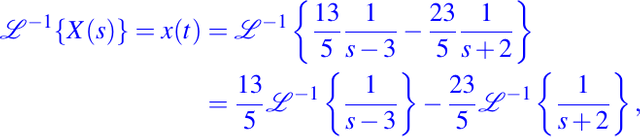
revisando la tabla de transformadas inversas de Laplace elementales tenemos que la solución al problema esta dada por:

---

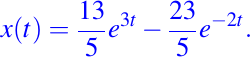
Queridos amigos y lectores, espero hayan disfrutado y aprendido una de las aplicaciones de la Transformada de Laplace para resolver problemas de valores iniciales. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la computación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias.

• Holbrook, James G. Transformadas de Laplace. 1972.
• Borda, Alberto Gutiérrez. Transformada de Laplace. Vol. 1 y 2. 2004.
• Zill, Dennis G. Ecuaciones diferenciales. International Thomson Editores. México. 1997.

---

_{Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.}