The Coastline paradox. How do you measure a coastline?
Do you believe that your country has a fixed, measurable and definite length of coast? Unless your country is land locked and the length is 0, you might be wrong. Measuring the edges where land meets water is much more difficult than first imagined and still causes different sources to suggest a variety of answers differing by thousands of kilometers. In the Year Book of Australia (1978) for example, we find a total coastal length of 36.735 km for Australia. A later publication of the Australian Handbook gives us a coastal length of 19.320 km. Although the difference is quite astonishing, these sources aren't necessarily all wrong, but this phenomenon is explained by the coastline paradox.

An innocent looking coastline, unaware of the complexity it causes.
The problem
Coastlines have already confused people since at least the 5th century B.C. When sailors were tasked to measure the coast of Sardinia they returned undecided on what the actual length was since measurements kept varying. You can suggest tides have something to do with it and the fact that coastlines keep changing due to erosion en deposition of material, but this does not explain the magnitude of the differences and the fact that the same problem occurs while measuring the borders of countries.
Koch's snowflake. An example of a fractal shape. The surface can be measured and has a defined size, the circumference is infinite.
In 1951 the English mathematician Lewis Fry Richardson conducted a study to figure out if border length was correlated with the likeliness of two countries to go to war. When gathering data he stumbled across the same difficulties the sailors encountered when measuring the coastline. Two countries could have measured the same border but come up with results sometimes twice as much as the other country. He further investigated this phenomenon and concluded that if it was possible to make your measurement unit small enough, the border would be effectively infinity long.
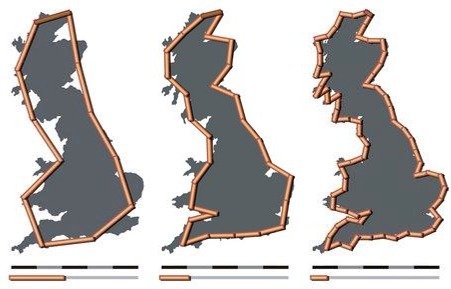
Visualization of the coastline paradox. Depending on the measurement unit, results can vary strongly.
The explanation
In 1956 another mathematician, Benoit Mandelbrot, continued researching this topic and published a paper "How long is the coast of Britain?". He concluded it to be impossible to measure the exact circumference of various other objects such as clouds, snowflakes or mountains. He created the concept of fractals, shapes that get more and more complex the closer you look at it. These fractals allow objects of a certain surface or volume to have a circumference of infinity.
Summarized, you could measure the coast with sticks of a kilometer, roughly estimating the shape and borders. When instead you use sticks of 1 mm, you will measure every little bay and crack in the rocks, resulting into a coastline that is significantly larger.
The solution
So that is the theory. Eventually people will have to find consensus on how to measure a coast line. These have to be known for many practical reasons. Many attempts have been made to come up with a standardized scale for measuring coastline length and until now still many standards are used.
One of the standards being used by the USA is defined where the distance between points equal the intervals of 30 latitude minutes as measured on a 1:200.000 scale map. But this is only an example and no uniform standard is commonly used.
Conclusion
There you have it, good luck trying to measure the coastline next time you are at the beach (If that is what you do when you are on vacation). It keeps amazing me how much complexity can be found in the world around us, even in places you wouldn't expect it.
So, next time you want to go to the beach, Don't worry about it being crowded. There are literally infinity more beaches!
I hope you liked what you read. If you have any questions or comments on the article/my writing, please let me know!
Sources
All images in this article were licensed for reuse.
https://www.atlasobscura.com/articles/why-its-impossible-to-know-a-coastlines-true-length
Mandelbrot, B. (1967). "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension". Science. 156 (3775): 636–638. doi:10.1126/science.156.3775.636.
http://awesci.com/coastline-paradox/
https://www.citymetric.com/horizons/how-long-coast-great-britain-it-depends-how-you-measure-it-2351
This post has been upvoted and picked by Daily Picked #35! Thank you for the cool and quality content. Keep going!
Don’t forget I’m not a robot. I explore, read, upvote and share manually ☺️
I like the way you wrote this. You can join the steemSTEM community and contact one of the mentors for the little help they can render. This post is nicely written but in my opinion, it's short and not explicit. Join the server here, contact a mentor for help, and you'd be good to go...
I have already been active in the steemSTEM community a bit. It is indeed not an entire scientific paper on the subject that goes into every detail of the matter, but the idea was to give a thorough introduction on the topic. Thanks for the feedback and have a nice day!
I think that there are practical/pragmatic solutions to this problem:
Surface tension will make any variation in the coastline no smaller than a few millimetres. So there is no need to go to the microscopic level to measure coastlines.
Due to wave action the coast has a certain fuzziness to it, always changing on a second by second basis. I think this fuzziness would make going lower than 10 metre resolution impractical.