Mathematical shapes known as fractals belong to the genius of the eminent scientist Benoit Mandelbrot. Most of his life he taught mathematics at Yale University, USA. In 1977 - 1982, Mandelbrot published the scientific works devoted to the study of "fractal geometry" or "geometry of nature", which was broken at seemingly random mathematical shapes on the constituent elements trapped upon closer inspection repetitive, and proved the existence of a certain model to copy. Opening Mandelbrot has had a significant impact in the development of physics, astronomy and biology. 

The Mandelbrot Set 

 

This is probably the most famous fractal. Here a rule f is given by the formula: f(z) = z2 + c where z and c are complex numbers. Each point on the line corresponds to a different real number, and every point on the plane — integrated. For complex numbers, as for valid, the operations of addition and multiplication. The Mandelbrot set is the black area in the illustrations, consists of all c such that the sequence of points z0 = 0; z1 = 02 + C = c z2 = c2 + c; z3 = (c2 + C)2 + C; ... not escapes to infinity, that is, all these points lie inside a circle with center at the origin. On the enlarged images is visible very complex structure of the set near the boundary. You can see the Islands, such a large black area. 

 

Image fishki.net 

Tree Of Pythagoras 

 

Is so called because each triplet of touching squares restricts a right triangle and get a picture, which often illustrate the Pythagorean theorem "Pythagorean pants on all sides are equal". It is clearly seen that all the wood is limited. If the large square unit, then the tree will fit in the rectangle 6 × 4. Then its area does not exceed 24. But on the other hand, each time is added to twice the triples of squares than in the previous year, and their linear sizes is √2 times smaller. 

Therefore, at each step, you will add the same square, which is equal to the area of the initial configuration, that is 2. It would seem, then the size of the tree must be infinite! But actually there is no contradiction, because pretty quickly the squares start to overlap, and the area grows not so quickly. It is still finite, but, apparently, still the exact value is unknown, and it is an open problem. 

 

Image giphy.com 

If you change the angles at the base of the triangle will get a slightly different tree shape. And at an angle of 60° all three squares are equal, and the tree will turn into a periodic pattern on the plane:

 

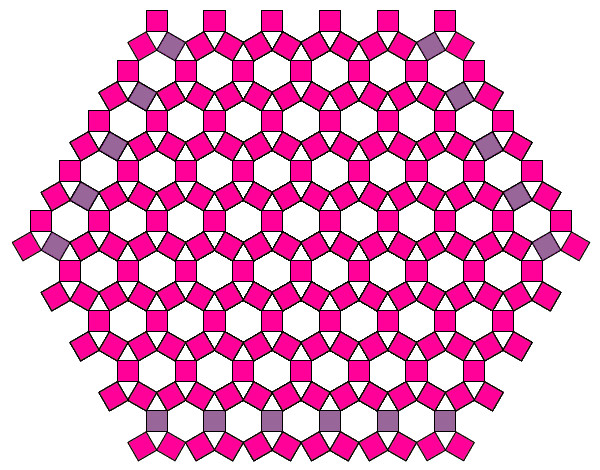
You can even replace the squares into rectangles. Then the tree will be more like real trees. And with some artistic treatment are rather realistic image: 

 

Curve Levi 

gif image elementy.ru 

Although this object was studied by the Italian Ernesto cesàro in 1906, its self-similarity and fractal properties researched in the 1930-ies the Frenchman Paul Pierre levy. The fractal dimension of the boundaries of the fractal is approximately equal to 1,9340... . But it is quite a complicated mathematical result and the exact value is unknown. For similarity with the letter "s" written in an ornate font, it is also called S-curve levy. If you look closely, you will notice that the curve of Levi is similar to the shape of the crown of the tree of Pythagoras. 

Options. 

Skosobochennoy curve is obtained if instead of the isosceles right triangle at each step to use any other triangle. The flash demonstrations you can experiment with different triangles and see what happens. Moving the slider can change the ratio of the legs of the triangle. Another variant of the S-curve Levi can build if you start from the cut, and with the letter P. Below shows the first three, the eighth and the eleventh steps of constructing this curve: 

 

 

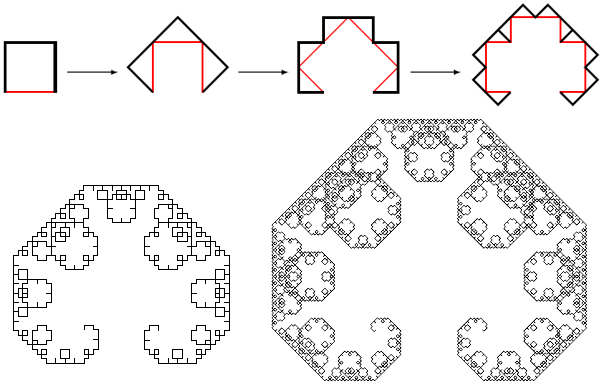
Many Julia Sets 

 

image pvsm.ru 

Any point z of the complex plane has its own character behavior remains finite, tends to infinity, accepts fixed values) at iterations of the function f(z), and the whole plane is divided into parts. At this point, lying on the borders of these parts, have this property: when an arbitrarily small displacement nature of their behavior changes dramatically (such points are called bifurcation points). The set of points with one particular type of behavior, and many bifurcation points often have fractal properties. This is the greatest Julia sets for the function f(z) 

Bubbles Halley 

These fractals are obtained, if the rules for building dynamic fractal to use Halley's formula for finding approximate values of roots of functions (see Halley's method). The formula is pretty bulky, so who wants can see it in Wikipedia. The idea of the method is almost the same that is used for drawing dynamic fractals: take some initial value (as usual, here we are talking about complex variables and functions) and apply the formula many times, getting a sequence of numbers. 

Almost always converges to one of the zeros of the function (i.e. the value of the variable at which the function takes the value 0). Halley's method, despite of the complexity of the formula, it is more efficient Newton method: the sequence converges to the zero function faster. 

Fractals in nature 

What do the tree, the sea, clouds or blood vessels we have in hand? There is one property of the structure inherent in all these objects: they are self-similar. From the branches, like a tree trunk, leave the smaller shoots, and from them even smaller, etc., then there is a branch of such tree. In a similar way the circulatory system: arteries arterioles depart, and from them to the smallest capillaries, through which oxygen enters the organs and tissues. 

 

Look at satellite images of the sea coast: we will see the bays and peninsulas; take a look at it, but from a bird's flight: we will see bays and headlands; now imagine that we are standing on the beach and look at their feet: there will always be stones, which jut out into the water than others. That is the coastline when you zoom in it remains similar to itself. This property of the objects of the American (though raised in France) mathematician Benoit Mandelbrot called fractals, and they themselves are objects — fractals.  

With a coastline, but rather, an attempt to measure its length, there is one interesting story that formed the basis of the scientific articles of Mandelbrot and described in his book "the Fractal geometry of nature". We are talking about the experiment that put Lewis Richardson (Lewis Fry Richardson) — a very talented and eccentric mathematician, physicist and meteorologist. One of the areas of his research was an attempt to find a mathematical description of the causes and likelihood of armed conflict between the two countries.  

The number of parameters, which he considered was the length of the common border of two warring countries. When he collected data for numerical experiments, we found that different sources of data on the common border of Spain and Portugal are very different. This led him to the following discovery: the length of borders of the country depends on the line, which we measure. The smaller the scale, the longer it turns out the border. This is due to the fact that at higher magnification it becomes possible to consider all the new curves of the coast that were previously ignored due to the coarseness of the measurements.  

And if with every increase in scale will open not previously taken into account the curves of the lines, it turns out that the length of the boundaries are endless! However, in fact this is not happening — the accuracy of our measurements has a finite limit. This paradox is called the Richardson effect (Richardson effect). 

First 3D render on fractal algorithm 

 

After a few years, Lauren has applied its experience in large-scale project – the animated movie Vol Libre, shown at Siggraph in 1980. This video shocked many, and its Creator was invited to work at Lucasfilm. Here, the animator is able to be realized fully, he created three-dimensional landscapes (an entire planet) for the feature film "Star Trek". Any modern program ("Fractals") or application for creating three-dimensional graphics (Terragen, Vue, Bryce) uses the same algorithm for simulating textures and surfaces.  

In our days 

In our days the theory of fractals finds wide application in various fields of human activities. In addition to painting fractal fractals are used in information theory for compression of graphic data (here mainly used the property of self-similarity of fractals — because to remember is a small fragment of the figure and conversion, by which it is possible to obtain the other parts, and requires much less memory than for storing the whole file). 

Adding to the formula that sets the fractal, random disturbance, it is possible to obtain stochastic fractals, which are very plausible given some real objects — relief elements, the surface of the ponds, some plants that has been successfully used in physics, geography and computer graphics to achieve the greater similarity of the simulated objects with real. In electronics in the last decade has started to produce antennas that have a fractal form. Taking up little space, they provide very high quality signal reception. But economists use the fractal to describe curves, currency fluctuations (this property was opened Mandelbrot more than 30 years ago).