Math Patterns in Nature series: Why the Natural World Looks the Way it Does. #1 SPIRALS
In this #beesteem series I'll introduce you to some fascinating patterns that you can find in nature and art. Those patterns may consist of symmetry, tree structures, spirals, meanders, waves, or stripes. Lot's of possibilities.
Today we will discuss SPIRALS, as they are very well known. Behind the beauty one can find an intriguing mathematical pattern!
What are examples of spirals in nature? Do you recognize these?
(source science magazine )
or
or
or
What is fibonacci or more complex Lucas sequence?
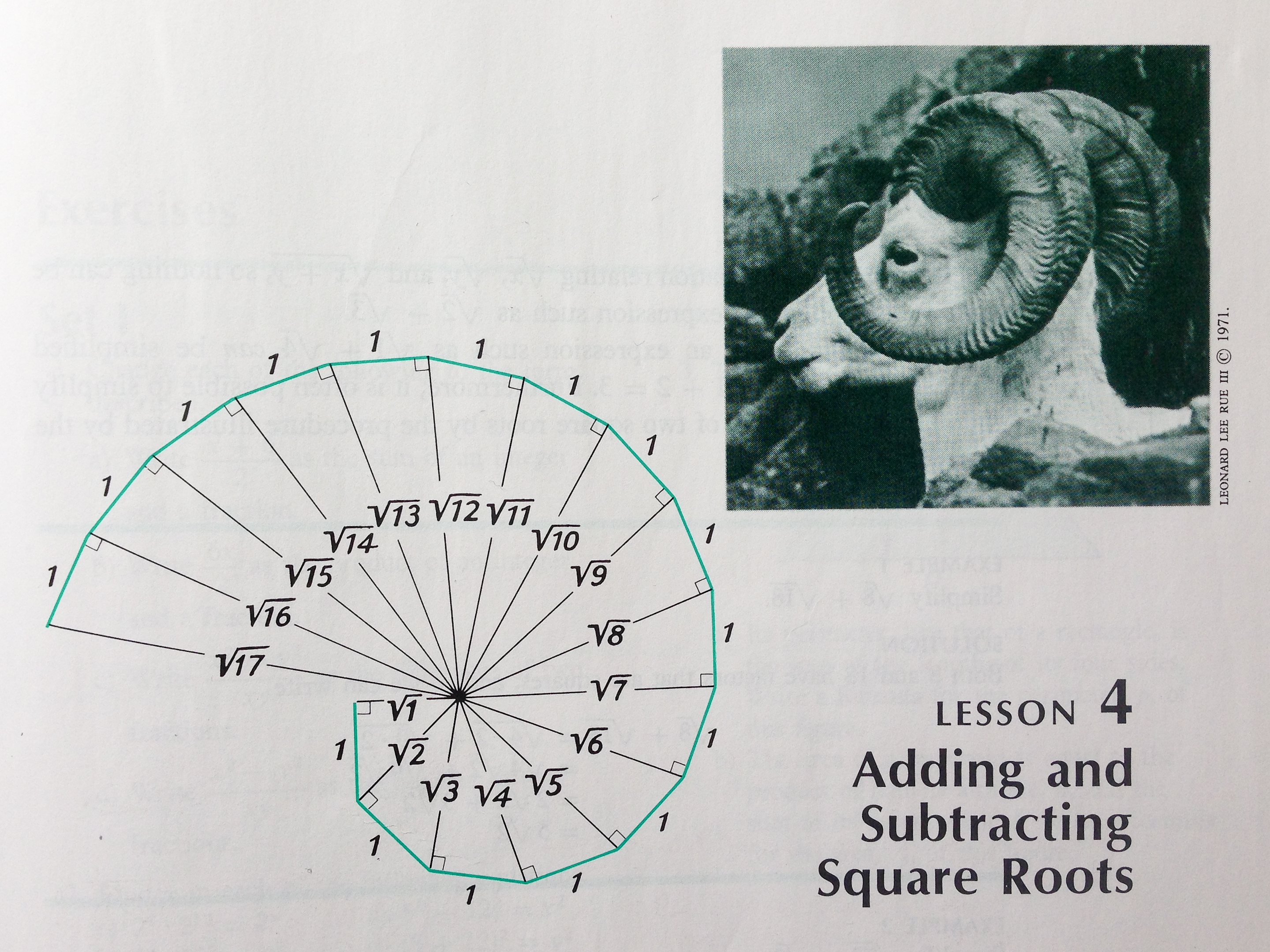
The Fibonacci sequence is the sequence of integers 1,2,3,5,8,13,21,34,55,89,144… in which each member after the second is the sum of the two preceding. The Lucas sequence is the sequence of integers 1,3,4,7,11,18,29,47,76,123… obeying the same rule but with a different starting condition; the F4 sequence is similarly 1,4,5,9,14,23,37,60,97,…. The double Fibonacci sequence 2,4,6,10,16,26,42,68,110,… is double the Fibonacci sequence. We say that a parastichy number which is any of these numbers has Fibonacci structure.
Compare this with the horn structure:
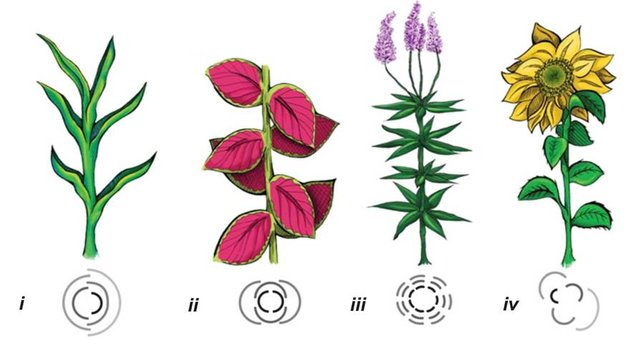
Using a repeating spiral in Leave Ordening
It is interesting to see how the leaves are ordered around the stem, this is called phyllotaxis. It is understandable that the plant wants to get as much sun as possible, so shading is own leaves is not beneficial. Depending on the type of growth several options for the plant are discovered: just one leave at a time, sideways, or spiralling. And in the spirals one again can find varieties of the fibonacci sequence, depending on the angle of rotation (1/2, 1/3, 2/5, 3/8, 5/13 , Fibonacci) These fibonacci fractions describe the angle of windings leaf per leaf.
How to look for Fibonacci sequences in Sunflowers?
the Fibonacci sequence, a set in which each number is the sum of the previous two (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...), found in everything from pineapples to pine cones. In this case, the telltale sign is the number of different seed spirals on the sunflower's face. Count the clockwise and counterclockwise spirals that reach the outer edge, and you'll usually find a pair of numbers from the sequence: 34 and 55, or 55 and 89, or—with very large sunflowers—89 and 144.
Sunflowers are excellent subject for mathematical study. A very recent studyin the Royal Society Journal from 2016 shows that besides fibonacci series, also more complex countings are possible.
http://rsos.royalsocietypublishing.org/content/3/5/160091
When looking at a seedhead such as in the picture below the eye naturally picks out at least one family of parastichies or spirals: in this case, there is a clockwise family highlighted in blue in the image on the right-hand side. When the number of spirals in the family is counted this yields the parastichy number, in this case, 68. The family foliates the seedhead in the sense that every seed in an annular region of the seedhead lies on exactly one member of the family. In this case, as typically, there is another family to be seen, often less obvious to the eye and here highlighted in red and which comprises 42 spirals. These form a (68,42) parastichy pair.
Figure: A double Fibonacci (68,42) example, with 68 clockwise parastichies and 42 anticlockwise ones. (source DOI: 10.1098/rsos.160091)
Hope you found this interesting. See you the next part of this "Mathematical patterns in Nature" where we will focus on another math pattern!
Bee Safe!
@beesteem
Link to other sciencepic post on SEM imaging:
https://steemit.com/sciencepic/@beesteem/sciencepic-small-beasts-magnified-into-big-monsters


_(4308584755).jpg)




Wow. Very informative and nice post!
That is a nice compliment!
@beesteem got you a 16.45% @minnowbooster upgoat, nice! (Image: pixabay.com)
Want a boost? Click here to read more!
just like how the sun moon and stars move along the earth
I recognized it :D
Very interesting.