Calculating the distance of a point and a straight line through orthogonality
Hi everyone:)
Today I want to use orthogonality as a condition to calculate the distance between a straight line and a given point, by getting a parameter value for which we define the length of the vector PxA.
Short definition
The distance between a point "a" and straigth line "g", is the smallest distance from "g" to"a". The illustration below shows it by creating a vector PF that is orthogonal to the straight line. No vector can be shorter than PF, so it is the distance "d",we are trying to find out later.
General approach
If you have got a point a (1/2/3) and want to get the distance to a straight line g with (2/3/1)+ x * (1/0/1), you have to get the points on the line g.
Step 1.
The points on the line g can be calculated by putting in reele numbers into the equation.
Pt (2+x/3/1+x)
Step 2.
We subtract Pt from our point a now:
1 - (2+x) = -1 - x
2 - (3) = -1
3 -(1+x) = 2 - x
Step 3.
From all these vectors we have now, we want to find out the vector with the smallest magnitude.
Using orthogonality
The vector has to be orthogonal to the direction vector of the straigt line g. We can calculate it by using the scalar product/dot product, which has to be zero if we want two orthogonal vectors-> the equation equals 0 (marked in the calculation of Step 2. below)
explanation of the dot product
Step 1.
We mulitplicate our resulte from above with the direction vector of g
(-1 - x) * 1
(-1) * (0)
(2 - x) *(1)
Step2.
This equals:
1*(-1 - x)+ 1*(2 - x)=0
Step3.
Solving the equation gives us:
-1-x +2 -x = 0
1-2x = 0 /-1
-2x=-1 /(-2)
x = 0,5
Step 4.
As we have our result for x now, we put it into the equation of the straight line to find the point on it with the shortest distance to a:
(2/3/1)+ 0,5 * (1/0/1)=
2 + 0,5 = 2,5
3 + 0 = 3
1 + 0,5 = 1,5
P0,5 = (2,5/3/1,5)
Step 5.
As a last step we simply calculated the vector norm, as we are calculating a distance with an certain amount and not just a vector:
/P0,5a/ = √ (2,5 ² +3 ² +1,5 ² ) = √(6,25+9+2,25) ≈ 4,183
For the distance between our line and point, the d on the picture above would be the d ≈ 4,183 we've calculated in Step 5.
Conclusion
We solved the task and can now look on other approaches of fiding out the distance betwen a point and a straight line. Like I mentioned before, you could do it by using extreme values from which you get a function that has a minimum we can find. The minimum would be the shortest distance between the line and the point and would give us the same result as our method did.
Thanks for reading :)
SourceTextErnst Klett Verlag, Lambacher Schweizer Seite 286 ( 1.Auflage) (translated) http://www.mathematik-oberstufe.de/vektoren/a/abstand-punkt-gerade-lfdpkt.html (translated)https://en.wikipedia.org/wiki/Distance_from_a_point_to_a_line
Pictures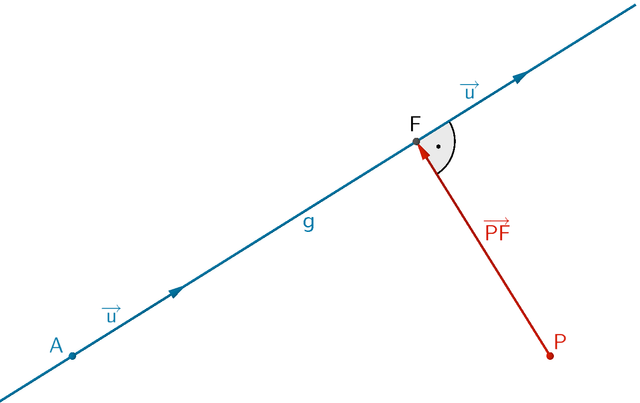

This post has received a 0.63 % upvote from @buildawhale thanks to: @aximot. Send at least 1 SBD to @buildawhale with a post link in the memo field for a portion of the next vote.
To support our daily curation initiative, please vote on my owner, @themarkymark, as a Steem Witness