Learn Basic Python Programming EP.5. - Let's build a Password Strength Analyzer

Let's dive deep into Python, and build an actual useful tool. Yes the previous calculator that we built was pretty useful and nice:
But people mostly use the built-in calculator of the OS, or they do fancy calculations inside a spreadsheet. Unless you have a complex calculation involving arrays and things like that, you probably don't need Python to calculate stuff.
However analyzing the strength of your Password can't be done anywhere else, so for this you do need Python. And you actually want to analyze the strength of your Password, to see how random it is and how strong it is.
There are these websites of course:
BUT YOU SHOULD NEVER EVER WRITE IN YOUR PASSWORD INTO A 3RD PARTY WEBSITE, DON'T BE A FOOL!
So you can't test your Password, there. But this script that we are going to write here is 100% local, doesn't connect to the internet and you can safely check the strength of your Password with this.
Methodology
I am an expert in statistics and time series analysis. And I don't know any better method to test the randomness than to check the autocorrelation function of the bits in the system, together with the skew of the distribution of the bits.
There are many methods:
But some of these are experimental, new or poorly tested. The Chi-Square test is good, but that would be too complex, and I am not going to do that now, but you can check out scipy and figure it out yourself how to use it:
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.mstats.chisquare.html
- https://stackoverflow.com/questions/9330114/chi-squared-test-in-python#9330332
Well we will just compute the skew, since a random data must have a skew of 0, must be uniform, the higher the skew the less random it is. Skew decreases entropy. Like a bad coin that has 20% chance of tails and 80% heads is obviously a bad RNG generator, and has decreased entropy. We will compute Shannon Entropy as well.
Meanwhile the Autocorrelation function measures the correlation between the bits to see if there is any link between the bits. Obviously a random data can't have links. If I remember correctly the threshold is 5%, so if the ACF function value is lower than 0.05 then it's cryptographically secure randomness, and we have to test that down to squareroot(samplesize) orders of lags. Some quants recommend the cuberoot, but I think for safety, especially in longer passwords we can go to the squareroot. So that means that for a Password of 256 bits long Password we take 16 lags and all of them must be under 0.05 significance.
I have already talked about these methods here:
Creating The Password Strength Analyzer
@kskarthik has suggested that I should just paste the code here without the screenshots. Maybe I'll do both, Steemit can't highlight python code so it would be ugly, so I will do both instead.
First of all this is a Python3 script, and I name the file passtest.py. I have also borrowed some code from others on Stackoverflow, but I modified it, so I will source those.
First of all we need to import 4 key libraries, this is a big project, so we can't rely only on the basic code. But all of these libraries should be fully installed in Python3, maybe except Numpy, which you can download here:
import random
import math
import numpy
import os
Then we will rely alot on random number generation, so we will need to seed the RNG from the OS's random pool, I am not sure if I am doing this correctly, since I haven't found a good tutorial about this, but let me know in the comment section.
random.seed(a=os.urandom(512), version=2)
I believe this borrows 512 bytes worth of data from the pool which should be enough. Which is 4096 bits, probably your Password is shorter than this.
Then we borrow a code from Stackexchange, which I have modified mostly:
def autocorrelation(series):
'''
source by Kathirmani Sukumar & Akshay Damle
https://stackoverflow.com/a/20463466/8238271
largely modified by @profitgenerator
'''
n = len(series)
mean = numpy.mean(series)
c0 = numpy.sum((series - mean) ** 2) / float(n)
def r(h):
acf_lag = ((series[:n - h] - mean) * (series[h:] - mean)).sum() / float(n) / c0
return (acf_lag)
cuberoot=math.ceil(n**(1/2))+1
x=[]
for i in range(1,cuberoot): x.append(i)
acf_coeffs = list(map(r, x))
return (acf_coeffs)
This is the autocorrelation function where we insert a numpy array, and this will give back squareroot(samplesize) number of lags with p value of the ACF. If all p values are below 0.05, then the data is securely random.
def skew(array):
skew=0
size=len(array)
for x in range(size):
skew += array[x]
skew/=size
skew=abs(0.5-skew)
return skew
This is the skew function, where we input the numpy array and it will return the skew of the distribution. Ok so far so good, these functions are standalone, now we need to write the parts of the code that does the job.
So far so good, now we ask for the user to input the Password:
Password=input("Enter your Password Here: ")
This is a string, the Password is in string format, and it's visible on the screen, not **** asterisked out, so make sure nobody is watching from behind.
Then we turn the Password from default string format into a segmented bit string, where each character in the Password is represented in it's basic ASCII bit value with this command:
Password_segmented_bitstring= ' '.join('{0:08b}'.format(ord(x), 'b') for x in Password)
So if you Password is Steemit123
If we were to print out this: print (Password_segmented_bitstring)
It would show the bit values of each character:
Each ASCII character is 1 byte (8bit) long composed of binary [0,1]. So you can just lookup the characters here:
And see:
- S = 01010011
- t = 01110100
- e = 01100101
.... - 3 = 00110011
So the binary value matches perfectly. No we need to strip the space from the string:
Password_joined_bitstring=Password_segmented_bitstring.replace(" ", "")
And turn it into a binary array of bits:
Password_bitarray= list(map(int, Password_joined_bitstring))
Then we call the skew function to calculate the skew of the Password:
pbs=skew(Password_bitarray)
Print out the skew:
print ("Skew: "+str(pbs))
Call and print out the autocorrelation values:
print (autocorrelation(Password_bitarray))
Then calculate the Shannon Entropy per bit and the total entropy:
shannon= abs((0.5+pbs) * math.log((0.5+pbs),2) + (0.5-pbs) * math.log((0.5-pbs),2))
print ("entropy per bit: "+ str(shannon))
print ("total entropy: "+ str(shannon*len(Password_bitarray)))
And it's mostly done, now know the characteristics of the Password and it's statistical strength. Now we generate an array of the same size as the bits of the Password, but filled with random data, and check how does our Password's structure compare to Random data:
randarray=[]
for i in range(len(Password_bitarray)): randarray.append( int (round(random.uniform(0, 1) ,0)) )
This structure creates an array and fills it with random, uniform numbers of [0,1]. Now I put a caveat here, because I don't know how good this RNG generation method is. So if you think this is flawed and generates biased numbers please let me know in the comments. But to my knowledge it should be good.
Then we do the same things with this array as well, calculate Skew, Autocorrelation,and Shannon Entropy:
print ("Skew: "+str(rdy))
print (autocorrelation(randarray))
shannon= abs((0.5+rdy) * math.log((0.5+rdy),2) + (0.5-rdy) * math.log((0.5-rdy),2))
print ("entropy per bit: "+ str(shannon))
print ("total entropy: "+ str(shannon*len(randarray)))
This is all of it, now let's do a some cosmetic change, and add my MIT license to the script, after all I wrote the entire code, with the exception of some borrowed code, but even that is edited to suite our needs.
DOWNLOAD THE FULL CODE FROM HERE:
Test
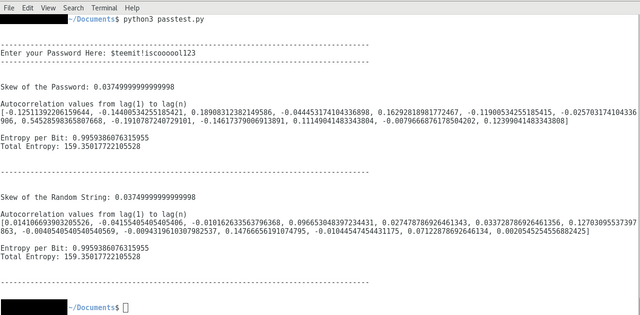
Now let's test it, suppose your Password is: $teemit!iscoooool123
It looks like the skew and the entropy of the Password is the same on the surface, but the autocorrelation values are like 10 times bigger way above the safe threshold, therefore this Password is crap.
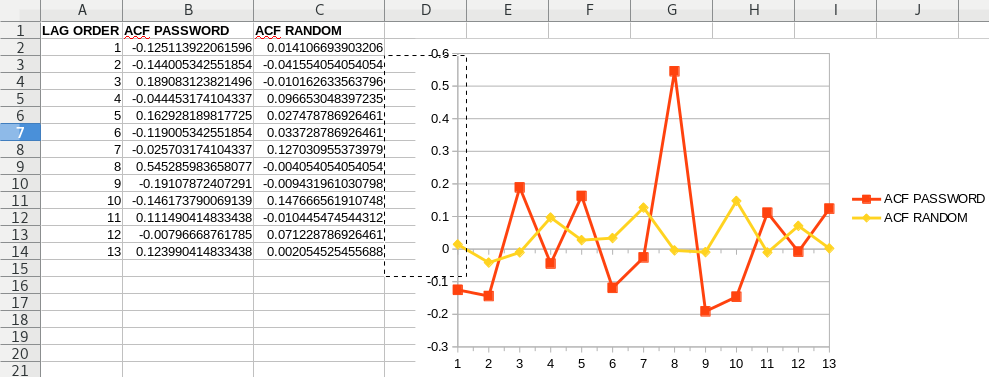
Importing this into LibreOffice, since I have no clue how to use Python GUI:
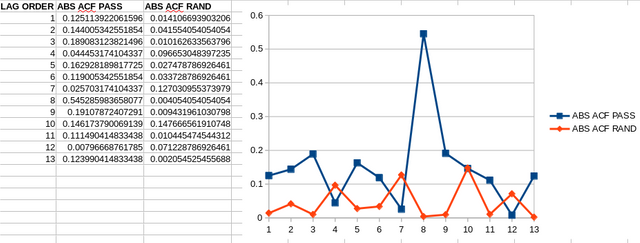
You can see the Random p values are much smaller, and they don't exceed the threshold, meanwhile the Password’s p values do exceed the threshold at lag 8. So this indicates that the randomly generated Password is better than the $teemit!iscoooool123 , much better. It’s perhaps better indicated in the absolute ACF graph:
Conclusion
Now I still don’t know why my random values are not so good, in certain cases exceeding the threshold, maybe I haven’t generated the RNG correctly. Somebody in the comments should point this out if it’s the case.
It would also be interesting to compare this randomness with data from Random.org, maybe their random bits are better, but you probably need to de-skew the data as well, so maybe that is the reason why.
So applying a randomness extractor to the raw uniform random distribution would probably be a good idea:
Other than that I don’t see any other issue. If you do please write in the comment section.
This is a super useful tool, it runs 100% Offline, and you can check the strength of a Password this way.
Disclaimer: Code licensed under MIT license, use this code at your own risk, I will not be responsible for any losses.
Sources:
https://pixabay.com
Python is a trademark of the Python Software Foundation



Too good buddy ☺️ upvoted and resteemed 👍 I am not good at mathematics... But basic programming is pk for me. I have read your other python posts also 😊 steem on 😎