Writing a simple Compiler on my own - Syntax Analysis Theory
Hello it's a me Drifter Programming! Today we continue with my Compiler series to talk about Syntax Analysis! After getting into Lexical Analysis and Symbol Table construction, now what's left is put together those tokens to create some form of grammar! This is exactly the topic of today's post!
So, without further do, let's get started!
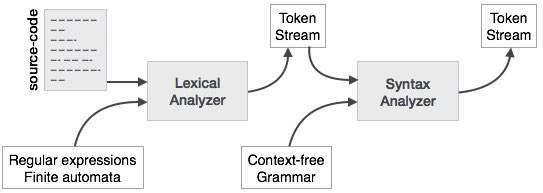
Syntax Analysis
Before getting into grammars we might first want to get into what Syntax analysis is. As the name might already indicate, this step is checking the correctness of the syntax of our program. This means that it combines the tokens from the Lectical analysis to form a syntax tree based on rules, the grammar/production rules.
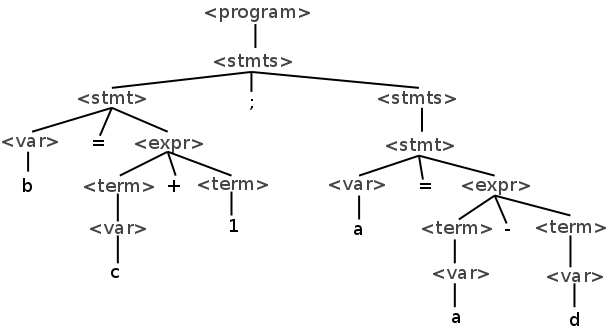
Such a syntax tree might look like this:
You can see that the root is the "root" of our program and it contains statements which are mostly arithmetic expressions.
Of course the traversal of this tree is done with Preorder traversal, which means that we visit the left child, right child and then the parent. That way the parameters of each operation are being read before reading the actual operation that will be applied. So, for an arithmetic expression for example, we first read the numbers on which we will apply their "parent's" operation, which can be addition, substraction etc.
To make our compiler simpler the whole analysis from now on will be based on this exact syntax tree and the syntax analysis of our program. This means that the translation of our program is based on the Syntax. You can clearly see that the intermediate code in form of an Abstract Syntax Tree (AST) is very easily created by simply including only the useful and important nodes of our syntax tree.
Some other things that we also do in this step are:
- Syntax error messages, if the syntax is wrong in some point of the program
- Insert/addup information to our Symbol Table using the information that we get through the Parsing of our program
Syntax Analysis methods and grammars
The Syntax Analysis can be with a deterministic or nondeterministic method.
Deterministic is a method that has only one option to choose in each step. On the other hand Nondeterministic is the method that has multiple choices and chooses one and "goes back" if the option choosen doesn't give a correct answer, until the result is "true" or no more choices can be made to change the "false"-result.
Because some grammars are ambiguous and have more than one interpretations creating a deterministic model/algorithm for our syntax analysis becomes more difficult. That's why we mostly convert ambiguous grammars to non-ambiguous grammars by converting the whole grammar into a equivalent that can be analyzed in a deterministic way or setting one of the choices as the correct one using semantic rules.
Also, the parsing can be done in the directions top-down or bottom-up.
In top-down parsing the Syntax analysis is predicts the following lexical unit or token. On the other hand, bottom-up parsing uses a stack and shifts/reduces into rules depending on the tokens it got inside of the stack.
LL(k) parsing
LL(k) parsing is top-down and checks the tokens following. The simplest grammars can be parsed using a LL(1) grammar, where the one stands for the token lookup count which in this case is one token (the last one). In LL(k) we of course lookup k-tokens. A LL(k) parser only works on non-ambiguous grammars, cause else we have to return to choose another choice instead which takes a lot of time.
In such a grammar we define FIRST and FOLLOW sets and using those we create a parsing table that we use to determine which rule to chose depending on the rule or token that is stored on top of the stack.
You can read more about it here.
LR(k) parsing
Because LL(k) parsing is not working with all the grammars, we choose LR(k) parsers which are bottom-up and use a stack, but in a different way. When shifting we we read the next token and insert it into the head of the stack and when reducing we replace the symbols for an specific rule (right-side) with the non-terminal symbol that represents that rule (left-side).
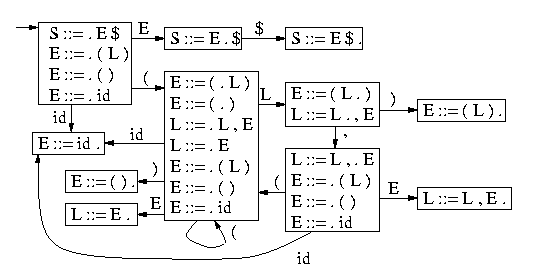
LR(0) is a grammar which doesn't have shift/reduce conflicts and so for a specific symbol we don't have to choose between shifting or reducing, but there is only one. Also, there is only one rule which can be used for the same reduce move and not 2 or more.
So, in such a grammar each state contains the prefixes for the right-sides of the rules that have been recognized in a step of the Syntax analysis.
For example a LR(0) grammar might look like this:
Of course we again define LR(k) parsers which lookup k-tokens. So, you can clearly see that a LR(0) parser doesn't have to lookup a token directly, but can also use the stack only. For most programming languages which are context-free grammars, we define a LR(1) grammar.
Some other useful things are:
- CLOSURE which are the rules to which we can go
- GOTO that is used when we use a rule as a transition (L and E in the picture)
I suggest you to read about those two things and LR parsing in general here.
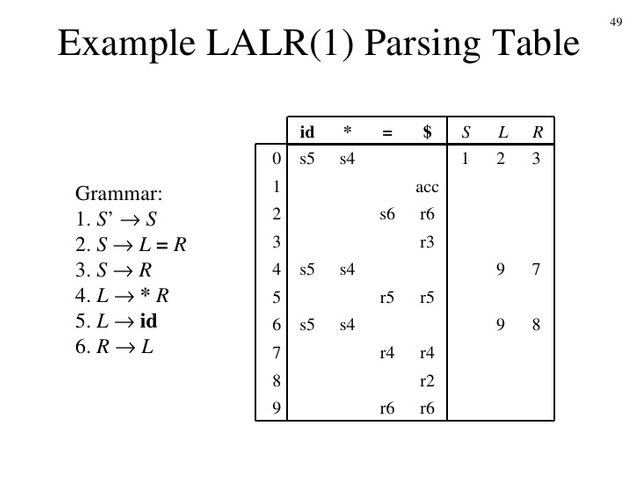
SLR(1) and LALR(1) parsing
In SLR parsing we approximate the solution by getting more efficient results, using the FOLLOW sets of the left-side so that we don't have multiple states that differ only on the lookaheads. This means that SLR(1) is more like LR(0) then LR(1), cause it uses the FOLLOW sets to restrict the number of reduces and so conflicts of LR(0) parsing.
In LALR parsing we don't create states that differ only on the lookaheads. We either add new lookaheads to the LR(1) states and redo the analysis OR create a LR(1) parser and then combine the states that differentiate only on the lookaheads.
The following relation applies:
LR(0) < SLR(1) < LALR(1) < LR(1)
Which means that a grammar of the smaller categories also is a grammar of the greater categories. A grammar that is not in the greater categories is of course not a grammar of the smaller categories!
For example:
A LR(0) grammar is also LALR(1).
A grammar which is not SLR(1) is of course not LALR(1) or even LR(1).
Bison, the C-Tool that I will use for the Syntax and Semantic analysis and actually the rest of our compiler is using a LALR(1) parser! This means that I suggest you to read about LALR(1) parsing and to understand it, cause LR parsers are better then LL parsers. They allow left recurrence and common left orders, and solving conflicts in easier, because we can choose one of the choices and it's mostly done automatically from Bison for us, or we simply have to define Semantic rules!
More about Bison next time...
Image Sources:
Previous posts of the series:
Introduction -> What is a compiler, what you have to know and what you will learn.
A simple C Language -> Simplified C, comparison with C, tokens, basic structure
Lexical Analysis using Flex -> Theory, Regular Expressions, Flex, Lexer
Symbol Table Structure -> Why Symbol Tables and Basic implementation
Using Symbol Table in the Lexer -> Flex and Symbol Table combination
And this is actually it for today and I hope that you enjoyed it!
Next time we will get into Bison and how we write a Parser for our Compiler.
Bye!
Thanks for sharing bro @drifter1 ❤