Thermodynamics Review Problems for Mechanical Engineering Students | Series 8

Hi folks!

This is the 8^th series of my "Thermodynamics Review Problems for Mechanical Engineering Students". If you've missed the previous series you may try scrolling this blog and head over to the "Curriculum". This series features two problems for which both requires us to obtain the rate by which the temperature increases in each substance being used. Without much ado, let's get started in solving these problems.

Review Problem 1

The rate of heat transfer to the surroundings from a person at rest is about 400 kilojoule per hour. Suppose that the ventilation system fails in an auditorium containing 100 people and assuming that the energy goes into the air of volume 1500 cubic meters initially at 300 degree Kelvin and 101 kilopascal, calculate the rate of degree Celsius per minute of air temperature change.

Solution

In solving this review problem, we need to find out what type of thermodynamic process is being applied to the air. Thankfully, the problem states that air is used to cope up the energy that is being transferred by the persons inside the auditorium for the purpose of giving a comfortable ambiance. And when we talk of auditorium, it is a highly maintained and a closed place for which we can say it has a definite volume. With that we will be solving this problem that the air in the auditorium undergoes an isometric process.

Since we have identified that the air inside the auditorium undergoes an isometric process, the very first thing we need to obtain is the total rate of heat transfer for which all the persons inside the auditorium we’re able to give off heat to the surroundings and that is expressed as the product of the total number of persons and the rate of heat that each person gives off. With that we’ve obtained the Total Rate of Heat Transfer (denoted as Q_T in the computation) of the persons inside the auditorium which is equal to 40,000 kilojoule per hour. And since the review problem requires us to have the unit of measurement for time to be expressed in minutes, we will be having the Total Rate of Heat Transfer be expressed in kilojoules per minute which 666.67 kilojoules per minute, as shown in computations below.

Next thing we need to obtain is the mass of air that is circulating inside the auditorium for which we can obtain it using the universal gas constant formula. By doing so, we have obtained the mass of the air circulating inside the auditorium that is equal to 1759.58 kilograms, which was computed during the initial state of air as it enters the auditorium.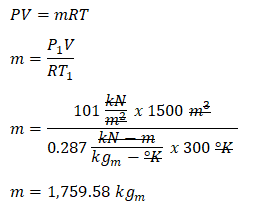


Finally, we can now obtain the rate of temperature change per minute experience by the air as the ventilation systems fail. And we can obtain it using the formula for the heat transferred at constant volume or isometric process. And with that we have obtained the rate of temperature change in degree Celsius per minute which is equal to 0.53 degree Celsius per minute. Also do take note that the specific heat capacity of air at constant volumes is equal to 0.7186 kilojoule per kilogram degree Kelvin and lastly, the change in degree Celsius is always equal to the change in degree Kelvin.

---

Review Problem 2

A fresh poured concrete hardens the chemical transformation and releases energy at a rate of 2 watts per kilogram. Assume the center of poured layer does not have any heat loss and that it has an average heat capacity of 0.9 kilojoule per kilogram per degree Kelvin, find the temperature rise in degree Celsius during one hour of the hardening (curing) process.

Solution

For this review problem since it requires us to compute the temperature rise for which it must be a time rate using hour as the unit of measurement for time, we need to convert the units of power into kilojoule per hour per kilogram first. So the released energy is equal to 7.2 kilojoule per hour per kilogram.

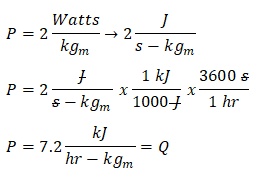
Since the energy that was released upon pouring the fresh concrete is also a form heat, we can now obtain the rate of temperature change for which it is stated in the problem that it rose. We will be using the formula for heat which is expressed as a function of both the specific heat capacity and temperature change. By doing so, we have obtained that temperature rise that is equal to 8 degree Celsius per hour. And I repeat, the change in degree Celsius is just equal to the change in degree Kelvin; similar to the previous problem.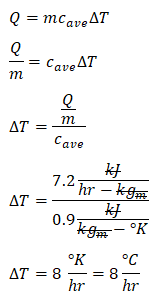

---

Curriculum

• Series 1
• Series 2
• Series 3
• Series 4
• Series 5
• Series 6
• Series 7

Reference

• PIPE - PROBLEM SET #2 by Alcorcon Engineering Review Center

---

<sub>Computations and screenshots are made by the author.

Special thanks to @jbeguna04 for designing the GIF photos.</sub>