Monte Carlo simulation - the best risk analysing method
Monte Carlo method can be defined as a method for simulating random variables with the purpose of calculation the characteristics of their distributions.
The Monte Carlo method have a significant impact on the development of methods of computational mathematics (for example, the development of numerical integration methods) and in solving many problems it can be successfully combined with other computational methods and it even complements them. Its application is justified particularly in those tasks that allow the theoretical probabilistic description. All this is because of getting a natural response with a given probability in probabilistic problems and a substantial simplification of the decision procedure.
Every time in the selection of further action Monte Carlo simulation method gives a possibility to decision maker, to study a range of possible impacts and to assess the probability of their occurrence.
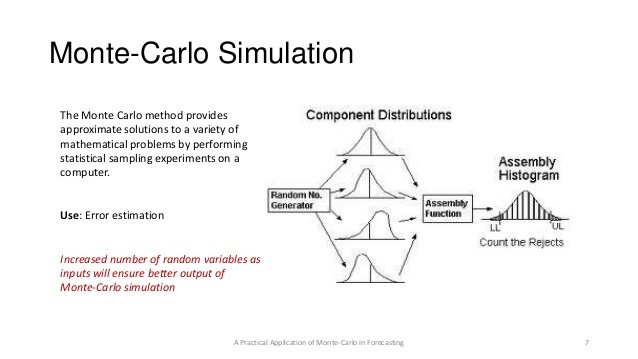
As part of the Monte Carlo simulation method, risk analysis is performed using models of possible results. During the creation of such models any factor which is peculiar uncertainty is replaced by a range of values - the probability distribution. Then multiple calculations of results are performed, each time using a different set of random values of probability functions. Monte Carlo simulation method provides a distribution of values of the possible consequences.
The most common probability distributions are listed below
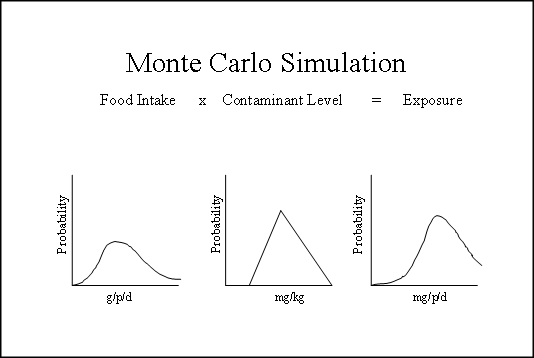
- Normal distribution. is used to describe the deviation from the average, the user defines the average or expected value and standard deviation. Values that are located in the middle, close to the average, are characterized by the highest probability. The normal distribution is symmetric and describes many common phenomena.
Uniform distribution. All values are equally likely to have a certain value; the user simply defines the minimum and maximum. Examples of variables that can have a uniform distribution are production costs or income from future sales of a new product.
Triangular distribution. The minimum, most likely and maximum values are defined. The greatest probability has such values that are located near the point of maximum likelihood.
The lognormal distribution. Values have a positive asymmetry, and in contrast to the normal distribution are asymmetric. This distribution is used to reflect the values that do not fall below zero but can receive unlimited positive values.
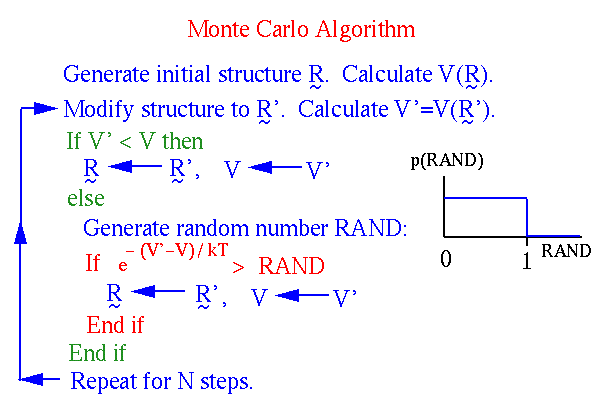
In Monte Carlo simulation method values are chosen randomly from the initial probability distributions. Each sample value is called iteration; results obtained from the sample are recorded. In the process of simulation, such a procedure is carried out hundreds or thousands of times, and the result becomes a probability distribution of possible consequences. Thus, the Monte Carlo simulation method gives a much better idea of the possible events. It gives an indication not only of what can happen but also the probability of such action.
To finish I would like to name the benefits of the Monte Carlo method in comparison with the deterministic analysis:
- Probabilistic results. The results show not only a possible event but also the probability of their occurrence.
- No need to make any assumptions about the symmetry of the distribution laws of input/output variables
- Can be applied even for nonlinear models of observation variables
- Correlation of initial data. The Monte Carlo method can model the interdependent relationship between the original variables.
-The uncertainty of the input quantities may be arbitrarily large
Follow me, to be the first to learn about my publications devoted to popular science and educational topics
With Love,
Kate

Monte Carlo simulations are also the only way for particle physicists to simulate, for instance, LHC collisions (that underlines highly-multidimensional integrals to solve).
This is actually one of the topic I am actively working on for the last 10 years, and we have even a yearly conference called MC4BSM :)
Hi, lemouth.
Monte-Carlo methods are absolutely useful and have many applications. They are also used to calculate multidimensional integrals and in digital filters, e.g. in Particle filter.
MCMC and Bayesian Analysis are really great tools! You can tackle such complex problems that were unthinkable before monte carlo simulations came along. I really enjoyed you description. Do you have an area of application that you work in specifically?
Thank you for the feedback!
First time I faced Monte-Carlo method when I was investigating Bayesian filtering, specifically particle filters.
Included in Steemprentice Spotlight :)
Tweeted by SteemLand
Yea it's good to simulate unknown joint distributions where there are unidentified number of distributions joint together. But if you have 1 distribution, you can just measure the min-max values and extrapolate the probability distribuiton from your sample data.