Intuitive Special Relativity - Time Dilation
In this post I am going to attempt to explain in an intuitive sense the time dilation effect seen in Special Relativity. Let's see how it goes.
But first you may want to read my first two posts leading up to this one.
Intuitive Special Relativity (A Tough Concept Simply Explained)
Intuitive Special Relativity - What Is Time?
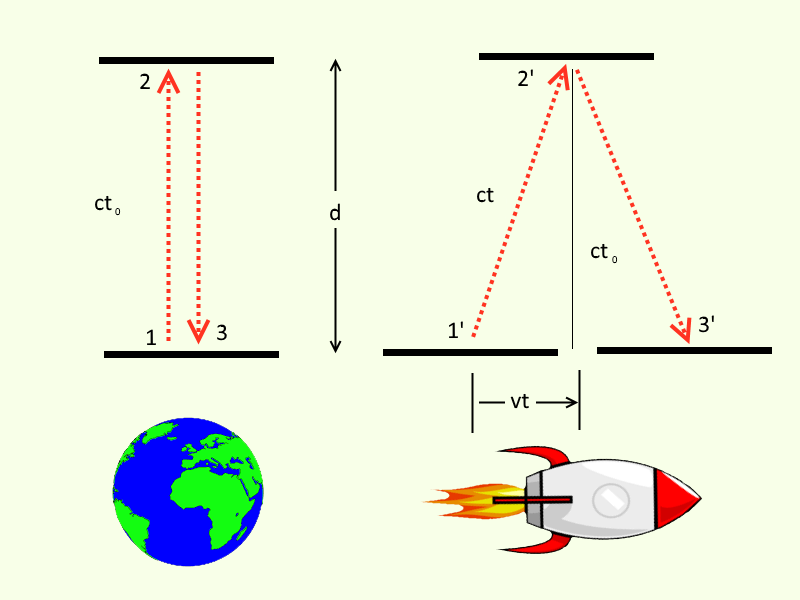
Figure 1. A Simple Time Clock
(Image Credit: Me. with Earth and Rocket icons taken from Pixabay, CC0 creative commons license)
Time dilation means that the time between two events is different for observers moving at different speeds.
It could help to think of time as a 'system effect'. That is, time is not an absolute and it is not really like a river flowing from past to present.
It is better to think of time as particles communicating with one another and that communication is not instantaneous. In fact, we know that the communication cannot travel faster than the speed of light.
The Stationary Observer
Looking at the figure above, the observer on the left is stationary. This observer has made a simple clock that sends a pulse of light up to a mirror and it reflects back down to a detector.
The time to travel up to the mirror is t0 and it is the same time to travel back.
The speed that light moves is 'c', so the distance that the light pulse travels is velocity x time or 2ct0.
The Moving Observer
Again looking at the figure above, the observer on the right is in motion from left to right. This observer also has a simple clock that sends a pulse of light up to a mirror and it reflects back down to a detector.
It is obvious that this second pulse has to travel a farther distance than the pulse for the stationary observer.
Since the speed of light is a constant for all observers, this means that it takes a longer time to be detected.
Math warning
Doing the math, the distance for the moving observer is:
2 x √(v2t2+c2t02) or if you prefer 2(v2t2+c2t02)1/2 which is longer than the stationary observer's distance of 2ct0 for any v > 0.
If the moving observer slows down and stops then v = 0. If you plug v = 0 into the moving observer's equation you get the stationary observer's time.
End of math warning
Discussion
The implications here are:
- The moving observer does not experience time slowing down. To the moving observer everything on the ship, the clocks, computers, chemistry, brain signals all seem to be moving along normally at one second per second.
- The stationary observer looking at the moving observer sees that the moving observer has slowed down. The clock on the space ship moves slower, the astronaut will talk more slowly and he/she will also age more slowly (i.e. slower chemistry).
The Proof
Okay, you may say, so what?
This is just a simple drawing and some simple Pythagorean math.
In fact it is more than just math, there is a massive amount of experimental evidence behind it. Here is one example.
The Muon Half Life
The muon is a particle that is similar to the electron. It has an electric charge of −1 and a spin of 1/2 but with a much greater mass (about 207 times that of the electron).
The muon is unstable and decays into other particles. It has a half-life of about of 2.2 μs (microseconds) when measured at rest in the laboratory.
Here is the evidence for time dilation: Muons are created in the high atmosphere when cosmic rays strike the air.
When created they will have a speed of about 0.99 c.
This means that if time dilation were false, then they would only be able to travel 0.99 x 300,000,000 m/s x 2.2 microseconds = 650m before half of them decay away.
In the next 650 m the remaining half would decay away and so on and so forth.
Since the upper atmosphere is something like 15 km or more from the ground this means almost no muons would survive to reach detectors at the surface of the Earth.
In fact detectors at the surface of the Earth are able to detect substantial levels of muons because time dilation is able to increase their effective half-life (to us stationary observers, to the muons themselves the half-life seems to stay the same).
I will go into the derivation of the Lorentz transformation equations in a later post.
Thanks for taking the time to read my post

It's a dog's breakfast up there really. Lot's of muons, neutrinos, pions and bog standard hadrons.
Taken from (https://physics.aps.org/articles/v9/125)
Get your post resteemed over 90000+ followers and get upto $21+ value Upvote. Your post will skyrocket and give you maximum exposer.
See our all pakages at: https://tinyurl.com/whaleboostup