The science behind music: an evolutionary mistake, and a human obsession

We tend to think of music as a kind of universal language, something that’s been around forever and that everyone can understand. As I wrote about in a previous post, we even sent some of our own music to outer space in the hope that some as-yet-undiscovered alien species might find and appreciate it.
The science of music tells a different story, however. Due to the unique way our bodies and brains work to interpret sound, the likelihood of any other species truly understanding music the way we do is very low. This is not to say that the alien equivalent of Mozart isn’t out there somewhere, writing otherworldly symphonies that are revered by his own people - just that these pieces would, in all likelihood, sound utterly unmusical to a human ear - if we could even hear them at all. The truth is, we humans have a peculiar relationship with sound that allows us to perceive it in an extraordinary way.
Things heard and unheard
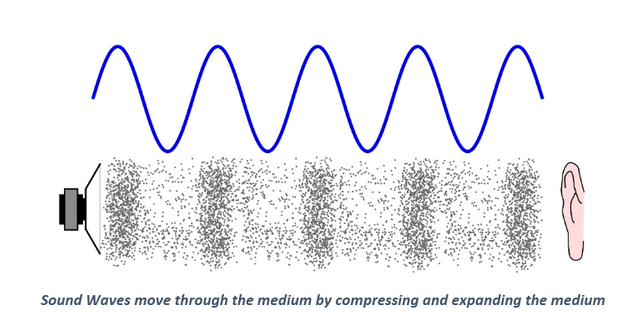
The average adult human can hear sounds at frequencies of between 20Hz and 20kHz. Whales, by comparison, can hear all the way down to 7Hz, or seven wave cycles a second (wave your hand up and down in the air seven times a second and you’ll be creating a sound that they can actually hear!). Dogs, on the other hand, can hear frequencies of up all the way up to 45kHz. Both of these animals perceive a whole range of audible sounds that humans are simply not aware of!
There’s a lot going on within the range of humanly-audible sound, though. In our everyday lives, we’re constantly bombarded with a wide range of frequencies form all kinds of sources. In its natural and disorganised form, this random range of sounds is scientifically referred to as ‘noise’. When refined, organised, and composed, however, these frequencies can be tamed to produce what we know as music.
The architecture of a note
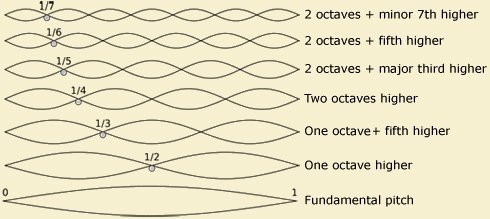
Let’s consider A4, or A above middle C, the grounding point for almost all western music since the early 20th century. This note is usually given the frequency of 440Hz (an essentially arbitrary assignment, but the modern standard), from which the frequencies of all other notes along the scale are calculated. As a pure sine wave at that frequency, A4 is what’s known as a fundamental - a pure tone that has no defining qualities other than its volume and pitch.
Of course, it’s possible to play A4, or any other note, on a wide variety of instruments, and it sounds very different on each. The reason for this is due to the magic of overtones. The diagram above illustrates how the most common overtones, or harmonics, relate to the fundamental wave.
The basic principle is this: when you play A4 on a violin, for example, the foundation, or fundamental of the sound you hear is a sine wave at 440Hz. On top of that, a range of other frequencies are generated as a result of the expression of the player, the corresponding action of the bow and the string, the materials involved in the construction of the instrument, the space in which it’s being played, and many other factors.
These overtone waves interact with each other and with the fundamental to change the quality or timbre of the note in question (without altering its fundamental pitch), which makes the sound recognisable as that of a violin. While any violin can play A4, it’s the difference in the way these overtones interact that sets the sound of a Stradivarius apart from an entry-level plywood-and-superglue model, and, to a greater extent, accounts for the different qualities of sound produced by various instruments.
The magic and mystery of the inner ear
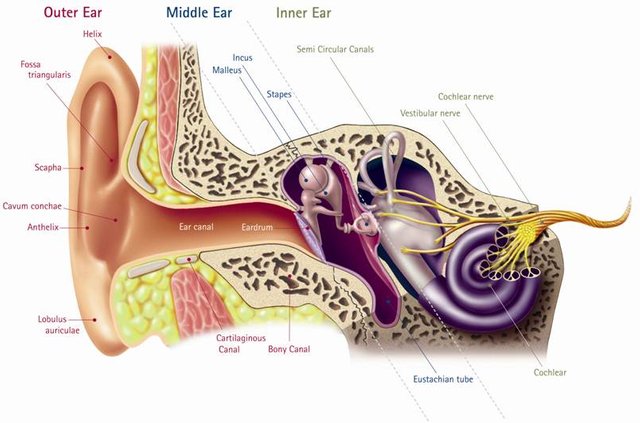
The above image shows the decidedly trippy-looking world of the inner ear. Take a look at the cochlea, the fluid-filled spiral structure to the far right that’s responsible for performing the magical feat of converting audible vibrations into electrical impulses. In short, it achieves this by detecting the point at which a given frequency resonates within this tapering spiral (on account of its wavelength) and sending a corresponding impulse to the brain to register that that frequency has been heard. Mind-blowing stuff!
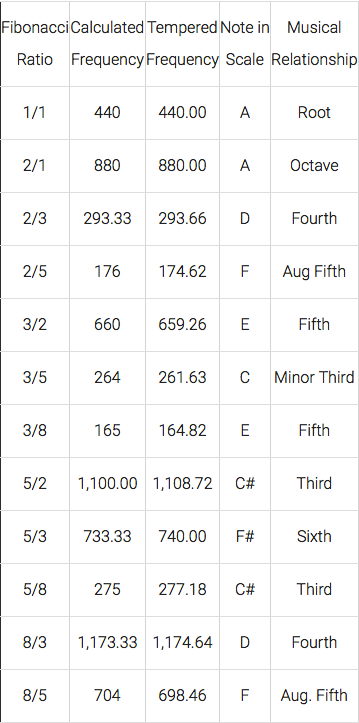
In fact, that’s not just any spiral. The cochlea is an example of what’s known as a Phi spiral, a logarithmic spiral with a growth factor of φ (Phi), commonly known as the Golden Ratio. Related to the Fibonacci sequence (the series of numbers in which each successive number is the sum of the two before it), this ratio has an important role to play in interpreting the audible world, and especially in music.

The relationship between Fibonacci and Phi illustrated
Think of octaves, for example. When you play A4 (440Hz) on an instrument, followed by A5 an octave above it (exactly double the frequency at 880Hz), these notes have a noticeably similar quality, even to the untrained ear, when compared to, say, a B or a C - this despite the fact that one is significantly lower than the other.
The reason for this is that, like the cochlea, the laws of physics that determine the harmonic relationships between notes are also based on the Fibonacci sequence! In this case, the similarity of octaves is due to the fact that two notes an octave apart will resonate at the exact same point of bisection on successive curves of the cochlea itself.
The scale of things

To examine this further, let’s look at the concept of a scale. As we’ve already seen, the ratio between two notes at either end of an octave is exactly 2:1. An octave also comprises thirteen notes a semitone apart from each other, including the root note at either end (A4 and A5, for example). Different groups of eight notes within an octave make up different scales (such as C major, pictured above), and it’s usually the third and the fifth notes in a scale that form the basis of most chords in any given key.
Let’s look at the fifth note in a scale, or the eighth note in an octave. This note is generally known as the ‘dominant’, and can also be expressed in terms of its position within in the octave: 8/13. It’s immediately apparent that these are consecutive Fibonacci numbers. Furthermore, if we divide the numbers above, we get 0.615… very close to Phi itself.
Other Phi-based relationships are found between more complex harmonies as well, which go some way toward explaining why certain combinations of notes sound more pleasant to the ear than others.
The Golden Ratio can be found occurring in nature almost everywhere you look, in everything from the spiralling shape of snail shells to the similar patterns found in the formation of galaxies. Perhaps most interestingly, it also shows up in DNA, which sequences itself in a double helix that follows this ratio very closely for each full cycle.
Evolution’s happiest mistake
The relationship between musical intervals, our ear structure, and Phi helps to explain how we interpret music, but not why. The truth is, it’s very difficult to identify any real evolutionary advantage that music has given the human race, which begs the question of why we evolved it in the first place. A number of theories have been put forward, including:
- The use of music as a show of skill for attracting a mate (as true now as ever)
- As a side-effect of our ancestors learning to synchronise their footsteps (so as to avoid making noise and attracting predators)
- As a prosocial ‘pack-building’ behaviour (similar to the howling of wolves)
- As an ‘emotional language’ (there is even some conjecture that humans hummed or sang before we spoke)
- As a purely cognitive exercise to develop various areas of the brain
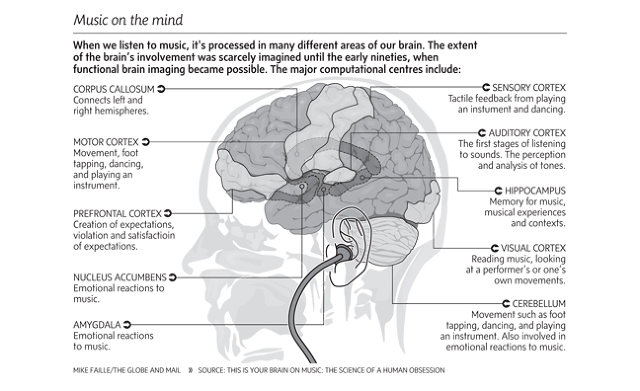
While none are particularly conclusive, there’s no doubt that music does have potentially beneficial effects on the many different areas of the brain that are involved in music, which are neatly summarised below:
Coda
The above information is just a brief introduction to the complex relationship between the laws of physics, the intricacies of the human ear, and the resulting phenomenon that is music. Perhaps the strangest thing of all, however, is that you don’t need to know any of this to understand and appreciate music. It’s an instinctive thing that’s evolved, seemingly out of nowhere, to become an essential feature of our species.
Even stranger is the fact that, needless to say, music has the power to make us feel very deeply - something none of the science described above can really explain. Even if our alien friends were able to discover and hear our music, there’s no guarantee that it would provoke the slightest emotional response - in fact, they might consider us humans to be quite delusional for getting all emotional over mere vibrations.
Whatever the reason, there’s no denying the transcendent beauty and power of music. After all, even Friedrich Nietzsche, one of history’s great cynics (and owner of one of history's great moustaches), was forced to admit the following:

Love your blog , keep on making amazing music blog :)
Or maybe the aliens will be delighted to listen to our music.
Evolution's happy mistake makes the universe a happy place. Just saying :)
It would be pretty strange if they did, but I hope so!
Yup. Let's go with the hope.
Now this is strange. Why is my comment flagged? This kind of act is getting on my nerve now.
Loved your post.
Deepest apologies. Bot gone wild, it has been shut down. I was able to reverse the last two transactions but not these older ones. I have upvoted all your flagged comment on this account to try and make up for it =(
Thank you so much. I was getting irritated with this bot.
I really appreciate your help ( I mean it). Thanks again. Have a great health and success in your life :)
I noticed that! Who knows. I upvoted to cancel it out.
That's very kind. Thank you. I followed you. Will look forward to more awesome work from you. All the best.
awesome post ! very very intesting. i am looking for this kind of interesting content...
Did you know that A is normally not 440 HZ it is 432 HZ. They changed that in 1953. https://1320frequencyshift.wordpress.com/2013/07/01/432-hz-lost-chord-and-new-beam/
Interesting that you point that out. I actually started writing this post with that in mind, but the more I read about it the more it seems that 432Hz, like 440Hz, is essentially arbitrary. There were actually a whole bunch of different frequencies used for A4 before it was standardized to 440Hz. As a musician I sometimes use 432 though, it can sound better on certain instruments.
What do you think, why some intervals (2/3, 3/4, 4/5 ..) are feeling "harmonic" or consonant, but other like tritone (45/32) are dissonant? What is the physiological reason and why humans had got this ability? It is strange that 2/3 sounds better than 45/32. Sometimes tritone is played could be very cool for me.
On the level of vibrations, it has to do mainly with Phi and the way our ear interprets the mathematical relationships between those frequencies. On a psychological level, who knows why we really find one chord more 'pleasant' than another. Of course this can differ between people - I'm also a fan of dissonance a lot of the time!
DInosaur Trombonist!
http://www.sandia.gov/media/dinosaur.htm
Hi! This post has a Flesch-Kincaid grade level of 13.0 and reading ease of 54%. This puts the writing level on par with academic journals.
Sorry but I couldn't agree less, don't you find it a rather odd coincidence that a concert pitch of 432Hz is quarter tone lower than that of 440? Mathematically speaking it exactly opposite, or more precise; in between the half steps of the notes.
Since the anchor note (concert pitch) is based on multiplications, it means it creates a whole spectrum which is not overlapping with that of an anchored note at 440Hz concert pitch!
An analogy of such a spectrum, if you will, is like a comb. Where each frequency is like a tooth of the comb on a logarithmic scale. If you shift the concert pitch, you shift the whole comb to the left or to the right. Does that make sense?
I try to explain it this way because there is so much misinformation on 432Hz.