Equivalence relations

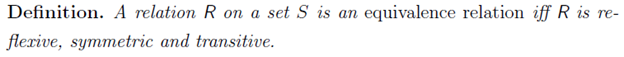
The idea of equivalence relation is not limited to equality (" = "), another interesting equivalence relation is “equivalence mod m” which we will denote using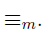

Equivalence mod m

---

This relation is more interesting than actual equality, for it gives us non-trivial equivalence classes. Equivalence classes are one of the most potent ideas in modern mathematics and it’s essential that we understand them.

Let’s consider the following example: “equivalence mod 5”. What other numbers is, for instance, 11 equivalent to?

There are many: any number that leaves the same remainder as 11 when we divide it by 5. This collection of numbers consists the equivalence class of 11 and is denoted by an overline: 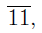, where is defined to be,

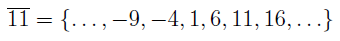
If one replaces the mod 11 with another number, we’ll reach a conclusion that there are, in fact, just 5 different sets that form the equivalence classes.

An example of this set of equalities,

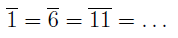
and similarly,

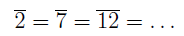
Quotient Structure

---

What we’ve discussed, the mod m, is an example of a quotient structure. One starts with integer and “mod out” by an equivalence relation. What we’ve done is compress the whole 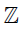(set of integers) elements into a simpler set of five elements. We say, we “move to the quotient”.

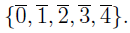
In this act of "moving to the quotient", we lose a lot of information but we have the capacity now to highlight desired features (e.g. properties related to divisibility by 5.)

Equivalence classes

---

The equivalence classes S under the relation R is denoted 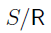(which is read )

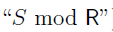The set of equivalence classes forms a partition of the set S.

Partition

---

Partition is an easy way of dissecting sets and equivalence relations give us an easy way of creating partitions (with some added structure). Formally, partition is defined for a set S as:

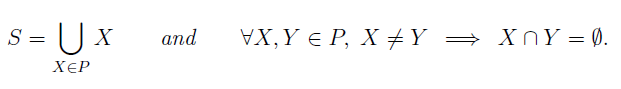
What we need to do to prove that a relation is an equivalence relation is to prove that it is indeed reflexive, symmetric, and transitive.

There exists an equivalence relation that doesn’t satisfy the reflexive, symmetric, and transitive properties of equivalence relations, one example deals with graphs.

Graphs

---

A graph is a mathematical structure consists of two sets, a set of vertices V and a set E of edges. The elements of V maybe have ordered or unordered paired with the elements of E.

1. Directed Graph or Digraph – a graph where E is consists of ordered pairs
2. Undirected Graph – a graph where E is consists of unordered pairs

A few examples of graphs:

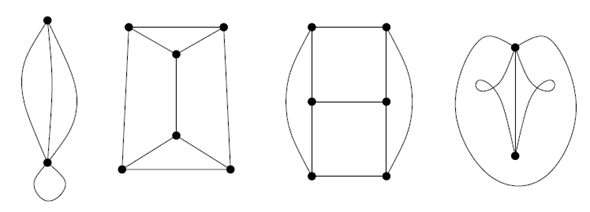
Two graphs are said to be isomorphic if they represent the same connections. The word ‘isomorphic’ means “same shape”. Thus, it is natural to say that two graphs are isomorphic if they have the same shape.

Isomorphism serves as the equivalence relation in graphs.

_{Disclaimer: this is a summary of section 6.3 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.}

---

1. A Gentle Introduction to the Art of Mathematics by Joe Field

---

Thank you for reading ...