Mathematics of Voting Power: Part 2 - Optimizing the total vote value if you can only use an account for a day
In a previous post I derived a convenient formula for the voting value of all votes cast in a single day. In this post I will use this formula to optimise voting output if you can only use an account for a single day.

Suppose that you get to determine all the votes cast of a single account for a single day. Let's also suppose that this account has of the order of 100 000 SP. It is not your account so you will not receive any curation rewards. So you decide that the best way to use this account is to share it with the community by voting for as many posts as possible. In other words, you want to maximise the total voting value of all the votes cast. What kind of strategy should we implement to achieve this?
Assumptions
Let's specify the problem a bit further. I am not going to consider author and curator rewards. So it is only about maximising the total voting output of an account in 24 hours. I will assume that there are enough posts to vote on and that the weight of all the votes is at 100% and that during those 24 hours you will only vote during equal time intervals. Also, I will assume that none of the votes casts are in dust range.
The cost of voting
Intuitively it makes sense to vote for as many posts as possible. But when you do the math it turns out that this gives bad results. Why is this? Voting costs voting power (VP). The value of a vote is equal to some constant number (which depends on account properties) times VP. But the amount of VP that a vote costs is equal to some constant number times VP plus a tiny constant number. This plus another tiny constant number acts as a tiny charge on your VP for casting a vote. If you want to maximise the total casted voting value then you need to pay as few of these tiny charges as possible since these charges reduce your VP, which reduces the total value of your votes cast.
Think of it like this. Suppose you need to get from town A to town B. If you want to go from Town A to Town B you need to cross several bridges. Each bridge requires a toll charge. Then the optimal path to reach town B is to pass as few bridges as possible. And that's why you want to minimise these tiny charges on your VP.
The result
With some calculus you can show that you can maximise the total voting value of this special account if you vote (approximately) every 8.47 min, or equivalently 170 times at equally spaced intervals in 24 hours. Technical details are postponed to the technical appendix below.
Usefull for other scenarios?
So can we use this result to optimise the votes cast of our personal account? Not directly. The VP of the account considered in this post reduces rapidly in the course of 24 hours. When we cast votes we want to ensure that at the beginning of a day we have the same VP as at the end of the day. Let's call this the preservation of VP. So if we want to compute the optimal voting behaviour we need to demand preservation of VP. Again we can use some calculus to obtain an optimal strategy. I will leave this for my next post. :D
Technical appendix
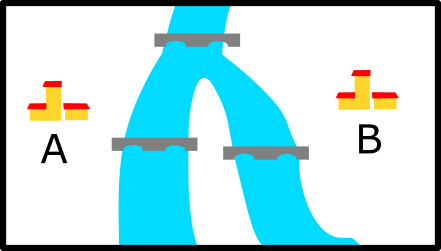
Recall the formula from this post
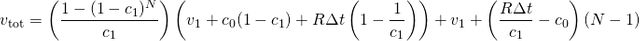
Recall that vtot represents the total value of N-votes cast at equally spaced times in 24 hours. Also recall that R is VP you regenerate per min and Δt is the time interval in minutes between two votes. Then it follows that R Δt = c2 / N . We assume that the starting VP is 100% so we take v1=1. Inserting the constants using the formula sheet we get that c0=49/1000, c1=1/50, c2=1/5.
We are interested in the critical points of vtot with respect to N so we compute
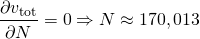
Consequently, vtot has a single critical point. Let's determine what kind of critical point it is:
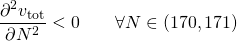
So the critical point is a maximum. N needs to be a whole number. Consequently, we need to evaluate vtot for the value N=170 and N=171 and compare the results. It turns out that vtot is larger for N=170 than for N=171 so N=170 is the optimal value.
Sources: Rewards: formulas from steemit . Top image from Pixabay - Geralt - CC0 creative commons. All equations made using quicklatex it is free. The bridge image made with inkscape which is also free :D
Merchandise :D

There is a MathOwl shop which sells my artsy fartsy stuff. If you got some spare money head over there. You can learn about the colors of pi over here here. I also have really cheap stuff available like these stickers They are an absolute hoot.
Join #steemSTEM
#steemSTEM is a community project with the goal to promote and support Science, Technology, Engineering and Mathematics related content and activities on the STEEM blockchain. If you wish to support the #steemSTEM project you can: Contribute STEM content using the #steemstem tag | Support steemstem authors | Join our curation trail | Join our Discord community | Delegate SP to steemstem
Convenient Delegation Links:
Hmm, I'm trying to reconcile this with my intuition that regardless of how you vote, you cannot assign more vote value over a given time interval (in the steady state, say), because the ratio of (the vote value assigned) to (the amount of time it takes to recover from that vote) is a constant.
Maybe it will come to adding a constraint that the VP is sustainable that this might show up? It is certainly not factoring in recovery time with the current computation, so... Curious to see how that addition affects things.
The strategy in this post is not sustainable. The VP will go down to a couple of percents in the course of the 24 hours. Once you add the sustainable condition the equations will give you what your intuition expects :)
It would be handy to develop a reliable number to express the popularity of a Steemian to predict the anticipated payout per post.
Yes, we could always tabulate their past payouts, to guess their future payouts, but I'm considering a numerical scheme that doesn't require appealing to collecting and fitting data for each and every Steemian.
For example could we find a function of SP, reputation, number of followers, time since last post, number of votes in the last post, and payout of last post.
These seem to be the important attributes, it should just be a matter of fitting a regression. Its probably a linear too so PLS would be reasonable.
Once you have this popularity number this could be included in a voting optimization scheme.
I like this idea!. Indeed a way in which I was made something similar was seeing the bidbots and waiting for someone to pay them in order to vote first... But this was a very Manual action.. not very accurate
Posted using Partiko Android
Nice ideas. I think the value of a post would predominantly depend on the SP of steemians which consistently upvote a specific user. Number of followers on steem seems to be a not so very good predictor of success since you can automise processes without following a user. Another important factor is the tag used. For me there is a great upvote gap between using the steemstem tag and not using this : P
A nice approach u have taken here, I dint think like having only 24hr to use all the SP before. Though the maximum mathematical parts went way over my head, the idea of calculating such a thing is interesting.
Hail the owl of math !
Thankies :D
Thank You very much it helped me a lot @mathowl
Hi @mathowl!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by mathowl from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.