Math art #4: The colors of π
We all know that we can visualise π as half the circumference of a circle of radius one. But there are more cooler ways to to visualise π. Yesterday I made a program which represents the first 10000 decimals of π as a bunch of colourful dots:
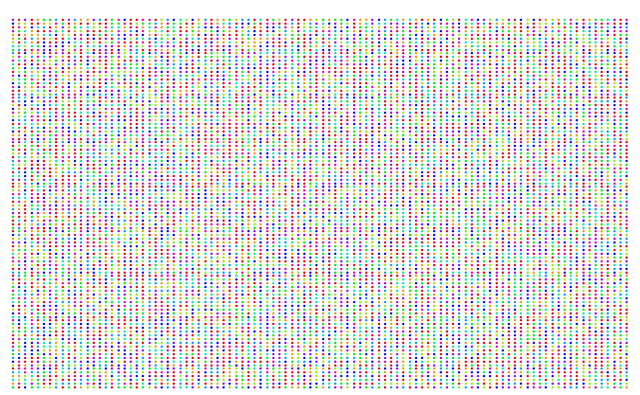
In this post I will explain how this figure was generated and what kind of meaning you can derive from it.
Coloring decimals
The main idea of the program is represting decimals of π as colors. Let's make this more specific.
For now let's just consider two decimals after the dot. So the approximation of of π is given by 3.14. For each decimal I will draw a dot on a vertical line. So in the case of 3.14 I am going to draw three dots, see the picture on the left.
In the above picture on the left I also indicated to which number each dot is connected. I will color these dots using the colourful rules in the list on the left. So then the figure with the three black dots becomes the figure on the right.
If I would consider lots of decimals of π and arrange them in a straight line then I won't get something pretty. So after a certain number of dots (or equivalently a number of decimals) I will continue with a new column of colourful dots. The arrows in the picture below indicate where I position the coloured dots corresponding next (higher) decimal:
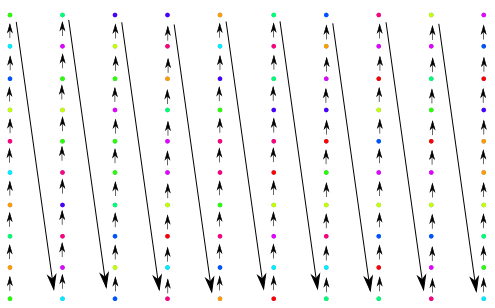
The coloured dots above correspond to the first 100 decimals of π
Let's try another number!
If you would apply this colouring method to a whole number then at some point you will only see one color. For example, for the number 1 all the decimals after the decimal separator are zero; zero corresponds to one color, so eventually you will only see one color. So not very cool. A much cooler number would be 1/7 since its decimals are governed by a repeating pattern: 0.142857142857142857... If you would use the same dot colouring technique then you would get the following picture for the first 10000 decimals:
So you can really see a clear pattern!
The number 1 of course also satisfies a type of pattern since the decimals after the decimal separator are all zero. Numbers which after a given decimal satisfy a pattern are called rational numbers. Numbers which are not rational numbers are called irrational numbers. For irrational numbers there is no pattern present in the decimals. For a more formal definition of rational and irrational numbers you can click here and here [1][2].
Back to the top π figure
Let's go back to the first picture. It indicates that there is no pattern in the first 10 000 decimals of π. So the first 10 000 decimals suggest that π is irrational. The figure does not prove that π is an irrational number since only 10 000 decimals were considered. But it is not too hard to prove that π is an irrational number using basic calculus, see [3] for an easy proof. However, the proof is not as pretty as this post since it does not contain any pretty pictures :)
References
[1] Wolfram - Irrational numbers
[2] Wolfram - Rational numbers
[3] I. Niven, A simple proof that π is irrational, Bull. Amer. Math. Soc. Volume 53, Number 6 (1947), 509.
Pictures/Figures: Everything made with Inkscape (which is a free open source graphics program) and mathematica code. Let me know if you want my notebooks :)
Mathematical owl tax
Join #steemSTEM
#steemSTEM is a community project with the goal to promote and support Science, Technology, Engineering and Mathematics related content and activities on the STEEM blockchain. If you wish to support the #steemSTEM project you can: Contribute STEM content using the #steemstem tag | Support steemstem authors | Join our curation trail | Join our Discord community | Delegate SP to steemstem
Convenient Delegation Links:
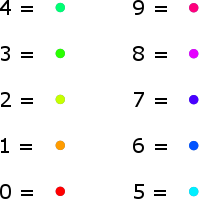


I have never considered this as a possible illustration for irrational numbers! That is cool :)
I totally agree!!!!
Never thought math could be as illustrative and pleasing as this!! Keep it up! Looking forward to more :D
Thanks :)
That is very cool, I think this would look very good on a T-shirt! It looks like you've more-or-less aligned the numbers in spectral order which is also pretty cool!
When I googled today I found many more cooler ways to visualize it -> http://mkweb.bcgsc.ca/pi/art/ and apparently he also used a similar technique to generate the poster for pi day 2013
I’m not a math person
But this is a really cool way of expressing pi
Thanks for the comment and support :)
This is unique! Excellent explanation on the color of π. @mathowl
Things is next level stuff
I don't want to use irrational numbers but my head is telling me... I used to thing pi is just a constant
half the circumference of a circle of radius oneI need when messing with circlesThanks for this @mathowl
Great idea. Now you can run series of articles about visualization of various constants. Like e, φ - there is plenty of those so it will last you for a long time 😛
nah I will write about something completely different again next time :D
So pointless and so cool :)
Maybe this could be a sttemSTEM merchandise?
I think the coolest steemstem merchandise would be a Japanese school girl shouting: Give me your science, steem s(t)em-pai :D
Somehow, my eyes were painful. XD
Always brilliant ideas after next. This really got me read ref [3]. And the date..."simply" proven in 1946 , and stunningly proven through dots in 2018 by mathowl! power💪
Thanks for the support. Well I didn't really prove anything in this post. The dots don't say anything about wheter pi is an irrational number
aw!.. o my... I mean stunningly presented through dots... sorry🙊